为什么方差的分母常常是n-1
# 为什么方差的分母常常是$n-1$?
Tags: #Math/Statistics #Variance
按照定义, 方差的分母的确应该是$n$
但是因为我们用样本的均值$\overline X$代替了数学期望$\mu$, 而这个$\overline X$是有误差的, $\frac 1 n \rightarrow \frac 1 {(n-1)}$是为了消除这个误差.
# 详细解释
前提： $X_i$ 相互独立
按照定义, 方差的公式是: $$\sigma^{2}=\mathbb E\left(\frac{1}{n} \sum_{i=1}^{n}\left(X_{i}-\mu \right)^{2}\right)$$ 其中, $\mu$是随机变量的数学期望.
- $$\frac{1}{n} \sum_{i=1}^{n}\left(X_{i}-\mu \right)^{2}$$是方差的无偏估计
但是, 实际工作中, 样本的数学期望常常难以得到 ,所以我们用样本的均值来代替数学期望: $$\mu \rightarrow \overline X = \frac{1}{n} \sum_{i=1}^{n} X_{i}$$
这会不会带来误差呢? 当然会!
- 如果直接采用$\frac{1}{n} \sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2}$ 作为估计，那么你会倾向于低估方差! (变成偏低的有偏估计)
这是因为: $$\begin{aligned} \frac{1}{n} \sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2} &=\frac{1}{n} \sum_{i=1}^{n}\left[\left(X_{i}-\mu\right)+(\mu-\bar{X})\right]^{2} \\ &=\frac{1}{n} \sum_{i=1}^{n}\left(X_{i}-\mu\right)^{2}+\frac{2}{n} \sum_{i=1}^{n}\left(X_{i}-\mu\right)(\mu-\bar{X})+\frac{1}{n} \sum_{i=1}^{n}(\mu-\bar{X})^{2} \\ &=\frac{1}{n} \sum_{i=1}^{n}\left(X_{i}-\mu\right)^{2}+2(\bar{X}-\mu)(\mu-\bar{X})+(\mu-\bar{X})^{2} \\ &=\frac{1}{n} \sum_{i=1}^{n}\left(X_{i}-\mu\right)^{2}-(\mu-\bar{X})^{2} \end{aligned}$$
换言之，除非正好 $X=\mu$, 否则我们一定有 $$\frac{1}{n} \sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2}<\sigma^2$$
而 （证明见 Prove that $E (\overline{X} - \mu)^2 = \frac{1}{n}\sigma^2$）： $$\mathrm{E}\left[(\bar{X}-\mu)^{2}\right]=\frac{1}{n} \sigma^{2}$$
所以:
$$E\left[\frac{1}{n} \sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2}\right]=\sigma^{2}-\frac{1}{n} \sigma^{2}=\frac{n-1}{n} \sigma^{2}$$
为了调整, 我们乘上$\frac n {n-1}$
公式也随之变为: $$ \frac n {n-1} \times \frac{1}{n} \sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2} = \frac{1}{n-1} \sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2} $$
%% 下面这个说法好像有点问题, 问题的关键是直接代换会使方差的估计变成有偏估计
我们看以下例子:
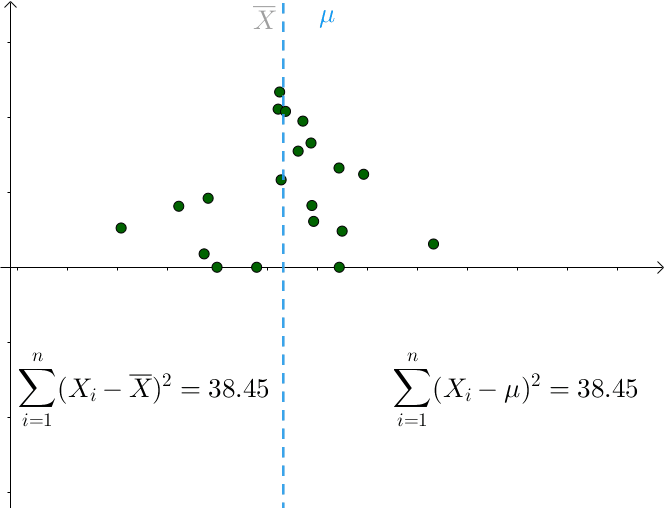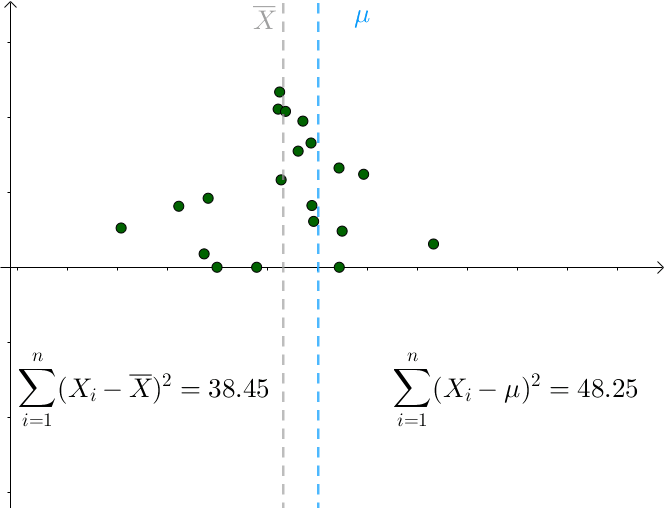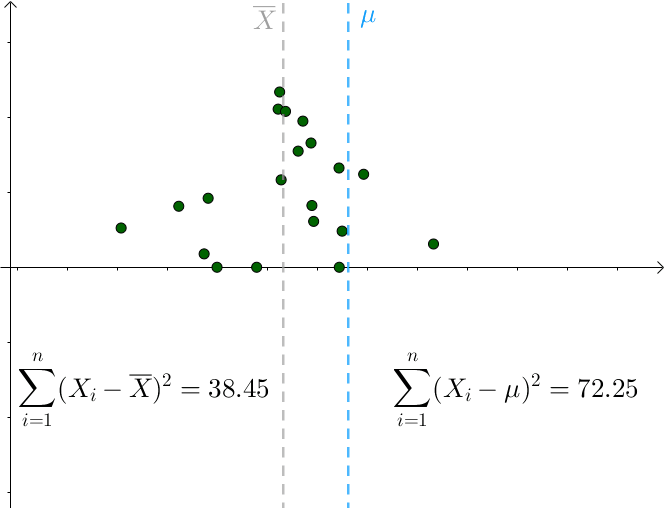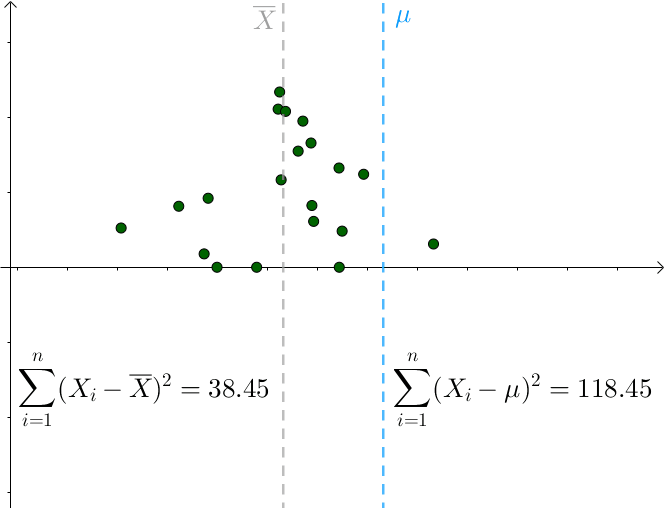图中, 绿色散点是样本. 对于可能的真实分布, 我们取不同的$\mu$, 可以看到, $\mu$与$\overline X$的距离越大, 方差的误差也越大%%