Compiler-3_算符优先分析
# Operator-precedence grammar
Tags: #Compiler #Course #FormalLanguage
# 算符优先文法
算符优先文法(OPG)是一种有特殊性质的上下文无关文法(CFG)
它的特殊性质表现为:
- 产生式右部不能为空 (即没有 $P\rightarrow \varepsilon$)
- 产生式右边不能有两个连续的非终结符 (即没有 $P\rightarrow \cdots AB\cdots$)
上述规则使得我们可以定义终结符之间的"优先级"(Precedence), ( 为什么?)
算符优先分析不是规范规约, 它的每一步不一定替换句柄
在书里面的定义中, 算符文法是不含两个连续非终结符的文法, 算符优先文法则是终结符之间最多只有一种优先关系的算符文法
# Main differences with respect to LR parsers
- There is no explicit state associated to the parser (and thus no state pushed on the stack)
- The decision of whether to shift or reduce is taken based solely on the symbol on the top of the stack and the next input symbol (and stored in a shift-reduce table)
- In case of reduction, the handle is the longest sequence at the top of stack matching the RHS of a rule
# 算符优先文法的核心特征
有几个概念我感到很难理解:
- 为什么算符优先文法要叫"算符优先"文法? 如果是因为它定义了运算符之间的优先级, 那么:
- 运算符的优先级怎样帮助我们进行语法分析?
- 为什么"产生式没有两个连续的终结符"便可以定义运算符之间的优先级? 如果有了两个连续的终结符又会怎样干扰算符优先分析的正确进行?
- 算符优先分析法是仿效四则运算的计算过程而构造的一种语法分析方法。算符优先分析法的关键是比较两个相继出现的终结符的优先级而决定应采取的动作。1
- “仿效四则运算的计算过程” - 何以见得?
总之, 算符优先分析的核心概念还是像一团难以捉摸的雾
仿照四则运算可否这样理解:
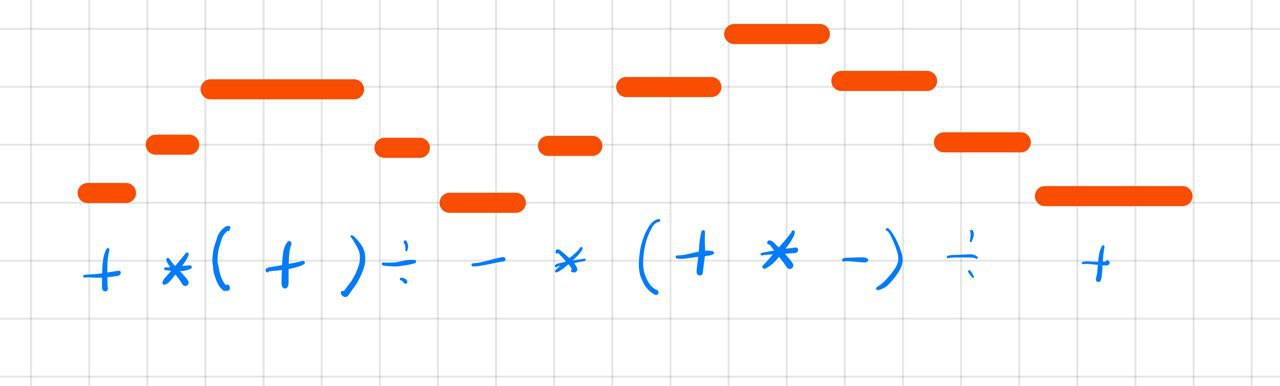
Oberlin University的PPT2为我们提供了一种新的思路:
我们首先定义"括号文法(parenthesis grammar)":
- a) The right hand side of every rule is enclosed in parentheses.
- b) Parentheses occur nowhere else.
- c) No two rules have the same right hand side.

- The parentheses make the prime phrases disjoint. The handle is always the leftmost prime phrase.
那么我们可以这样理解优先级文法:
- Def. A simple precedence grammar is one in which we can insert symbols “<”, “=”, and “>” to produce a language (treating “<” and “>” as parentheses) that can be parsed like a parenthesized grammar.
一个"优先级文法"产生的句子是一串嵌套的括号.
一个素短语便是一对括号, 我们不断消除最左边的素短语, 暴露下面的(栈里面的)素短语
嵌套的"越深"的括号"堆的越高", 我们parse的过程便是不断让这个山变矮的过程.

理解"句子括号": We always start with “<” and the first token on the stack, and at EOF push “>”. We should end with the Start symbol on the stack.
理解算符文法: 关于为什么没有两个连续非终结符, 便可以称之为"算符文法",我实在找不到更详细的资料了, 下面那篇论文里面的这段话似乎是其最初的定义:
 注意这个性质; 如果产生式里面没有两个连续的非终结符, 那么任意句型里面也不可能有两个连续的非终结符:
注意这个性质; 如果产生式里面没有两个连续的非终结符, 那么任意句型里面也不可能有两个连续的非终结符:证明:
 我猜测因为因为算术表达式里面都是算子和算符交替出现, 所以会有"算符文法"这个名字.
我猜测因为因为算术表达式里面都是算子和算符交替出现, 所以会有"算符文法"这个名字.
综上, 结合"算符"文法和"优先级"文法, 便有了"算符优先文法"
# History
Robert W. Floyd. 1963. Syntactic Analysis and Operator Precedence. J. ACM 10, 3 (July 1963), 316–333. DOI:https://doi.org/10.1145/321172.321179
没有细致的考证过出处, 只是谷歌搜索到的, 但是根据文章内容猜测应当是出处.
在文章里面, 我理解到了以下概念:
- 理解"素短语":
- A prime phrase is a phrase which contains at least one terminal character, but no prime phrase other than itself.
- 素短语里面的"素", 指代的是Prime, 也就是素数的"素", 应当理解为"最基本的, 最原初的", 因为素数是"最小不可分的数"(算术基本定理3)
- 理解课本里面的"句子括号: #"4
- 对于 $BxC$, 其中B, C为终结符
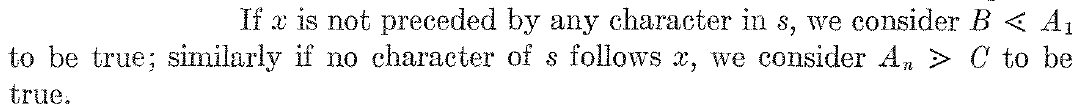
- 像上面这样记忆其实比"把#当作一个终结符"简单
- 对于 $BxC$, 其中B, C为终结符
# 算符优先级
a ⋖ b This means a “yields precedence to” b.
a ⋗ b This means a “takes precedence over” b.
a ≐ b This means a “has same precedence as” b.
# 怎么确定优先级
a等于b 当且仅当 文法G中含有形如$P→ \cdots ab\cdots$ 或 $P→\cdots aQb\cdots$的产生式;
a小于b 当且仅当 G中含有形如$P→\cdots aR\cdots$ 的产生式,而$R \overset{+}{\Rightarrow}b\cdots$ 或$R\overset{+}{\Rightarrow}Qb\cdots$ 即语法树中, a在b的左上面
a大于b 当且仅当 G中含有形如$P→\cdots Rb\cdots$ 的产生式,而$R\overset{+}{\Rightarrow}\cdots a$或$R\overset{+}{\Rightarrow}\cdots aQ$ 即语法树中, a在b的左下面
在算符优先文法里面, 任意两个终结符 至多满足一种关系
# 分析步骤
 前三步都是在进行准备工作, 即构造后面要用到的算符优先表,
同时, 确定优先级的过程也是验证这个文法是不是算符优先文法的过程
前三步都是在进行准备工作, 即构造后面要用到的算符优先表,
同时, 确定优先级的过程也是验证这个文法是不是算符优先文法的过程
# 检查是否有ε-产生式
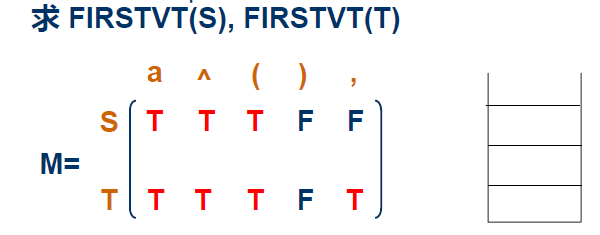
# FIRSTVT(NT), LASTVT(NT)
- 构造对象: 所有非终结符
- 定义: $$\begin{aligned} &\operatorname{FIRSTVT}(\mathrm{P})=\left{\mathrm{a} \mid \mathrm{P} \stackrel{+}{\Rightarrow} \mathrm{a} \cdots \text { 或 }{\mathrm{P}} \stackrel{+}{\Rightarrow} \mathrm{Qa}\cdots , \mathrm{a} \in \mathrm{V}{\mathrm{T}} \text { 而 } \mathrm{Q} \in \mathrm{V}{\mathrm{N}}\right} \\ &\mathrm{LASTVT}(\mathrm{P})=\left{\mathrm{a} \mid \mathrm{P} \stackrel{+}{\Rightarrow} \cdots \mathrm{a} \text { 或 } \mathrm{P} \stackrel{+}{\Rightarrow} \cdots \mathrm{aQ}, \mathrm{a} \in \mathrm{V}{\mathrm{T}} \text { 而 } \mathrm{Q} \in \mathrm{V}{\mathrm{N}}\right} \end{aligned}$$
- FIRSTVT: 非终结符的所有第一个(FIRST)终结符(VT)
- LASTVT: 非终结符的所有最后一个(LAST)终结符(VT)
# 如何构造 FIRSTVT(NT), LASTVT(NT)
- 递归构造
# FIRSTVT(B)
- 首先所有产生式$B→a\cdots$, 或者 $B→Ca\cdots$, 有 $a\in FIRSTVT(B)$
- 然后对于所有的$B→Ca\cdots$, 有$FIRSTVT(B) = FIRSTVT(C)\cup FIRSTVT(B)$
这样的话可能会套很多层, 书上采用的方法是用一个栈:

- 首先, 将直接能够看出来的元素在表中标记, 并且入栈.
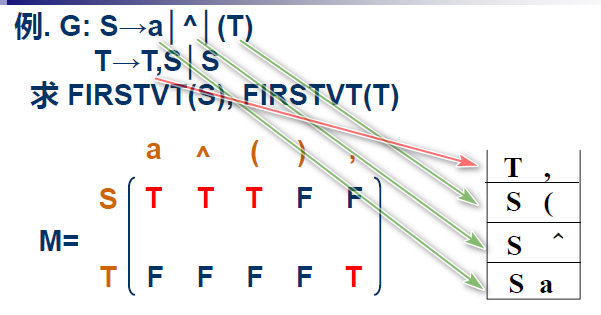
- 然后, 将栈顶元素$(C, d)$出栈, 如果C是某一个产生式的第一个非终结符(比如$B→Ca\cdots$), 那么将$d$加入到$FIRSTVT(B)$里面.
- 标记$(B, d)$, 同时$(B, d)$入栈
- 重复, 直到栈空
理解FIRSTVT(B)
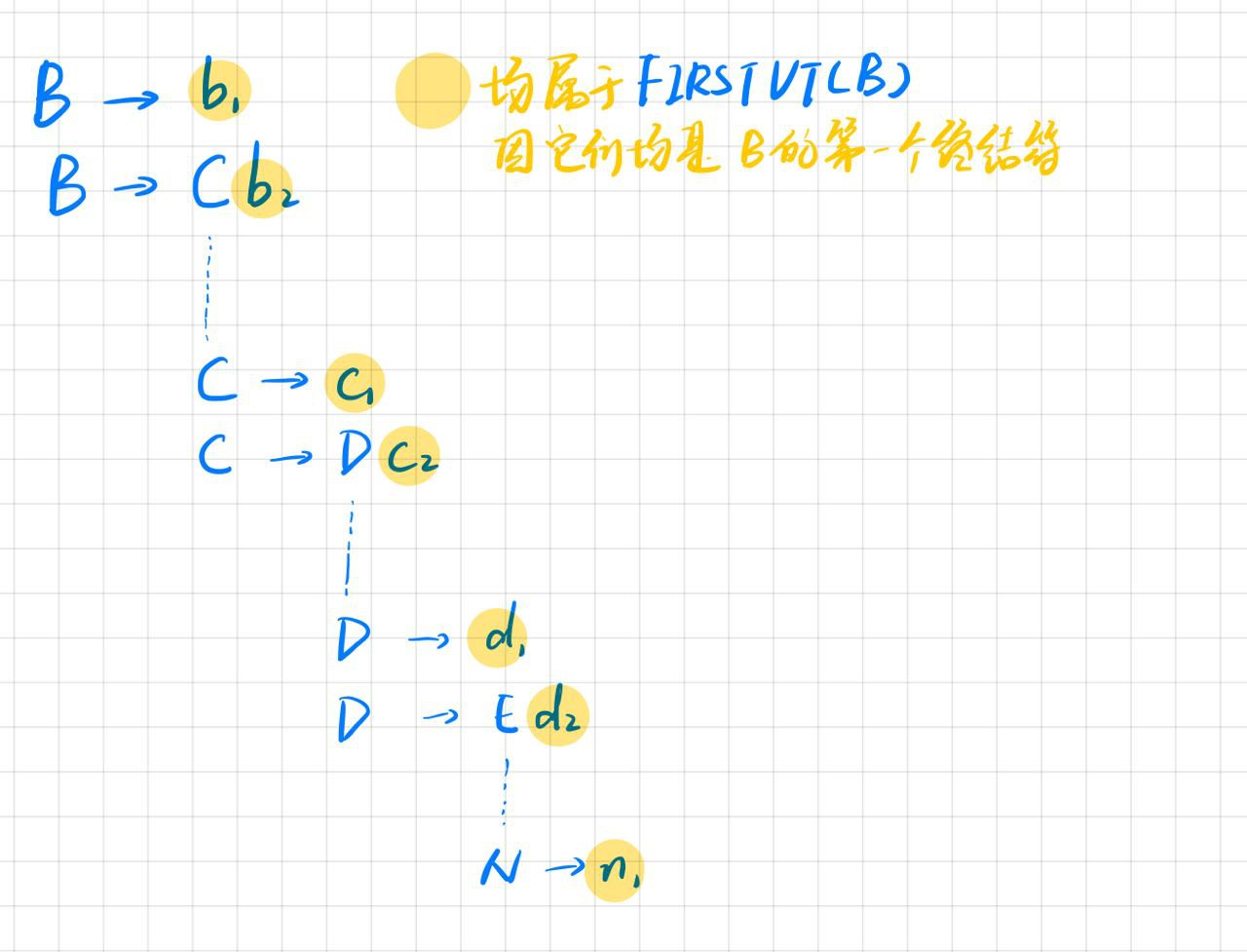 理解这种"栈中元素对"的更新方式
理解这种"栈中元素对"的更新方式
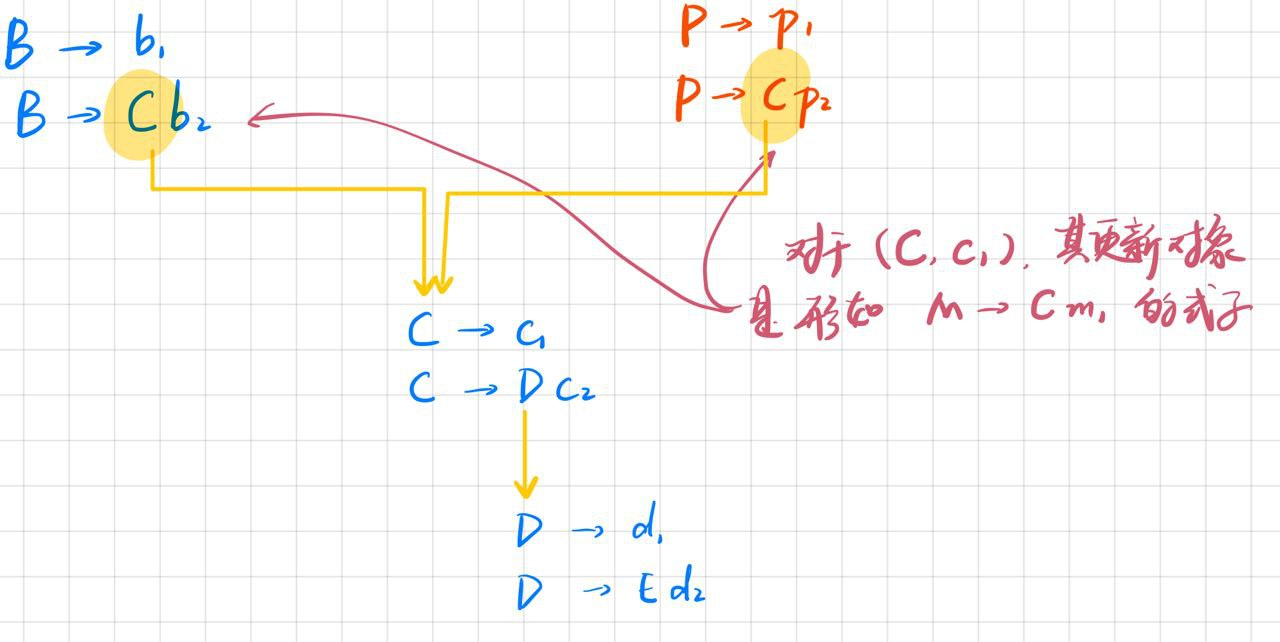
# LASTVT(B)
类似的
- 首先所有产生式$B→\cdots a$, 或者 $B→\cdots aC$, 有 $a\in LASTVT(B)$
- 然后对于所有的$B→\cdots aC$, 有$LASTVT(B) = LASTVT(C)\cup LASTVT(B)$
# 构造优先级表
注意区分: 这个表是构造FIRSTVT 和 LASTVT 的, 不是优先级表
然后我们根据FIRSTVT 和 LASTVT 来构造优先级表

 构造出来长这样
构造出来长这样
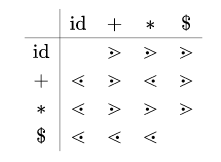
# 特别注意!
算符优先级不满足交换律, 所以$a\lessdot b\nRightarrow b\gtrdot a$
所以这个表格并不是反对称矩阵!!
要分清横纵轴, 在课本和课件里面, 都是

课本里我们引入#符号表示句子的括号 即一开始 在文法中添加E→#E# , E为开始符号, 容易推出:
- # ⋖ FIRSTVT(E)
- LASTVT(E) ⋗ #
- # ≐ # %%>
%%
课件里面没有写, 但是在分析具体的句型的时候需要记住
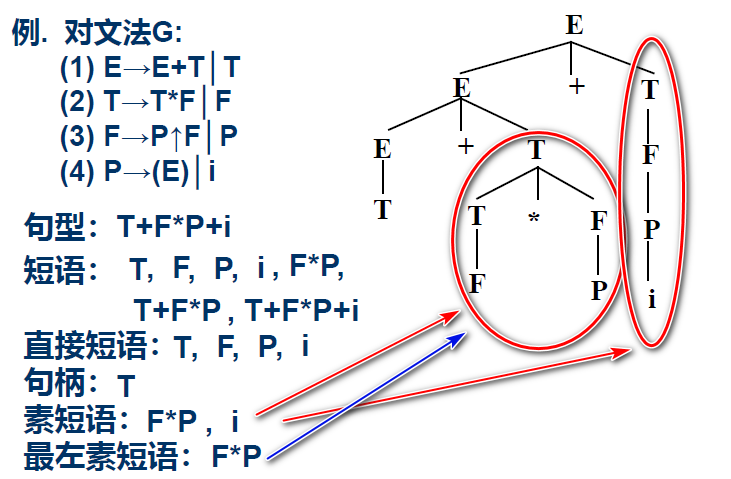
# 最左素短语—算符优先分析中的可归约串
- 素短语 至少含有一个终结符且除它自身之外不含有任何更小的素短语。 (语法分析树里面至少含有一个终结符的最小子树)
- 最左素短语
处于句型最左边的那个素短语。
 在算符优先句型里面, 句型一定是以下格式:
$#N_1\space a_1\space N_2\space a_2\space \cdots N_n\space a_n\space N_{n+1} #$
其中: ${a}{{i}} \in {V}{{T}}, {N}{{i}} \in {V}{{N}}$ (非终结符可有可无, 但是一定不会挨着)
在算符优先句型里面, 句型一定是以下格式:
$#N_1\space a_1\space N_2\space a_2\space \cdots N_n\space a_n\space N_{n+1} #$
其中: ${a}{{i}} \in {V}{{T}}, {N}{{i}} \in {V}{{N}}$ (非终结符可有可无, 但是一定不会挨着)
句型是这种形式是算符文法的定义造成的, 算符文法不允许出现两个连续的非终结符.
一个例子:
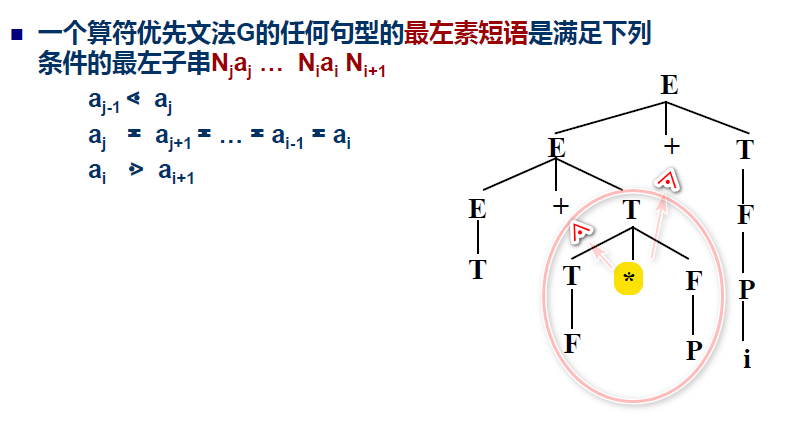 直观上这样理解:
直观上这样理解:
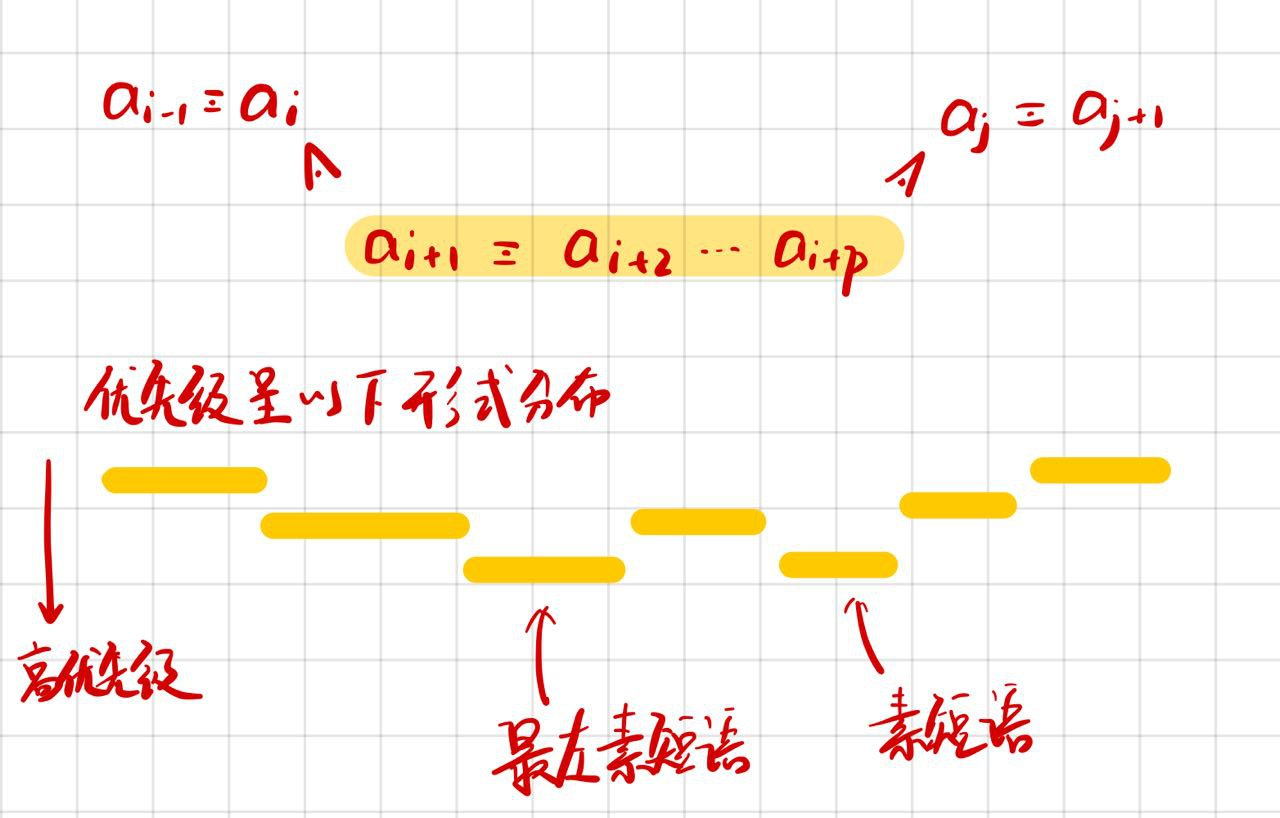
# Start Parsing!
算符优先算法 解析 一个具体的例子: Operator_Precedence_Parse
需要注意的是:
- 算符优先分析在规约这一步上面, 得到的是"某个非终结符N", 这个非终结符是不重要的, 这在下图中可以清晰的看出:
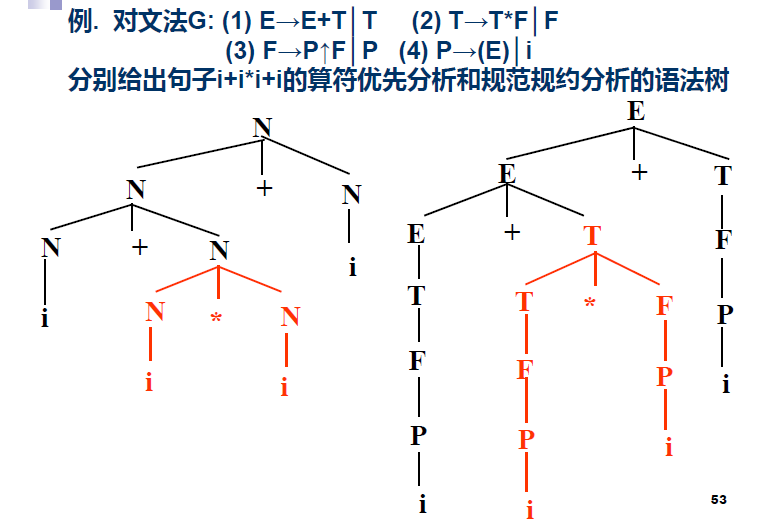
- 上图同时说明了 算符优先分析不等价于规范归约,未必是严格的最左归约(从树里面可以看出省略了一些步骤, 即跳过了所有单非产生式所对应的归约步骤), 所以归约速度快,但容易误判(因为忽略非终结符在归约过程中的作用,存在某种危险性,可能导致把本来不是句子的输入串误认为是句子)
- 这也同时说明了算符优先分析没有"状态(State)“一说, 即没有状态入栈, 推导过程完全凭借栈顶终结符与下一个终结符
易错:
- 优先级关系是每一步都有的

- 我的:
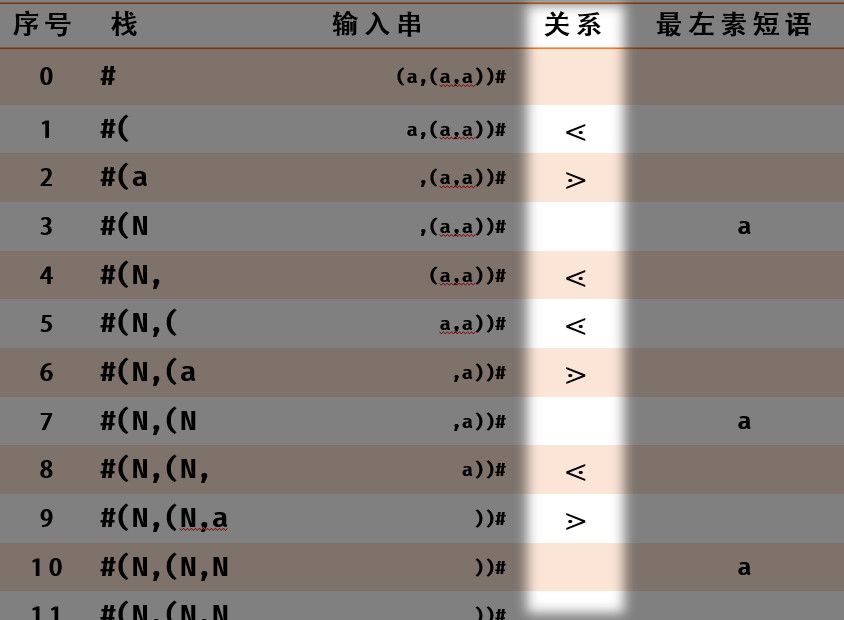
# 优先函数
实际应用中, 考虑到存储优先表的开销太大, 我们常常用优先函数代替优先表:
函数f 称为入栈优先函数, g 称为比较优先函数
- 若 $\theta_{1}⋖\theta_{2}\quad$ 则 $\quad f(\theta_1)<g(\theta_2)$
- 若 $\theta_{1}≐\theta_{2}\quad$ 则 $\quad f(\theta_{1})=g(\theta_2)$
- 若 $\theta_{1}⋗\theta_{2}\quad$ 则 $\quad f(\theta_{1})>g(\theta_{2})$
注意:
- 不是每一个优先表都有对应的优先函数
- 原来优先表为空的项(不存在优先关系的终结符对), 转化为优先函数以后, 与自然数相对应,变成可以比较的。所以要进行一些特殊的判断
- 优先函数不唯一,只要存在一对,必存在无穷对优先函数。

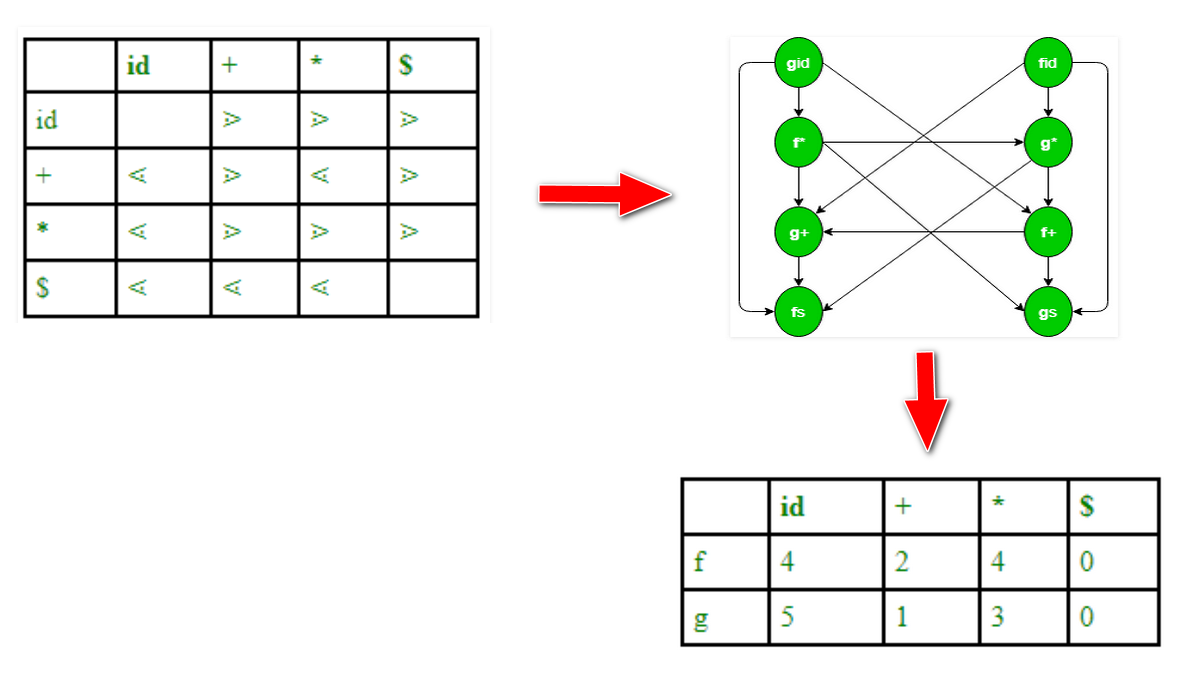
# 怎么画
- 如果a 的优先级高于或等于b,则从 $f_a$ 至 $g_b$ 画一条有向边
- 如果a 的优先级低于或等于b,则从 $g_b$ 至 $f_a$ 画一条有向边
- 注意相等的话要画来回两条边
- 每个结点赋予一个数, 该数等于从该结点出发可达结点(包括出发结点本身在内)的个数.
- 因为可能有的表没有优先函数, 所以还要检查是否有矛盾: 是否有矛盾的优先级, 即: 是否有环?
- An Illustration:
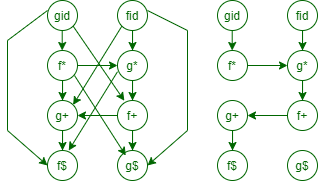 5
5
可以证明: 若$a≐b$, 则$f(a)=g(b)$; 若$a⋖ b$, 则$f(a)<g(b)$; 若$a⋗b$, 则$f(a)>g(b)$
课件上完全没有讲出错处理
https://moyangsensei.github.io/2019/05/20/%E7%BC%96%E8%AF%91%E5%8E%9F%E7%90%86%EF%BC%9A%E7%AE%97%E7%AC%A6%E4%BC%98%E5%85%88%E5%88%86%E6%9E%90/ ↩︎
https://www.cs.oberlin.edu/~bob/cs331/Class%20Notes/February/February%2017/Precedence%20Grammars.pdf ↩︎
不要混淆了"算术基本定理"与"代数基本定理"哦 ↩︎
我觉得, 这是一个很奇怪的称呼, 完全没有必要又造一个专有名词出来 ↩︎
https://www.geeksforgeeks.org/role-of-operator-precedence-parser/ ↩︎