Compiler-4-2_LR(0)_Parse
# LR (0) Parse
- 在分析 LR (0) 语法时, 我们只需要观察栈顶的元素, 根据栈顶元素来决定如何移进/归约. 这也是 LR (0) 里面"0"的含义 - 0 look ahead.
# LR (0) 项目 - LR (0) Item
LR 分析表的构造以"LR Item"为基础, “LR Item"可以理解为"在寻找句柄的过程中的一种推断”.
一个 LR (0) 项目由两部分组成: 一个产生式和一个指示栈顶位置的句点: $$E\rightarrow \alpha\cdot \beta$$
- 比如: $E\rightarrow \alpha\cdot \beta$ 代表: 我们已经识别到了 $\alpha$ ($\alpha$ 已经在栈里面了), 如果后面接下来的部分是 $\beta$, 那么就可以确定是句柄 $E\rightarrow \alpha\beta$ 了
- 即, 每一个项都代表着"句柄的一种可能性"
通常, 在一个项目集合里面有很多不同的项目:
- 比如: 下图高亮部分是一个项目集合
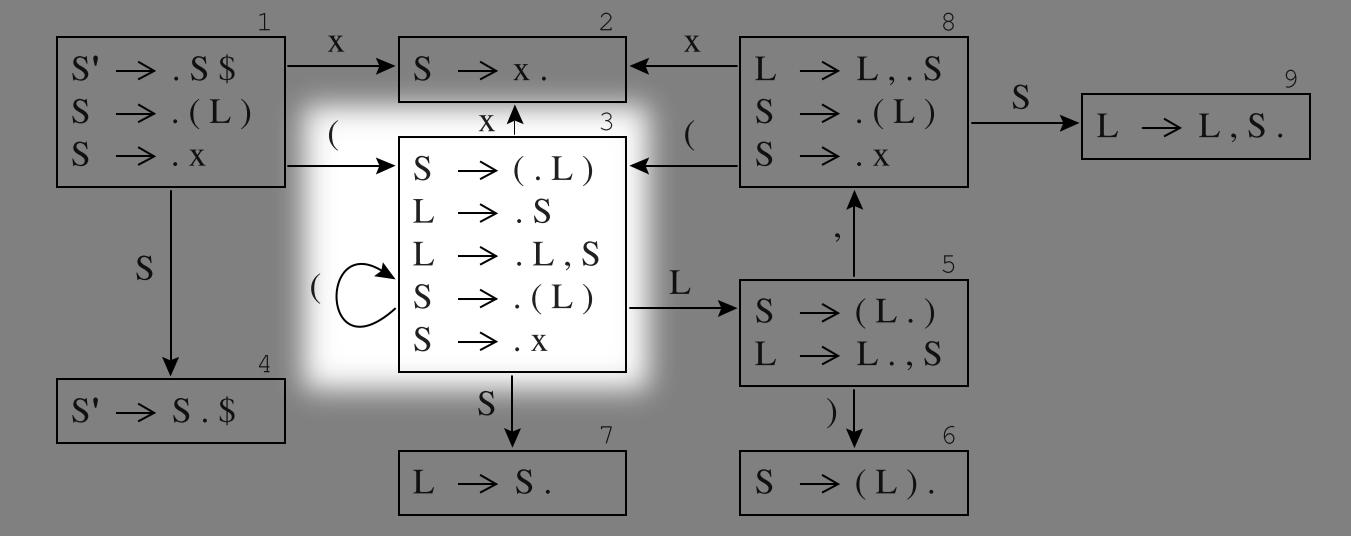
- 同一个集合里的项目看起来很不同, 但是他们"抽象的共同点"让我们将其聚合为 DFA 里面的一个等价类, 后面我们将叙述怎样寻找这种"共同点".
- Intuitively, 一个状态里面有许多不同的项的意思是: 基于现在栈里面的情况, 这些句柄是可能出现的.
- 比如: 下图高亮部分是一个项目集合
# 构建转化规则: DFA
这涉及到两个操作
- $\mathrm{Closure(一个项目集合)}\space \Rightarrow$ 求闭包, 即求出一个封闭的 LR 项目集合, 十分类似于将 NFA 转化为 DFA 里面的 $\varepsilon-$ 闭包
- $\mathrm{Goto(一个项目集合, 某个符号)}\space \Rightarrow$ 看看当前状态输入 (吃掉) 某个符号后, 会转移到哪个状态
这里可以联系形式语言与自动机的知识: 构成 DFA 有两种不同的思路: 我们可以先根据产生式构造一个 LR 项的 NFA, 然后再转化为 DFA1; 或者我们也可以直接构造 DFA. 不过 LR 分析的时候我们通常都采用后一种方法: 即从初始状态出发, 不断地根据所有可能的输入求闭包, 生成新的状态集, 直到状态数不变.
下面我们详细解释这两种操作:
# Closure (a set of items)
这是算法:

直观的来说, 这通常会让这个项 $$\mathrm{S} \rightarrow . \mathrm{L} \alpha$$ 变成这个集合: $$\begin{aligned} &\mathrm{S} \rightarrow . \mathrm{L} \alpha \\ &\mathrm{L} \rightarrow .(\mathrm{L}) \\ &\mathrm{L} \rightarrow . \mathrm{\beta} \end{aligned}$$ 可是, 为什么下面这两个新加进来的项会和上面的项拥有相同的地位呢?
我们从闭包的角度来考虑这个问题:2
- 对于这样一个转换, 可能有两种情况:
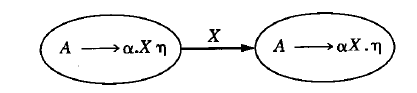
- 如果 X 是一个终结符, 那么这个转移表示将这个终结符压入栈顶, 句点前移.
- 如果 X 是一个非终结符, 情况则变得复杂起来, 因为我们分析的句子肯定是一个终结符串, 不会出现非终结符.
进一步考虑, 如果出现了非终结符 X 入栈, 那么代表着前面一定出现了对于产生式 $X\rightarrow \beta$ 的归约, 这个归约将终结符串 $\beta$ 换成了非终结符 $X$. 要出现这样的归约, 需要首先识别出可以产生 X 的句柄 $\beta$. 我们将这种思想表示为下图:
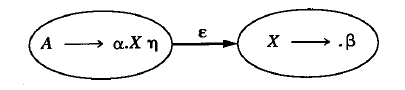 求 $\mathrm{\varepsilon-CLOSURE}$ 的时候就将两个项合并到同一个状态里面去了
求 $\mathrm{\varepsilon-CLOSURE}$ 的时候就将两个项合并到同一个状态里面去了
所以我们上面的例子可以这样理解:
# Goto (a set, a character)
这是算法:
 即对于每一个 LR 项目, 尝试向后移动一个符号 (包括终结符和非终结符), 然后再取这个转移的闭包.
即对于每一个 LR 项目, 尝试向后移动一个符号 (包括终结符和非终结符), 然后再取这个转移的闭包.
# 构建 DFA
说明了两个基本操作, 接下来便是从初始状态出发, 不断"转移, 取闭包, 转移, 取闭包……“直到整个 DFA 没有变化. 这和 NFA 转 DFA 时候的思想很相似.

这时, 我们通常会得到一个类似于下图的 DFA:
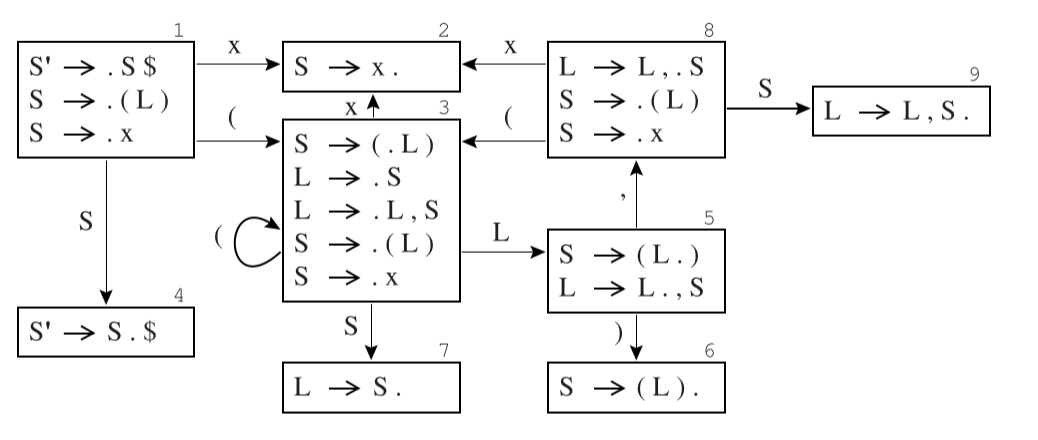
- 里面包含了 Shift 和 Goto 的所有信息, 但是还没有说明需要 Reduce 的时候该怎么办 (构造转移表的时候会解决这个问题).
在分析的时候, 使用 DFA 比使用转移表直观多了.
# 构建转移表 DFA → ACTION & GOTO tables
- 对于 DFA 里面的每一条边:
- 如果这个转移是终结符, 那么在 ACTION 表里面填上 “Shift <目标状态>”
- 如果这个转移是非终结符, 那么在 GOTO 表里面填上 “Goto <目标状态>”
- 对于包含形如 $A \rightarrow \gamma\space \textbf.$ 的状态 (即这个状态包含一个 LR 项, 这个 LR 项成功识别了一个句柄), 在 ACTION 表对应位置写上 “Reduce <产生式序号>”
- 对于包含 S′ → S.$ 项的状态, 我们在 ACTION 表填入 “Accept”, 表示分析成功. (成功识别了第一个产生式, 即产生初始符号的产生式: S′ → S.$ )
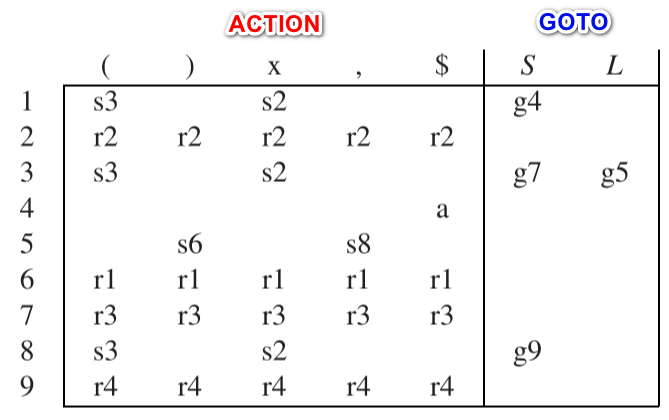
# Start Parsing
- 我们先向符号栈里面推入符号$, 表示句子的末尾, 向状态栈里面推入状态 0, 表示初始状态.
- 然后我们开始逐个读入符号, 根据表 (DFA) 来进行Shift
- 对于Reduce, 我们需要 pop 符号栈里面的句柄和状态栈里面对应的状态, (在 DFA 里面回退到句柄之前的状态), 然后再压入产生式右侧的非终结符, 进行Goto操作.
- 一直在状态之间转移, 直到
- 遇到 Accept → 分析成功,
- 或者, 遇到表中为空的项 (DFA 里面不存在的边) → 存在语法错误
相比维护符号栈和状态栈两个栈, 我们也可以只维护一个栈, 将状态和对应的符号都压到这个栈里面, 只是需要注意这样 reduce 的时候需要 pop 两倍于 RHS (产生式右侧) 长度的元素.
- 以上便是 LR (0) 文法的分析过程.
# LR (0) 文法的不足
与此同时, LR (0) 文法也有一些不足之处:
LR (0) 文法的表现能力相对较弱, 几乎所有“真正的”文法都不是 LR ( 0 ) 的.3
所以, 很多文法里面, LR (0) 的分析表里面会出现移进-归约冲突 (Shift Reduce Conflict) 或者归约-归约冲突 (Reduce-Reduce Conflict)
# 移进-归约冲突
- LR (0) 分析表的每一行要么为 Shift 或空, 要么全部为某一个归约, 也就是: DFA 的每一个状态要是有完全识别句柄的项(Reduce)就不能有终结符指出去 (不能 Shift 出去)
要是有一个地方又有 Reduce 又有 Shift, 就是一个移进归约冲突.
# 归约-归约冲突
同理, 要是有个状态里面有两个不同的完全识别的句柄: $P\rightarrow\alpha\space \cdot$ 与 $Q\rightarrow\beta\space \cdot$ 那么就出现了归约-归约冲突.
- 注意只可能出现 Shift-Reduce Conflict, 不可能出现 Goto-Reduce Conflict.
- 这是因为:
- 假设现在是状态 a, 如果下一个读入的是非终结符 N, 那么之前一定有一个归约 $N\rightarrow \alpha$ 使得 DFA 回退到了状态 a.
- 假设现在状态 a 有一个 Goto-Reduce Conflict, 那么意味着现在栈顶一定又有一个完全识别的句柄 $\beta$, 构成一个归约 $P\rightarrow\beta$.
- 这意味着在归约 $N\rightarrow \alpha$ 之前, 栈里面的状态是: $\space \cdots\beta \alpha栈顶$.
- 但是这是不可能的, 我们构造 DFA 的方式决定了 $\beta$ 一定一出现就会被归约掉, 不可能被完整的放到栈里面去.