Compiler-4-3_SLR_parse
# SLR parse
- 在 LR (0) 里面, Reduce 完全占据了一个状态, 这造成了极大的浪费:
- 回忆 LL 分析里面的 FOLLOW 集合: FOLLOW (A) = {可以立即跟在 A 后面的所有终结符}
- 一个状态需要 Reduce 代表着出现了一个完全识别句柄的项: $P\rightarrow\alpha\space \cdot$, 但是仔细想想: 我们完全可以再向后多看一个符号, 只有在下一个符号属于 FOLLOW (P) 的时候, 我们才应该规约,
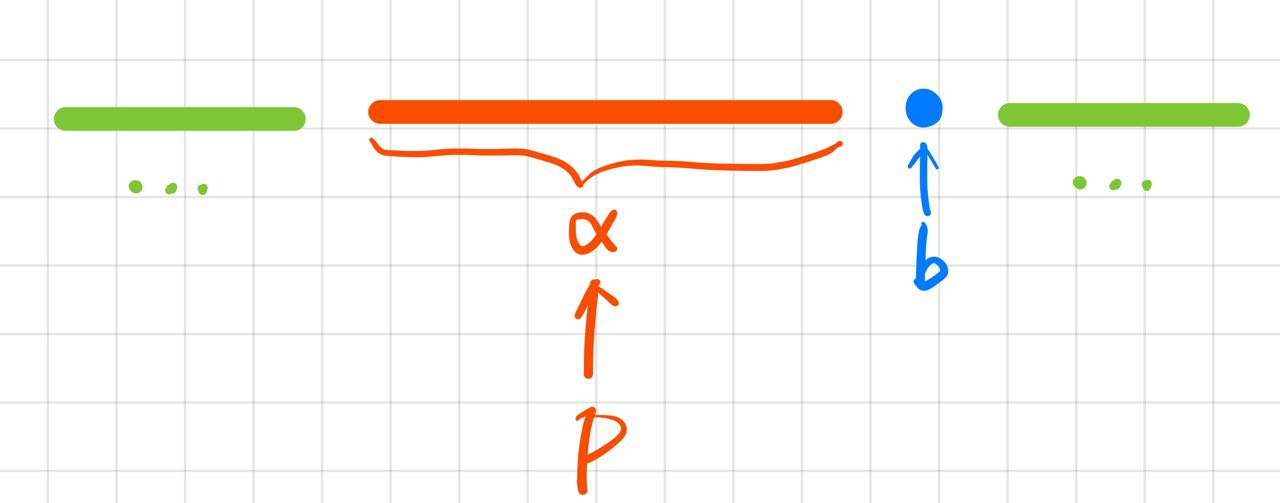
- 如上图所示, 要是 b 不在 FOLLOW (P) 里面的话, α就不应该是 $P\rightarrow\alpha$ 的句柄了, 应该继续 shift, 读进 b, 寻找句柄 $Q\rightarrow\alpha\space b\cdots$
SLR (1) 分析法就是利用 Look ahead, 看看下一个符号和规约产生式的非终结符是不是一致的, 只有在一致的时候才进行规约, 消除了部分的冲突.
# DFA 的构造
SLR (k) 分析在 DFA 的构造上和 LR (0) 分析法完全一致.
# 分析表的构造
SLR (1) 在构造分析表的时候与 LR (0) 的唯一不同就是 Reduce 的填入方式:
- LR (0) 观察每一个 set 里面的项, 只要出现完全识别句柄的项 $P\rightarrow\alpha\space \cdot$ , 就将这个状态全部标成 Reduce $P\rightarrow\alpha$
- SLR (1) 还要观察 Follow (P), 只在属于 Follow (P) 的终结符下面填入 Reduce
对比:
- 文法:
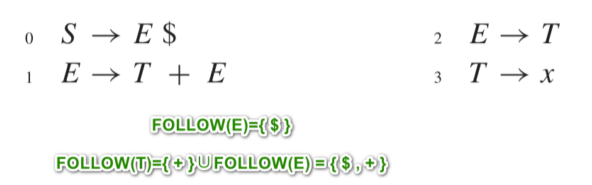
- SLR (1) 分析表:
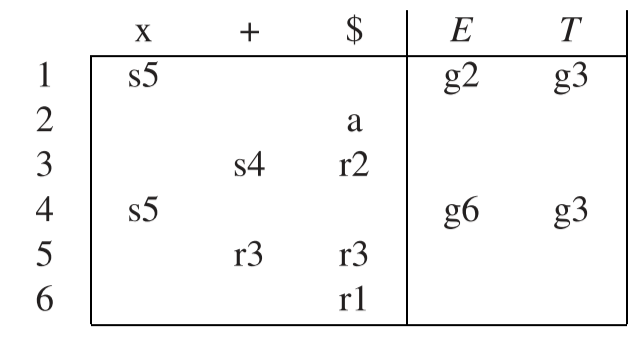
- LR (0) 分析表:
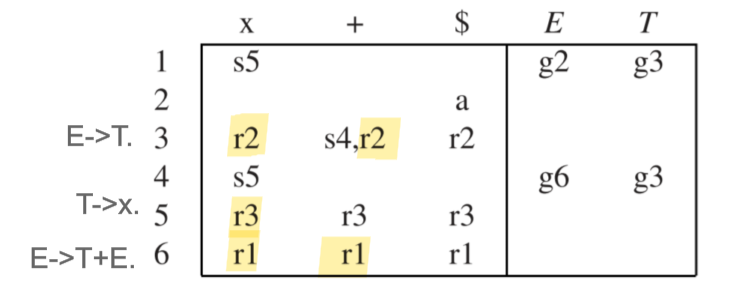
# SLR (k) - k>1
SLR (k) 顾名思义就是在填表的时候向后观察 k 个符号, 怎样观察呢?
- 除了在 Reduce 的时候观察, 还需要在 Shift 之前观察
# First Follow 集合的推广
$First(A)$ 是 A 推出的所有终结符串里面的第一个终结符 $First_k(A)$ 即 A 推出的所有终结符串里面的前 k 个终结符 (所有长度为 k 的前缀)
同理, $Follow_k(A)$ 即 A 推出的所有终结符串里面的后 k 个终结符 (所有长度为 k 的后缀)
- Shift: 对于 $A→α.Xβ$ (其中 X 是一个符号, $β$ 是产生式剩下的部分) 现在输入串是 $Xw\cdots$, 其中 $|Xw|=k$. 如果 $Xw\in First_k(Xβ)$ 那么就将 $X$ 读入, 将相应的 Shift 项填入表中. 换句话说, 如果 $Xw\in First_k(Xβ)$, 说明现在输入的前 k 个都可能被这个产生式推出, 所以我们读入 $X$.
- Reduce: 对于 $P→α.$ 现在输入串是 $w\cdots$, 其中 $w$ 是前 k 个终结符. 如果 $w\in Follow_k(P)$, 即输入串接下来的前 k 个字符可以立即跟在 P 后面, 那么将 Reduce $P→α$ 填入表中相应位置
SLR (k) 比 SLR (1) 更强大, 但是也比 SLR (1) 复杂得多. 在实际应用中, 我们通常采用后面介绍的 LALR 分析方法.
# SLR 分析方法的不足
- SLR 的不足在于: 它在分析的时候利用了 Look ahead, 但是在构建 DFA 的时候却没有考虑到 Look Head.
- 考虑下面这个 SLR (1) 的例子:
$$\begin{aligned}
&S \rightarrow \mathbf{i} \boldsymbol{d} \mid V:=E \\ &V \rightarrow \mathbf{i} \boldsymbol{d} \\ &E \rightarrow V \mid \boldsymbol{n}
\end{aligned}$$
- 其中 S 代表赋值语句 (Assign-Statement), V 代表变量 (Variable), E 代表表达式 (Expression)
- 构造状态 0: $$\begin{aligned} &S^{\prime} \rightarrow . S \\ &S \rightarrow . id \\ &S \rightarrow . V:=E \\ &V \rightarrow . id \end{aligned}$$
- 状态 0 输入终结符 $id$, shift 得到状态 1: $$\begin{aligned} &S \rightarrow id . \\ &V \rightarrow id . \end{aligned}$$
- $Follow (S)={$}, Follow (V)={$, :=}$, 所以这两个项都会在 $符号处产生一个规约, 这是一个 Reduce-Reduce 冲突.
- 但是这个冲突实际上是不存在的, 在读入 $:=$ 之前, $V \rightarrow id .$ 不应该在前瞻符号为 $ 的时候进行规约:
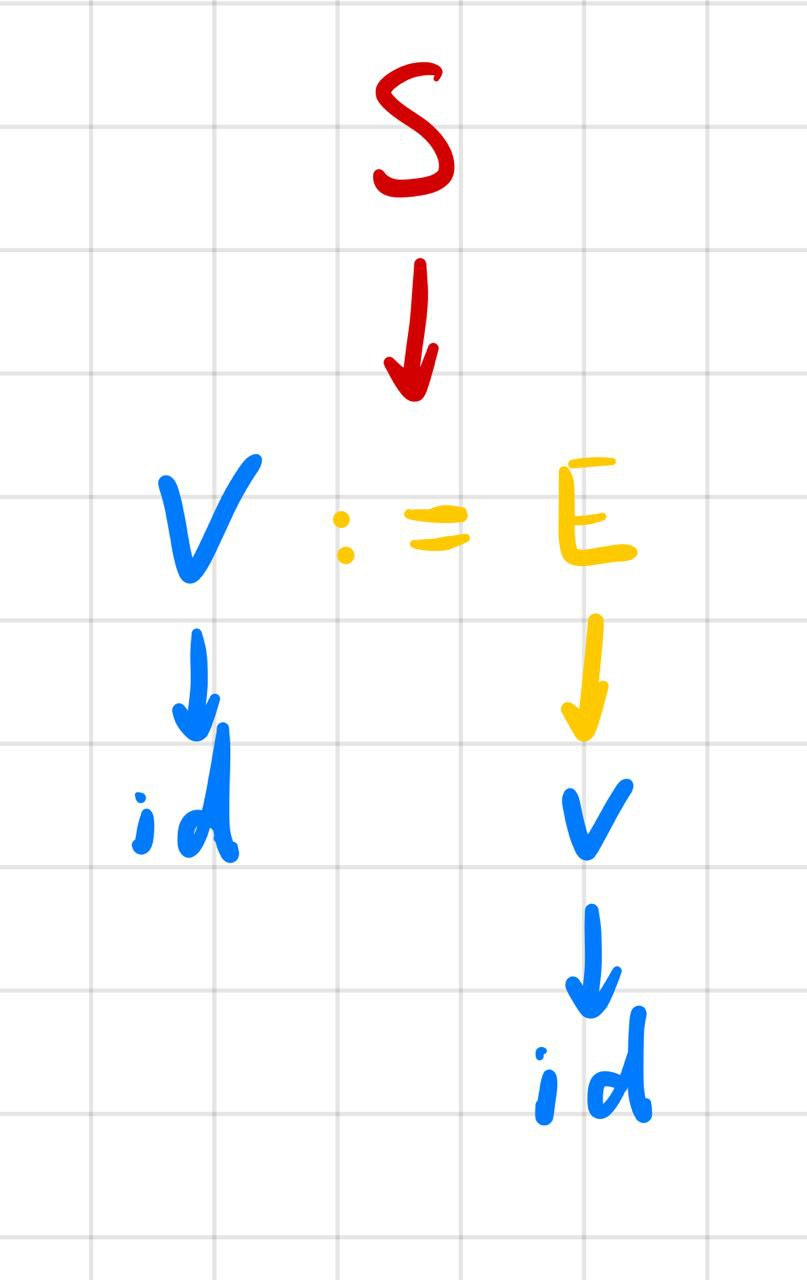
LR (1) 分析将前瞻符号的判断整合到 DFA 的构造过程中去, 解决了这个问题.