Part.29_Fisher_Linear_Discriminant(Pattern_Classification-Chapter_4)

Last updated Oct 28, 2021 Edit Source

• All
• Machine learning
• Pattern classification
• Course
• Dimensionality reduction

Tags: #MachineLearning #PatternClassification #Course #DimensionalityReduction

• 通过降维进行分类, 降到一维即为线性判别.
• 其实, 线性判别分析 (LDA)就是对Fisher线性判别的归纳.¹

• Curse of Dimensionality - 模型的表现随着维度的增加而变坏, 而且根据设计者的3维直觉, 无法很好的解决高维度的问题.
• 所以一个很直观的方法便是减少问题的维度, Fisher的方法便是将多维样本直接映射到一维的一种方法.
• 直接映射到一维是否太粗暴? 2维, 3维可以吗?
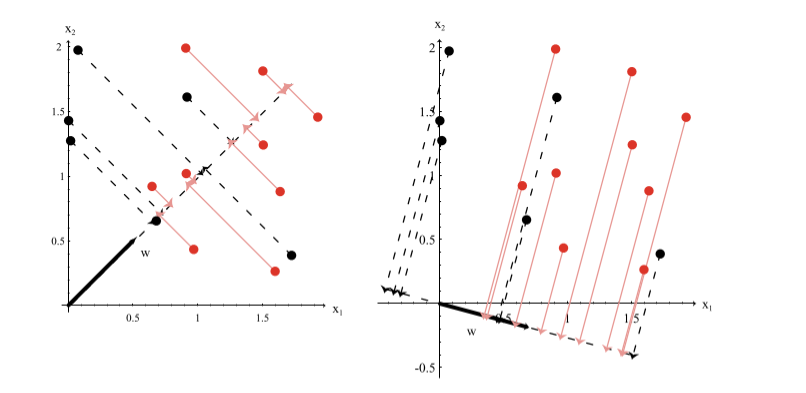
  • 的确, even if the samples formed well-separated, compact clusters in d-space, projection onto an arbitrary line will usually produce a confused mixture of samples from all of the classes, and thus poor recognition performance. However, 一维的问题是十分简单的, by moving the line around, we might be able to find an orientation for which the projected samples are well separated. This is exactly the goal of classical discriminant analysis. 二维, 三维也是可以的, 我们后面会谈到对于Fisher方法的多维推广.

Dot_Product_and_Linear_Transformation-向量内积与线性变换

协方差矩阵_Covariance_Matrix

https://sthalles.github.io/fisher-linear-discriminant/

如果我们直接投影到样本均值的连线的方向的话, 可以看到将会有很多的重合:

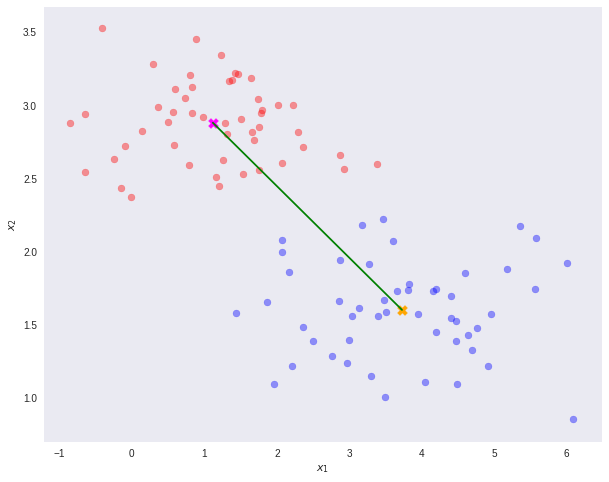
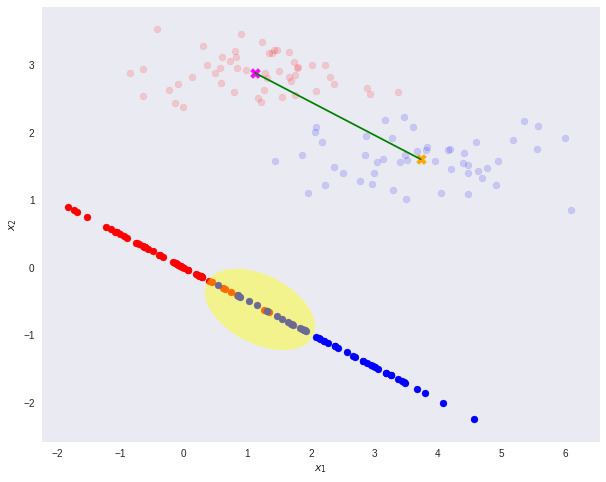
Fisher的方法基于以下直觉:

• 我们要使投影后的结果:
  1. 不同类间隔得越开越好 (类间方差最大)
  2. 相同类内聚集的越紧密越好 (类内方差最小)

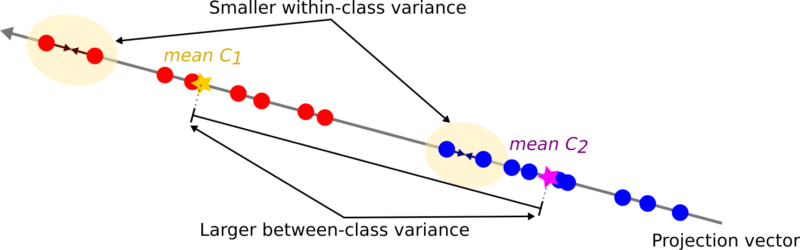所以我们这样构造准则函数(Criterion Function):

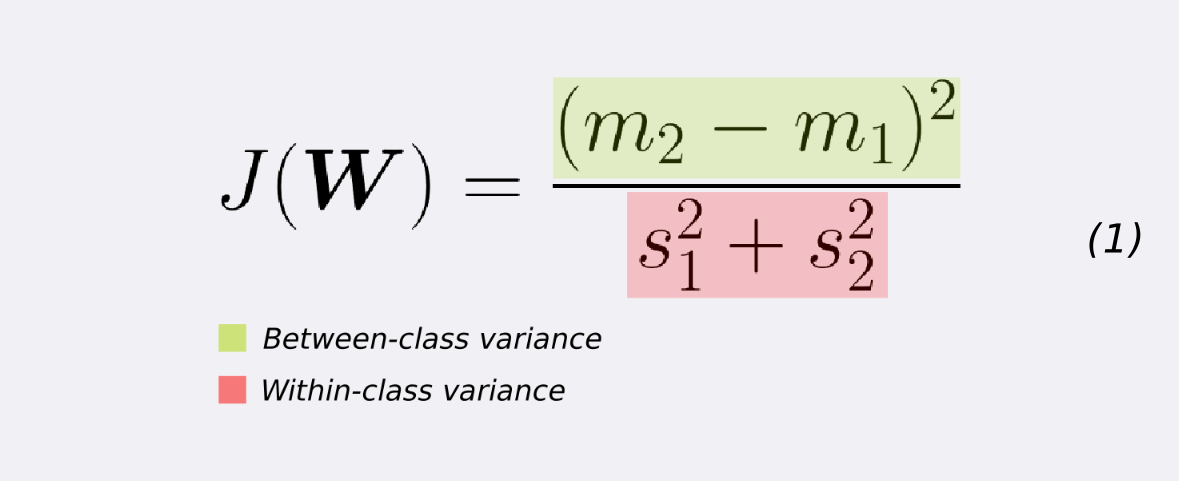我们需要找到使$J(w)$取得最大值的$w$, 即找到最优的投影方向.

• 我们这样计算投影: $$y=\mathbf{w}^{t} \mathbf{x_p}$$ 上面的式子将样本点$\mathbf{x_p}$投影到$\mathbf{w}$方向的一条直线上

• 我们这样表示类别$i$样本的均值: $$\mathbf{m}{i}=\frac{1}{n{i}} \sum_{\mathbf{x} \in \mathcal{D}_{i}} \mathbf{x}$$ 其中$n_i$是该类别样本的个数

• 我们这样计算投影后的样本均值: $$\begin{align} \tilde{m}{i}&=\frac{1}{n{i}} \sum_{y \in \mathcal{Y}{i}} y \\ &=\frac{1}{n{i}} \sum_{\mathbf{x} \in \mathcal{D}{i}} \mathbf{w}^{t} \mathbf{x}\\ &=\mathbf{w}^{t} \mathbf{m}{i}\end{align}$$ 可以发现, 投影后的均值 其实就是 均值$\mathbf{m}_{i}$的投影

• 所以我们可以这样衡量投影后的直线上面不同类间均值的距离: $$\left|\tilde{m}{1}-\tilde{m}{2}\right| =\left|\mathbf{w}^{t}\left(\mathbf{m}{1}-\mathbf{m}{2}\right)\right|$$

• 为了衡量投影后样本的分散程度, 我们定义 “类内散度” $$\tilde{s}{i}^{2}= \sum{y \in \mathcal{Y}{i}}\left(y-\tilde{m}{i}\right)^{2}$$ 直观看来, 就是投影后样本与均值距离的平方

• 然后我们就可以根据直觉, 给出Fisher准则函数如下: $$J(\mathbf{w})= \frac{\left|\tilde{m}{1}-\tilde{m}{2}\right|^{2}}{\tilde{s}{1}^{2}+\tilde{s}{2}^{2}}$$ 分子是类间的方差(越大越好), 分母是类内的方差(越小越好)

• $J(\mathbf{w})$并不是与$\mathbf{w}$直接相关的, 所以先进如下变换:

• 我们先定义Scatter Matrix $\mathbf{S_i, S_w}$: $$\mathbf{S}{i}= \sum{\mathbf{x} \in \mathcal{D}{i}} \left(\mathbf{x}-\mathbf{m}{i}\right)\left(\mathbf{x}-\mathbf{m}{i}\right)^{t}$$ $$\mathbf{S{w}} = \mathbf{S_1+S_2}$$

• 所以, 类内散度可以变为: $$\begin{aligned} \tilde{s}{i}^{2} &=\sum{\mathbf{x} \in \mathcal{D}{i}}\left(\mathbf{w}^{t} \mathbf{x}-\mathbf{w}^{t} \mathbf{m}{i}\right)^{2} \\ &=\sum_{\mathbf{x} \in \mathcal{D}{i}} \mathbf{w}^{t}\left(\mathbf{x}-\mathbf{m}{i}\right) \left(\mathbf{w}^{t}\left(\mathbf{x}-\mathbf{m}{i}\right)\right)^T \\ &=\sum{\mathbf{x} \in \mathcal{D}{i}} \mathbf{w}^{t}\left(\mathbf{x}-\mathbf{m}{i}\right)\left(\mathbf{x}-\mathbf{m}{i}\right)^{t} \mathbf{w} \\ &=\mathbf{w}^{t} \mathbf{S}{i} \mathbf{w} \end{aligned}$$

• 然后 $$\tilde{s}{1}^{2}+\tilde{s}{2}^{2}=\mathbf{w}^{t} \mathbf{S}_{W} \mathbf{w}$$ 这样, 我们将分母里面的$\mathbf{w}$提取到了外面

• 对于分子, 我们可以有相似的操作: $$\begin{aligned} \left(\tilde{m}{1}-\tilde{m}{2}\right)^{2} &=\left(\mathbf{w}^{t} \mathbf{m}{1}-\mathbf{w}^{t} \mathbf{m}{2}\right)^{2} \\ &=\mathbf{w}^{t}\left(\mathbf{m}{1}-\mathbf{m}{2}\right)\left(\mathbf{m}{1}-\mathbf{m}{2}\right)^{t} \mathbf{w} \\ &=\mathbf{w}^{t} \mathbf{S}{B} \mathbf{w} \end{aligned}$$ 观察里面的中间部分, 我们定义: $$\mathbf{S}{B}=\left(\mathbf{m}{1}-\mathbf{m}{2}\right)\left(\mathbf{m}{1}-\mathbf{m}{2}\right)^{t}$$

• 所以Criterion Function 变为了: $$J(\mathbf{w})=\frac{\mathbf{w}^{t} \mathbf{S}{B} \mathbf{w}}{\mathbf{w}^{t} \mathbf{S}{W} \mathbf{w}}$$

  这一表达式在数学物理中被称作广义Rayleigh 商(generalized Rayleigh quotient)

We call $S_{W}$ the within-class scatter matrix. It is proportional to the sample covariance matrix for the pooled $d$-dimensional data. It is symmetric and positive semi-definite, and is usually non-singular if $n>d$. Likewise, $\mathbf{S}{B}$ is called the between class scatter matrix. It is also symmetric and positive semi-definite, but because it is the outer product of two vectors, its rank is at most one. In particular, for any $\mathrm{w}$, $\mathbf{S}{B} \mathbf{w}$ is in the direction of $\mathbf{m}{1}-\mathbf{m}{2}$, and $\mathbf{S}_{B}$ is quite singular.

解$\mathbf{w}$需要用到拉格朗日乘子法: 思路: 用拉格朗日乘子法得到以下条件 $$\mathbf{S}{B} \mathbf{w}=\lambda \mathbf{S}{W} \mathbf{w}$$ If $\mathbf{S}{W}$ is non-singular we can obtain a conventional eigenvalue problem by writing $$\mathbf{S}{W}^{-1} \mathbf{S}{B} \mathbf{w}=\lambda \mathbf{w}$$ In our particular case, it is unnecessary to solve for the eigenvalues and eigenvectors of $\mathbf{S}{W}^{-1} \mathbf{S}_{B}$ due to the fact that $\mathbf{S_B w}$ is always in the direction of $m_1 −m_2$. Since the scale factor for $\mathbf{w}$ is immaterial, we can immediately write the solution for the $\mathbf{w}$ that optimizes $J(·)$:

$$\mathbf{w}=\mathbf{S}{W}^{-1}\left(\mathbf{m}{1}-\mathbf{m}_{2}\right)$$

详细过程

• Ref 模式识别(第三版) - 张学工, Page 64

• Ref 机器学习 周志华

• Ref 南瓜书

推广到高维:² 我们需要改变以下地方:

• 
• 类内 Scatter Matrix, $S_W$直观的来说, 即从两个类的 $S_1+S_2$ 变成多个类 $S_i$ 的和
• 对于$S_B$, 变成了 “每个类相对于全局平均的差” 的加权和, 这里和只有两个类的情况并不是完全一致的, 具体参见 Duda 模式分类, page49

若将 W 视为一个投影矩阵，则多分类 LDA 将样本投影到 N-1 维空间，N-1 通常远小子数据原有的属性数. 于是，可通过这个投影来减小样本点的维数，且投影过程中使用了类别信息, 因此 LDA 也常被视为一种经典的监督降维技术³