理解相似矩阵

Last updated Nov 14, 2021 Edit Source

• All
• Math linear algebra

Tags: #Math/LinearAlgebra

• 设 $A,B$ 都是 $n$ 阶矩阵，若有可逆矩阵 $P$ , 使得 $B=P^{-1}AP$ , 则称$B$是$A$的相似矩阵。

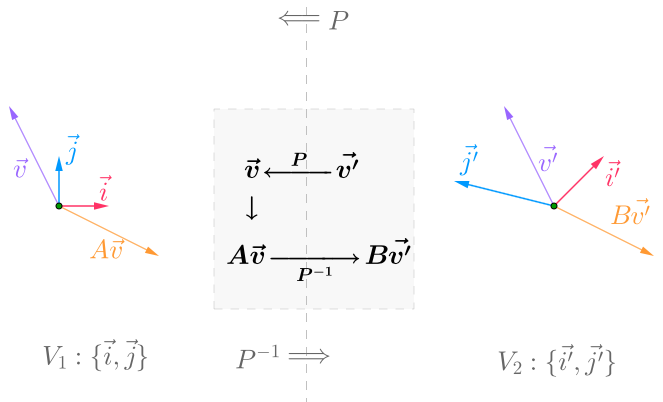
• 相似矩阵是同一个线性变换在不同基向量下的不同矩阵表示.

  • $P$是基变换矩阵(Base Change Matrix), 它是一个不改变空间维数的可逆线性变换, 其目的是改变当前线性空间的基底: $(\space \vec i’,\space \vec j’\space )\rightarrow (\space \vec i,\space \vec j\space )$, 也可以理解为进行坐标换算, 但是不改变空间里面的实际位置

所以图里面右边的 $$v’\rightarrow Bv’$$ 等价于

• 先变换基底到$V_1$, 得到位置相同但是坐标不同的向量$v$ $$v’\rightarrow Pv’$$
• 然后进行$V_1$下面等价的线性变换$A$, 得到$V_1$下的结果$Av$ $$v’\rightarrow Pv’\rightarrow APv’$$
• 最后再把基底换回来, 得到$V_2$里面的结果 $$v’\rightarrow Pv’\rightarrow APv’\rightarrow P^{-1}APv’$$

我们有: $$P^{-1}AP = B$$

¹