MIT_18.065-Part_1-A_Column_Space_Perspective
# The Column Space of A Contains All Vectors Ax
Tags: #Math/LinearAlgebra
Video Link: 1. The Column Space of A Contains All Vectors Ax - YouTube
- This video reviewed some of the basic ideas of Linear algebra, especially “the right way to think of a matrix”.
# 理解Ax - 列空间
$$Ax$$
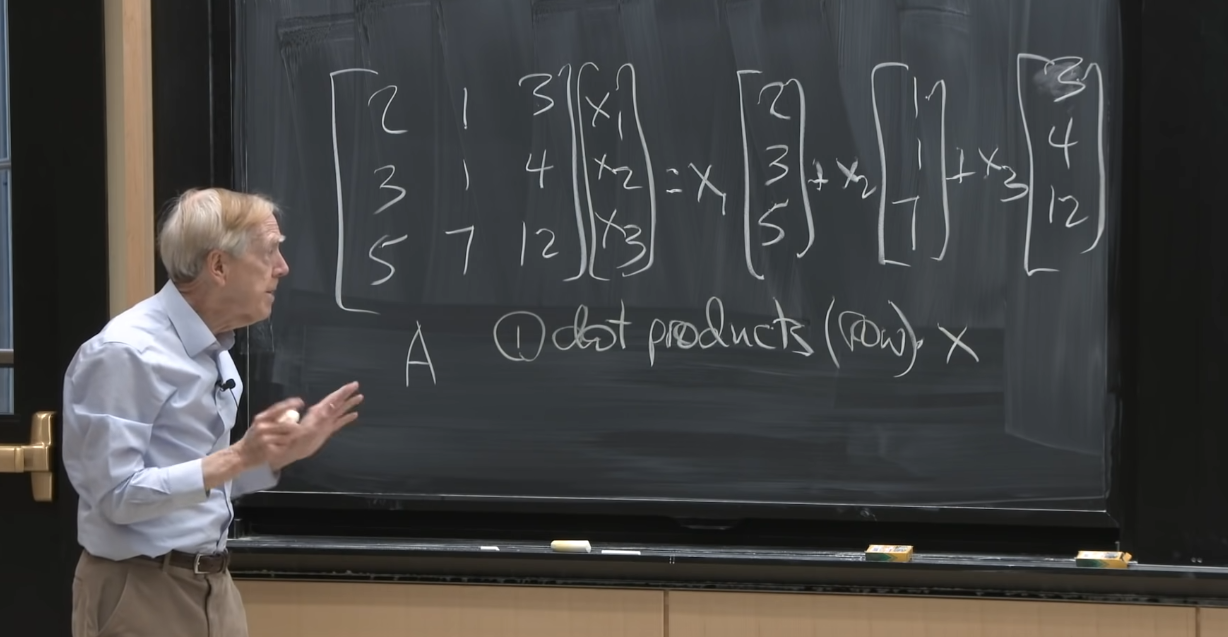看待矩阵与向量乘积的两种方式:
- A的行向量与x的dot product - Not Intuitive
- A的列向量的线性组合 - Intuitive
进一步, Ax可以表示Col(A), 即A的列空间.
- Rank(A)就是A里面独立的列向量个数
这可以带来一种有趣的分解形式:
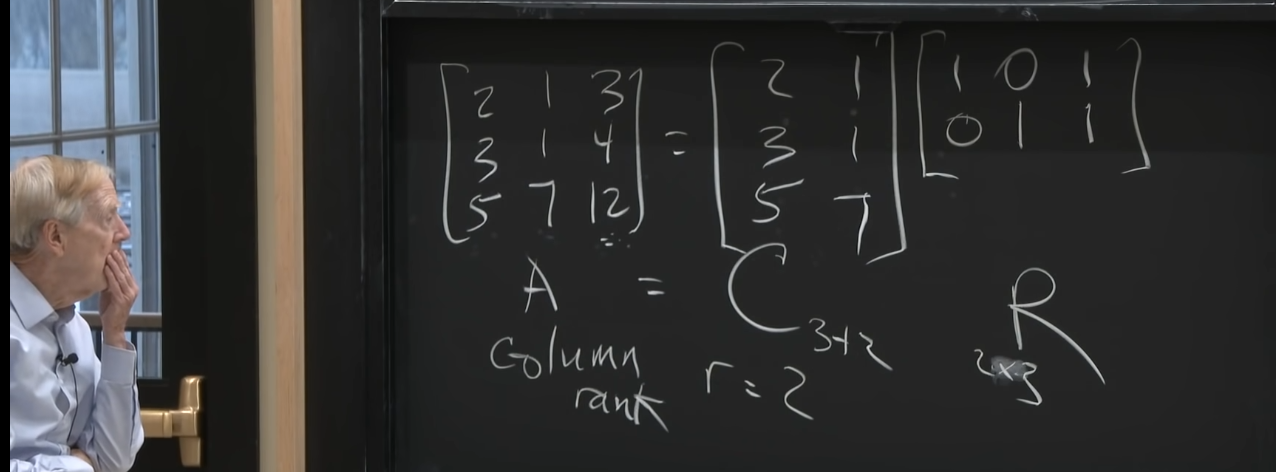
$$A=CR$$
$$A_{3\times 3}=C_{3\times 2}R_{2\times 3}$$
在矩阵C里面列都是独立的, 且构成Col(A)的基向量, 在矩阵R里面行也都是独立的, 也构成Row(A)的基向量. 这解释了一个重要的事实:
- 矩阵的行秩等于列秩
The big factorization for data science is the “SVD” of A-when the first factor C has r orthogonal columns and the second factor R has r orthogonal rows.
Actually R is a famous matrix in linear algebra: R = rref(A) = row-reduced echelon form of A (without zero rows). (A的行化简最简阶梯型)1
$A=CR$的一个更一般的形式:
# 理解AB
$$A_{m\times n}B_{n\times p}= M_{m\times p}$$
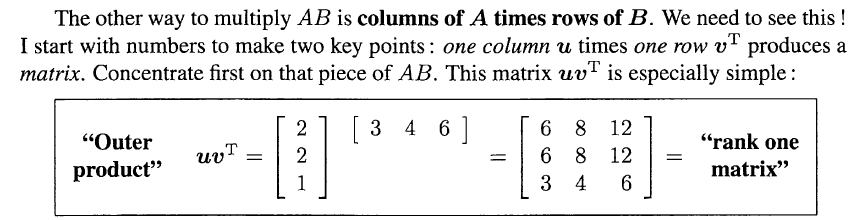
我们用A的列向量乘上B的行向量, 得到一个矩阵, 这个矩阵构成了"the perfect building blocks for every matrix."
两个矩阵的积就是n个这样矩阵的加和.
每一个矩阵的方向都是A里面一个列向量的方向, 即上面u的方向
每一个矩阵的秩都为1, 所以AB即n个秩为一的矩阵的加和:
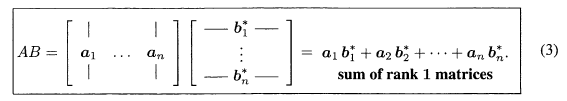
对比一下我们原来的思考方式, 两种方法分别对应向量的内积与外积:
