MIT_18.065-Part_11-SVD_&_Linear_System
# SVD & Linear System
Tags: #LinearRegression #SVD #Math/LinearAlgebra
# $Ax=b$
对于这个线性约束方程组: $$Ax=b$$
只有在A可逆的方阵的时候, 才有唯一解: $$x=A^{-1}b$$
而在A为其他形状的时候, 常常不能够简单的利用$A^{-1}$来求解这个方程组
- Under-determined: (不定方程)
- 这时我们没有足够的约束来限制x, x常常有无穷解
- 换一个看法, 这可以看作因为$Row(A)$没有填满$R^n$, 所以我们可以在每一个解里面加上一部分核空间里面的向量$x_{kernel}$, 同时不影响方程的成立:
- $$\begin{aligned}&A(x+x_{kernel})=b \\Rightarrow &Ax+Ax_{kernel}=b\\Rightarrow &Ax+0=b\end{aligned}$$
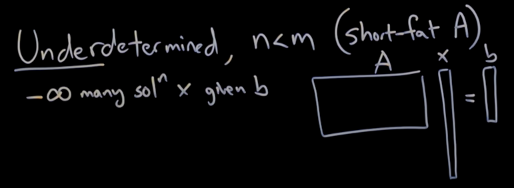
- Over-determined: (超定方程)
- 在这个情况下, 我们有太多限制来限制x, 所以有可能出现矛盾, 导致x没有解.
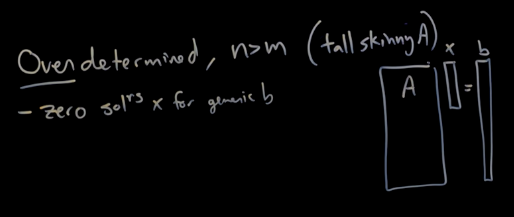
# Pseudo-Inverse & SVD
对于长方形的情况, 我们可以定义矩阵A的"伪逆"(Pseudo-Inverse): $A^+$. 这样我们可以近似地求解不理想情况下的线性方程组
我们定义$A^+$如下
- 由SVD有: $$A=U\Sigma V^T$$ $$\begin{aligned}&\quad \quad Ax=b \\ &\Rightarrow\quad U\Sigma V^Tx=b\\ &\Rightarrow\quad x=V\Sigma^{-1}U^Tb\end{aligned}$$
- $$A^+=V\Sigma^{-1}U^T$$
这样, 我们就通过SVD得到了广义逆
在$A$是可逆方阵的时候, 广义逆等于$A^{-1}$ : $$A^{-1}=(U\Sigma V^T)^{-1}={(V^T)}^{-1}\Sigma^{-1}U^{-1}=V\Sigma^{-1}U^T$$
- 这个广义逆也称为 Moore–Penrose inverse
# Using Pseudo-Inverse to Solve $Ax=b$
$$x=A^+b$$ $$x=V\Sigma^{-1}U^Tb$$
在不定方程的情况下, 这个解是无穷多个解里面$l_2$ norm最小的

在超定方程的情况下, 这个解是最小二乘解, 即Least Square解, 是b向量对A的列空间上面的投影.
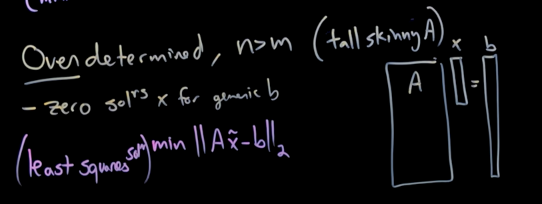
我们得到的近似解$\hat x$到底是什么呢? 我们可以再计算$A\hat x$ : $$\begin{aligned}A\hat x&=AA^+b\\ &=(U\Sigma V^T)(V\Sigma^{-1}U^T)b\\ &=UU^Tb\end{aligned}$$
注意: 如果我们的U是Economy SVD里面的$\hat U$, 即只取有效的前r列的U, 那么$UU^T\neq I$.
Source: Linear Systems of Equations, Least Squares Regression, Pseudoinverse - YouTube