MIT_18.065-Part_2-Matrix_Factorization
# 矩阵分解
2021-11-12
Tags: #Matrix #Math/LinearAlgebra #Math

- 我们看待矩阵乘积的新方式有助于我们理解数据科学里面对矩阵的各种分解. 我们常常需要发掘一个矩阵$A$里面隐藏的信息, 而通过将$A$分解为$CR$, 我们可以观察A里面最基本的组成部分: 秩为1的矩阵: $col_k(C)\space row_k(R)$

下面列举重要的分解, 在详细论述后将补充相应细节
# 五个重要的矩阵分解
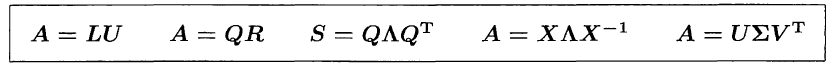
# $LU$分解 : $A=L U$
- $A=L U$ 可以理解为矩阵的化简(elimination).
- $L$ 代表 Lower Triangular, 是一个下三角矩阵, 同理, $U$代表Upper Triangular, 是一个上三角矩阵.
- LU分解可以被视为高斯消去法的矩阵形式。$L$ 是高斯消元法的过程, 而$U$是高斯消元法的结果. 看下面这个例子:
- LU分解的例子
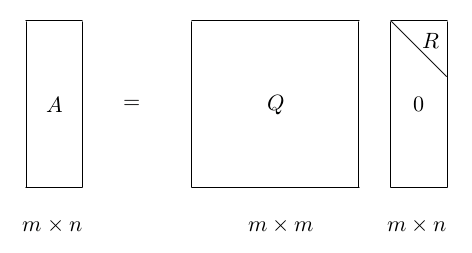
# 正交分解 : $A=Q R$
通过将矩阵 $A$ 的列$\boldsymbol{a}{1}$ 到 $\boldsymbol{a}{n}$“正交化” (orthogonalize), 我们就得到了正交分解$A=Q R$
其中:
- 矩阵 $Q$ 的列相互正交 (orthonormal), 如果列向量长度为一, 还有: $Q^{\mathrm{T}} Q=I$ ,
- $R$ 是一个上三角矩阵(可能不是方阵).
正交化常用的方法是 “Gram-Schmidt” 方法.
# $S=Q \Lambda Q^{\mathrm{T}}$
$S=Q \Lambda Q^{\mathrm{T}}$ comes from the eigenvalues $\lambda_{1}, \ldots, \lambda_{n}$ of a symmetric matrix $S=S^{\mathrm{T}}$ Eigenvalues on the diagonal of $\Lambda$. Orthonormal eigenvectors in the columns of $Q$.
S是对称矩阵, Q是S的正交特征列向量, $\Lambda$是特征值组成的对角矩阵.
MIT_18.065-Part_3-A_Different_Perspectvie_of_Matrix_Multiplication-An_Example
# $A=X \Lambda X^{-1}$
- $A=X \Lambda X^{-1}$ is diagonalization when $A$ is $n$ by $n$ with $n$ independent eigenvectors. Eigenvalues of $A$ on the diagonal of $\Lambda$. Eigenvectors of $A$ in the columns of $X$.
# $A=U \Sigma V^{\mathrm{T}}$
- $A=U \Sigma V^{\mathrm{T}}$ is the Singular Value Decomposition of any matrix $A$ (square or not). Singular values $\sigma_{1}, \ldots, \sigma_{r}$ in $\Sigma$. Orthonormal singular vectors in $U$ and $V$.