MIT_18.065-Part_4-LU_Factorization
# LU 分解
Tags: #Math/LinearAlgebra #Math #Matrix
$A=L U$
Key Idea: 怎样从A = Sum of Rank 1 Matrices的角度来理解这个分解?
简单的概念回顾:
# 看待Ax=B的两个角度
# Row Perspective
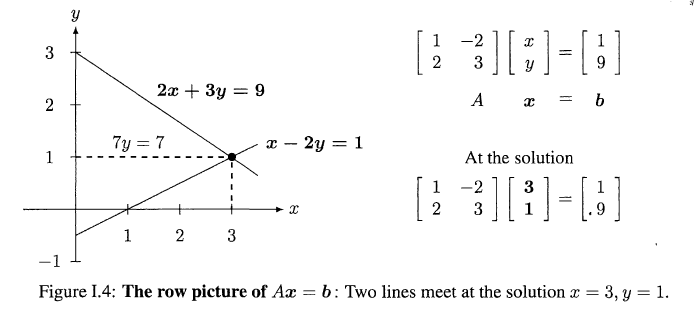
- 几个约束方程的公共解, 即超平面在空间里面共同的交点
# Column Perspective
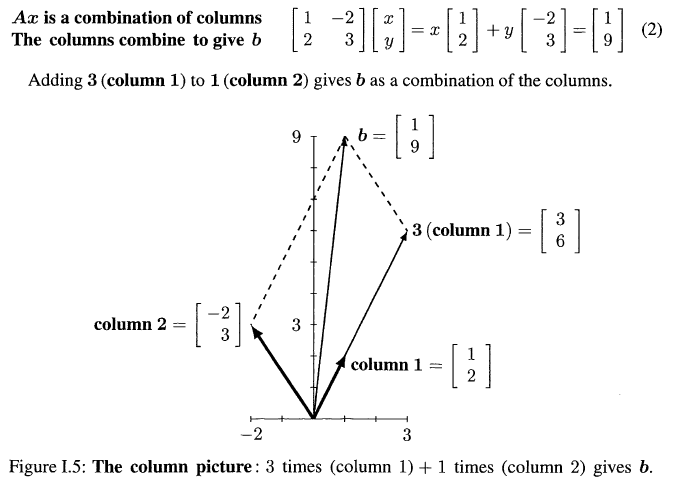
利用基向量来表达目标向量
对于二维的问题Row Perspective 看起来还行, 但是对于多维的情形, Column Perspective更加直观(想象好几个超平面的交点是很困难的!)
# 回顾A=LU的分解步骤
- 从上面的例子里面我们能够得到一种直觉: 求LU分解的过程就是每次解决一列, 直到结果完全变成三角矩阵.
- Intuition:
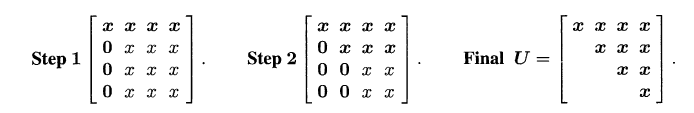
# The “Sum of Rank 1 Matrices” Perspective
- How is the original A related to the final matrix U ?
$$\boldsymbol{A}=\boldsymbol{\ell}{\mathbf{1}} \boldsymbol{u}{\mathbf{1}}^{}+\boldsymbol{\ell}{\mathbf{2}} \boldsymbol{u}{\mathbf{2}}^{}+\boldsymbol{\ell}{\mathbf{3}} \boldsymbol{u}{\mathbf{3}}^{}+\boldsymbol{\ell}{\mathbf{4}} \boldsymbol{u}{\mathbf{4}}^{}=\left[\begin{array}{cccc} 1 & 0 & 0 & 0 \\ \ell_{21} & 1 & 0 & 0 \\ \ell_{31} & \ell_{32} & 1 & 0 \\ \ell_{41} & \ell_{42} & \ell_{43} & 1 \end{array}\right]\left[\begin{array}{l} \text { pivot row 1 } \\ \text { pivot row 2 } \\ \text { pivot row 3 } \\ \text { pivot row 4 } \end{array}\right]=\boldsymbol{L} \boldsymbol{U}$$
每一个Rank为1的矩阵都"处理(peel off)“它对应的一行一列, 所有的矩阵加起来就构成了A:
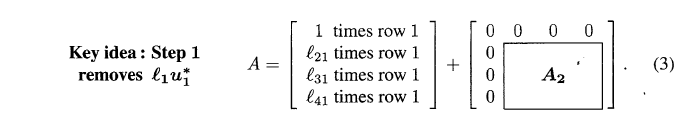
- Intuition:
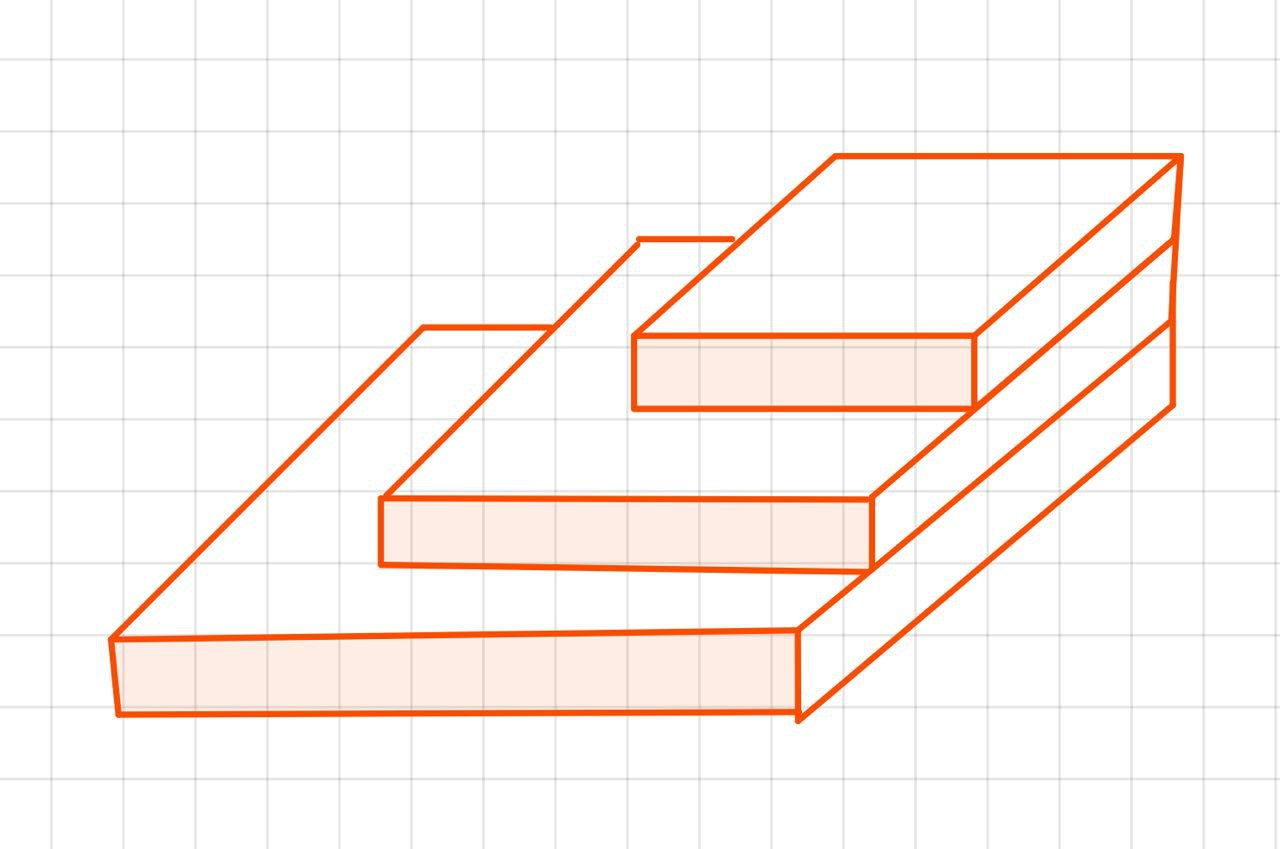方向好像画错了, 但是You Get the Idea.
# With Row Exchange
上面的分解都是不带Row Exchange的, 但是有时候Pivot是0, 我们就需要交换一下行, 用对应位置非零的行来作为Pivot:
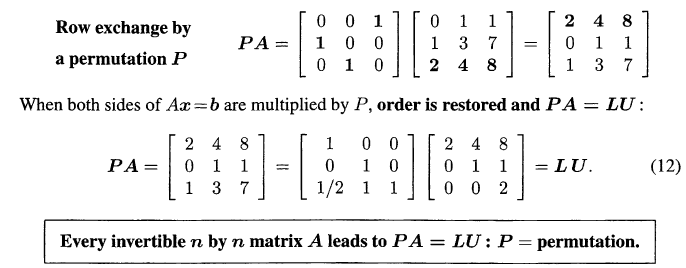
这是就变成了PLU分解, 维基百科上面有更详细的叙述