MIT_18.065-Part_5-Four_Subspaces

Last updated Nov 13, 2021 Edit Source

• All
• Math linear algebra

Tags: #Math/LinearAlgebra

The Four Subspaces are:

• $A$的列空间 $Col(A)$
• $A$的行空间 $Row(A)=Col(A^T)$
• $A$的核(零空间) $N(A) \Rightarrow Ax=0$
• $A^T$的核 $N(A^T) \Rightarrow A^Ty=0$

为了与课本一致, 我们将$Col(A)$简称为$C(A)$

怎样理解这四个子空间呢?

对于$A_{m\times n}$, 假设$Rank(A)=r$

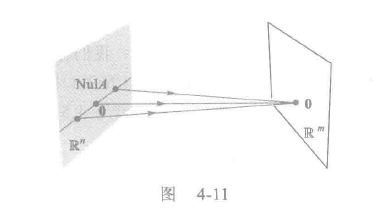
• 从线性映射的角度来看, $A_{m\times n}$是从$\mathbf{R^n}$到$\mathbf{R^m}$的一个映射

• $C(A)$是A的列空间, 即列向量张成的子空间

  • 每个列向量是m维的, 所以$C(A)$属于 $\mathbf{R^m}$
  • $dim(C(A))=r$

• $C(A^T)$是A的行空间, 即行向量张成的子空间

  • 每个行向量是n维的, 所以$C(A^T)$属于 $\mathbf{R^n}$
  • $dim(C(A))=r$

• $N(A)$是$Ax=0$的解空间, 属于映射前的空间$\mathbf{R^n}$. 与行向量在同一个维度的空间下.

  • $dim(N(A))=n-r$ ¹

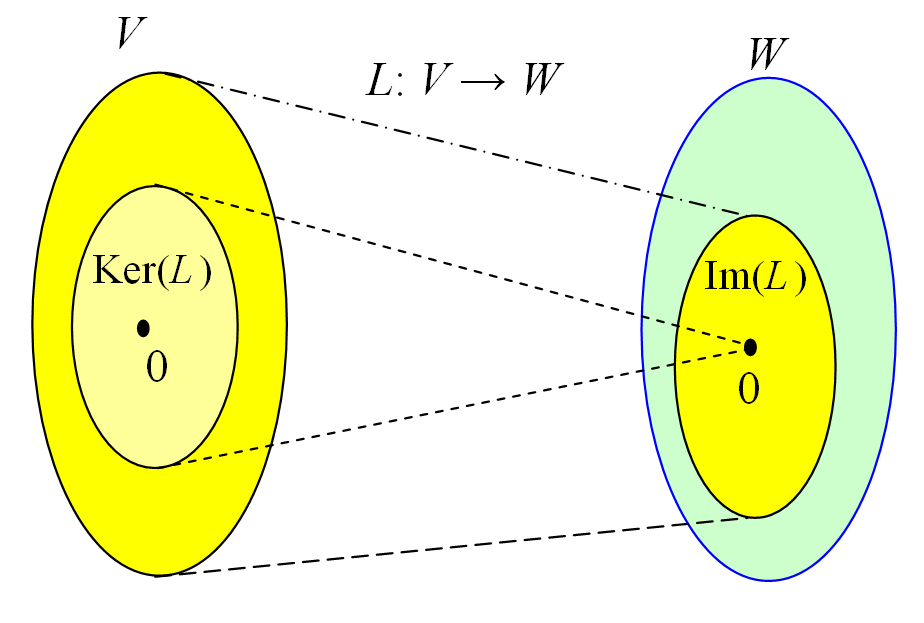
• $N(A^T)$是$A^Ty=0$的解空间, 属于映射后的空间$\mathbf{R^m}$. 与列向量在同一个维度的空间下.
  • $dim(N(A^T))=m-r$

• A great video: Visualizing the Four Fundamental Spaces - YouTube

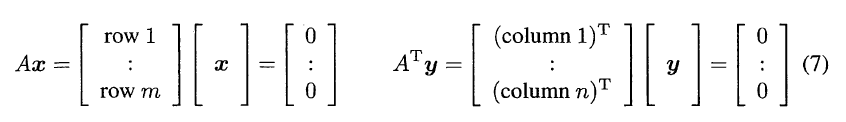
• “A的每一行与x的内积都为0”, 所以$N(A)\perp Row(A)\Rightarrow N(A)\perp C(A^T)$

• 同理, $C(A)\perp N(A^T)$

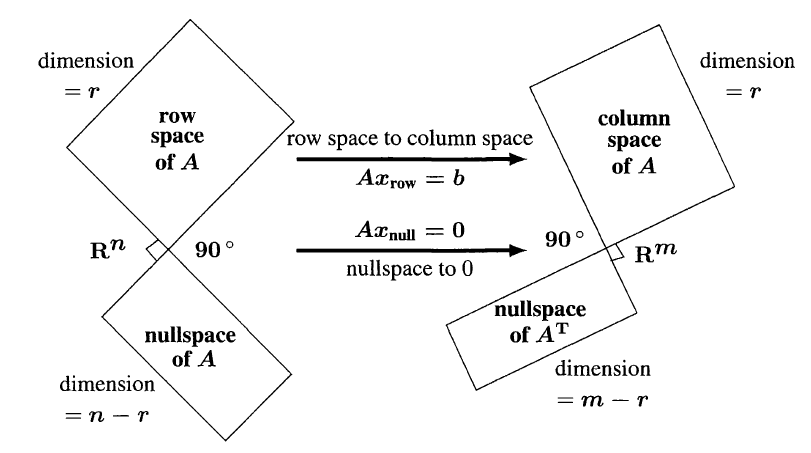
• 两个子空间在$\mathbf{R^n}$, 两个子空间在$\mathbf{R^m}$, 同一个维度的两个子空间相互垂直, 一起填满整个空间

• 不同维度的空间通过一个线性映射联系起来, $A_{m\times n}$将$\mathbf{R^n}$映射到$\mathbf{R^m}$

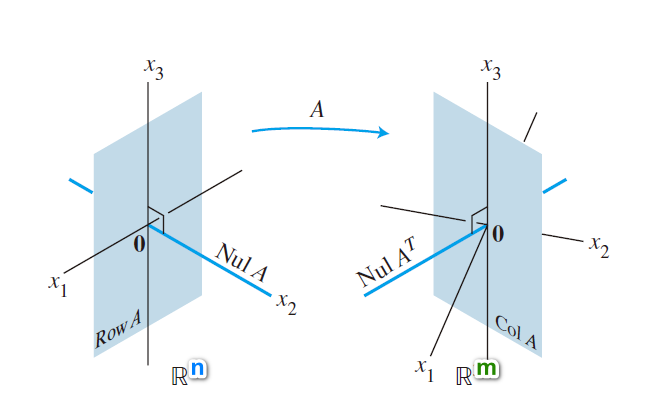
• 每一个$\mathbf{R^n}$里面的向量$\mathbf{R^n}$都有一部分在$Row(A)$里面, 有一部分在$Null(A)$里面. 映射过去以后, 便都在ColA里面了.

  • x全部在$Null(A)$里面的时候, 映射过去就是0向量
  • 映射的过程其实可以看成两部分: 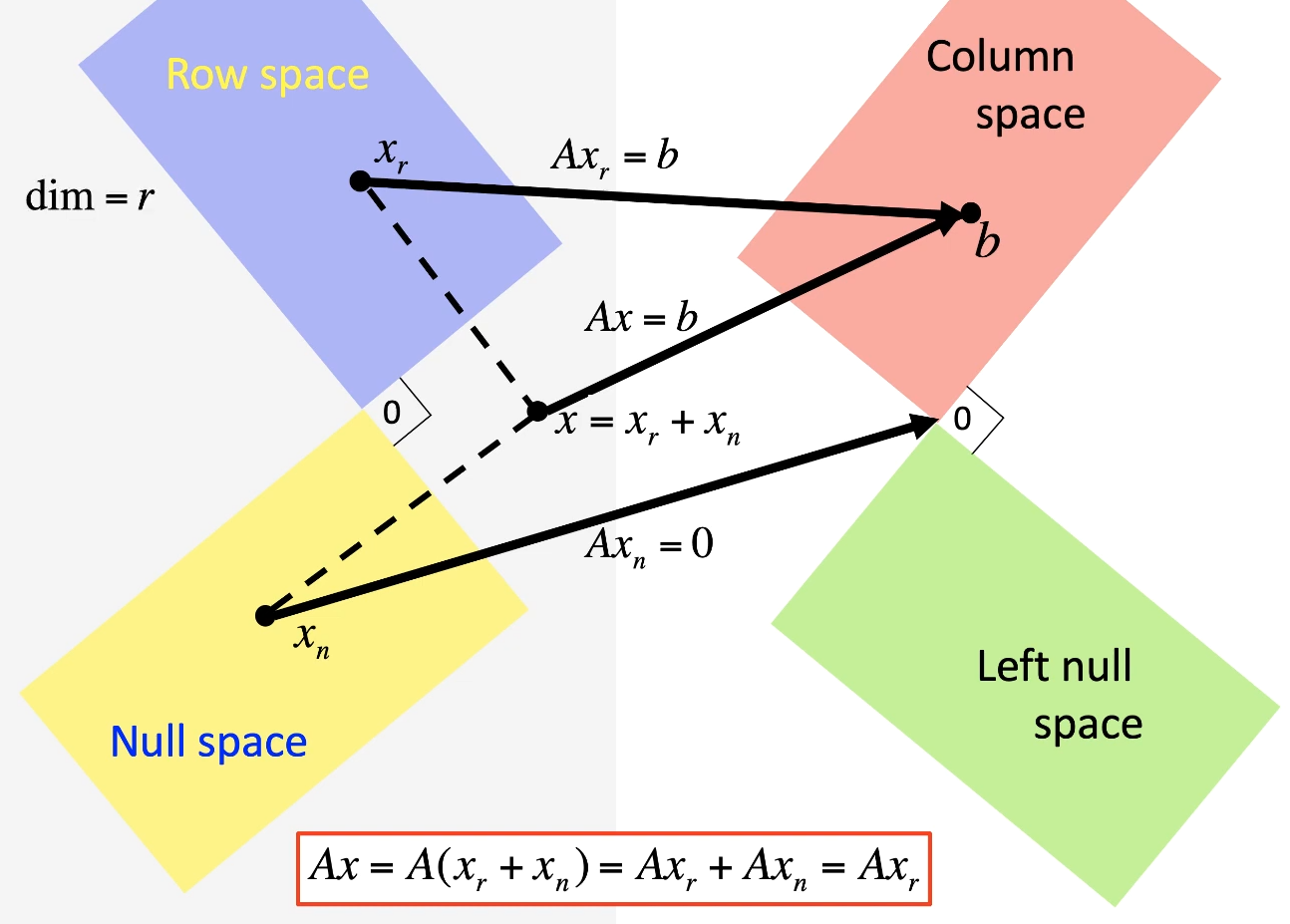Row Space里面那部分被映射到Col Space, 而Null Space里面那部分则被映射到0.

线性代数有好多看待问题的角度, 对于不同的问题, 不同角度来看是很不一样的. 比如我们有线性变换的角度, 坐标的角度, 内积外积的角度, 矩阵相乘的角度…… 对于每一个问题, 从多个角度去想一想