MIT_18.065-Part_6-Orthonormal Columns in Q Give Q'Q = I
# Orthonormal Columns in Q Give Q’Q = I
Tags: #Math/LinearAlgebra
orthogonal: 正交的 orthonormal: Ortho(gonal) + normal, 即又正交又是单位向量, 长度为1.
# Orthogonal Vectors
内积的向量化表示: $\boldsymbol{x}^{\mathrm{T}} \boldsymbol{y}=x_{1} y_{1}+\cdots+x_{n} y_{n}=0$
需要注意的是, 如果是复数相连的内积, 我们需要使用共轭复数(Conjugate)组成的向量来计算内积: $\overline{\boldsymbol{x}}^{\mathrm{T}} \boldsymbol{y}=\bar{x}{1} y{1}+\cdots+\bar{x}{n} y{n}=0$
# 与勾股定理的联系
$$\begin{aligned}||x-y||^2&=(x-y)^T(x-y)\&=x^Tx+y^Ty-x^Ty-y^Tx\&=||x||^2+||y||^2-2||x||\space ||y||cos\theta\end{aligned}$$
- x y正交的时候 $cos\theta=0$,
# Orthogonal Matrix
有了向量相互正交的表示, 我们可以很容易的推广到矩阵:
如果一个矩阵的行向量和向量x正交, 那么有$Ax=0$, 这正是前面的核空间$Null(A)$
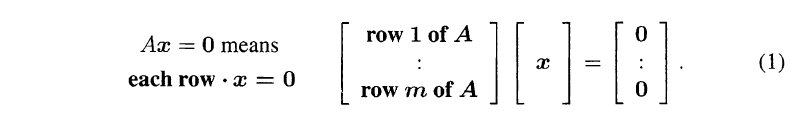
如果矩阵Q的列是单位正交的(Orthonormal), 那么有:
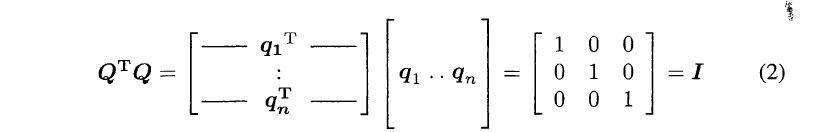
- 注意这个矩阵不一定是方阵, 它可以是一个又高又瘦的矩阵
矩阵Q有Orthonormal的列向量, 那么Q代表的线性变换不改变向量的长度, 这一点很有用.
- 证明:
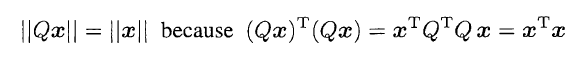
- Computations with Q never overflow!
- 证明:
如果Q是一个方阵的话, $Q^{\mathrm{T}} Q=I$ 说明 $Q^{\mathrm{T}}=Q^{-1}$, 这也说明 $QQ^{\mathrm{T}}=I$
- 但是要是Q是一个又高又瘦的矩阵 (m>n), 那么因为m个列向量不可能是正交的(因为正交向量不可能多于矩阵的秩), 所以大小为$m\times m$的矩阵$QQ^{\mathrm{T}}\neq I$
“Orthogonal matrices” are square with orthonormal columns: $Q^{\mathrm{T}}=Q^{-1}$
- 所以"Orthogonal matrices"其实叫"Orthonormal matrices"更合适
$$Orthogonal\space matrix: Q^{\mathrm{T}} Q=QQ^{\mathrm{T}}=I_{n\times n}$$
# 重要矩阵列举
# Rotation Matrix & Reflection Matrix
$$Q_{\text {rotate }}=\left[\begin{array}{rr} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]=\text { rotation through an angle } \theta$$
$$Q_{\text {reflect }}=\left[\begin{array}{rr}
\cos \theta & \sin \theta \\ \sin \theta & -\cos \theta
\end{array}\right]=\text { reflection across the } \frac{\theta}{2}\text { line. }$$
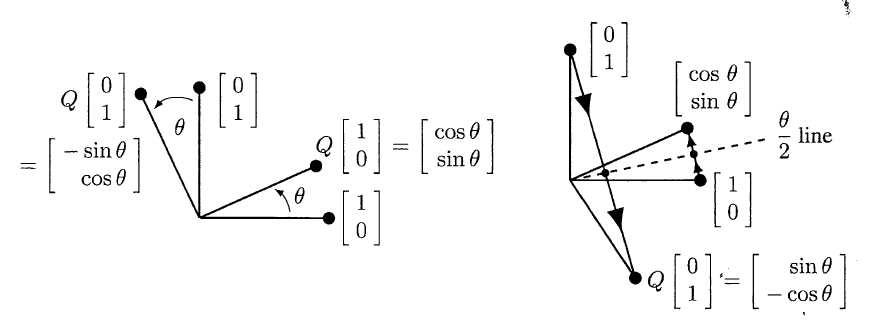
并且正规矩阵的积也是正规矩阵: $$Q_{1} Q_{2} \text { is orthogonal: } \quad\left(Q_{1} Q_{2}\right)^{\mathrm{T}}\left(Q_{1} Q_{2}\right)=Q_{2}^{\mathrm{T}} Q_{1}^{\mathrm{T}} Q_{1} Q_{2}=Q_{2}^{\mathrm{T}} Q_{2}=I$$
Rotation $\times$ rotation = rotation.
Reflection $\times$ reflection = rotation.
Rotation$\times$ reflection = reflection
# Hadamard matrices

# Householder Reflections
Why It’s Called Reflection? Watch the vid below: Householder transformations, part 1 - YouTube $$H_{n}=I-2 u u^{\mathrm{T}}$$
H是一个矩阵, 这个矩阵表示这样的一个线性变换:
- 求向量x与某个超平面的对称向量
- 哪个超平面? 单位法向量为$u$的超平面
$H_n$是一个对称矩阵, 有: $$\boldsymbol{H}^{\mathrm{T}} \boldsymbol{H}= \boldsymbol{H}^{\mathbf{2}}= \left(I-2 \boldsymbol{u} \boldsymbol{u}^{\mathrm{T}}\right) \left(I-2 \boldsymbol{u} \boldsymbol{u}^{\mathrm{T}}\right)= I-4 \boldsymbol{u} \boldsymbol{u}^{\mathrm{T}}+ 4\boldsymbol{u}\boldsymbol{u}^{\mathrm{T}}\boldsymbol{u}\boldsymbol{u}^{\mathrm{T}}=\boldsymbol{I}$$
如果我们选这一个单位向量: $u = (1, 1, … , 1)/ \sqrt n$
- 那么 $$H_n=I-2 u u^{\mathrm{T}}=I-\frac 2 n \mathrm{ones(n,n)}$$
两个例子: $$\boldsymbol{H}{3}=I-\frac{2}{3} \text { ones }=\frac{1}{3}\left[\begin{array}{rrr} 1 & -2 & -2 \\ -2 & 1 & -2 \\ -2 & -2 & 1 \end{array}\right] \quad \boldsymbol{H}{4}=I-\frac{2}{4} \text { ones }=\frac{1}{2}\left[\begin{array}{rrrr} \mathbf{1} & -1 & -1 & -1 \\ -1 & \mathbf{1} & -1 & -1 \\ -1 & -1 & \mathbf{1} & -1 \\ -1 & -1 & -1 & \mathbf{1} \end{array}\right]$$
- 关于特征值这一点还不是很理解: The “eigenvalues” of H are -1 (once) and +1 (n- 1 times). All reflection matrices have eigenvalues -1 and 1.
# Haar wavelets
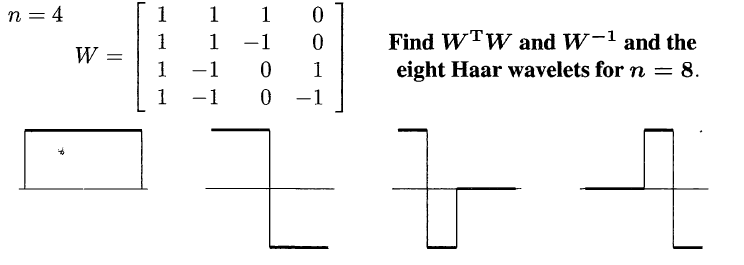 n=8
$$\left[\begin{array}{ccc}1&1&1&&1&&&\\ 1&1&1&&-1&&&\\ 1&1&-1&&&1&&\\ 1&1&-1&&&-1&&\\ 1&-1&&1&&&1&\\ 1&-1&&1&&&-1&\\ 1&-1&&-1&&&&1\\ 1&-1&&-1&&&&-1\end{array}\right]$$
n=8
$$\left[\begin{array}{ccc}1&1&1&&1&&&\\ 1&1&1&&-1&&&\\ 1&1&-1&&&1&&\\ 1&1&-1&&&-1&&\\ 1&-1&&1&&&1&\\ 1&-1&&1&&&-1&\\ 1&-1&&-1&&&&1\\ 1&-1&&-1&&&&-1\end{array}\right]$$
# Eigenvectors of $S=S^T$ & $Q^TQ=I$
- The Eigenvectors of a Symmetric Matrix and an Orthogonal Matrix is Orthogonal.
- 一个例子是下面的矩阵P的特征向量构成了 4 by 4 Fourier matrix F. $$P=\left[\begin{array}{llll} 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 \end{array}\right]$$ $$F=\left[\begin{array}{ccrr} 1 & 1 & 1 & 1 \\ 1 & i & i_2 & i^3 \\ 1 & i^{2} & i_4 & i^6 \\ 1 & i^{3} & i^6 & i^9 \end{array}\right]$$ 下面的矩阵Q有orthonormal的列向量: $$Q=\frac{F}{2}=\frac{1}{2}\left[\begin{array}{ccrr} 1 & 1 & 1 & 1 \\ 1 & i & -1 & -i \\ 1 & i^{2} & 1 & -1 \\ 1 & i^{3} & -1 & i \end{array}\right]$$
注意复数的内积需要取共轭: 验证, 对于F, 第二列和第四列的内积: $[1,-i,i^2,-i^3]\left[\begin{array}{ccrr}1 \i^3 \i^6 \\ i^9\end{array}\right]=1-1+1-1=0$
# 每一个向量空间$R^n$都有一组正交基
这可以由Gram-Schmidt方法得到
奇异值分解可以找到矩阵$A$的$Row\space Space$的一组正交基: $u_1\cdots u_r$, 矩阵$A$的$Column\space Space$的一组正交基: $v_1\cdots v_r$, 其中r是A的秩.
- 这个两个正交基特殊的地方在于它们由矩阵A联系起来:
$$\text { Singular vectors } \quad A \boldsymbol{v}{1}=\sigma{1} \boldsymbol{u}{1} \quad A \boldsymbol{v}{2}=\sigma_{2} \boldsymbol{u}{2} \quad \cdots \quad A \boldsymbol{v}{r}=\sigma_{r} \boldsymbol{u}_{r}$$
- For the bases from the SVD, multiplying by A takes an orthogonal basis of v’s to an orthogonal basis of u’s.
# 投影矩阵

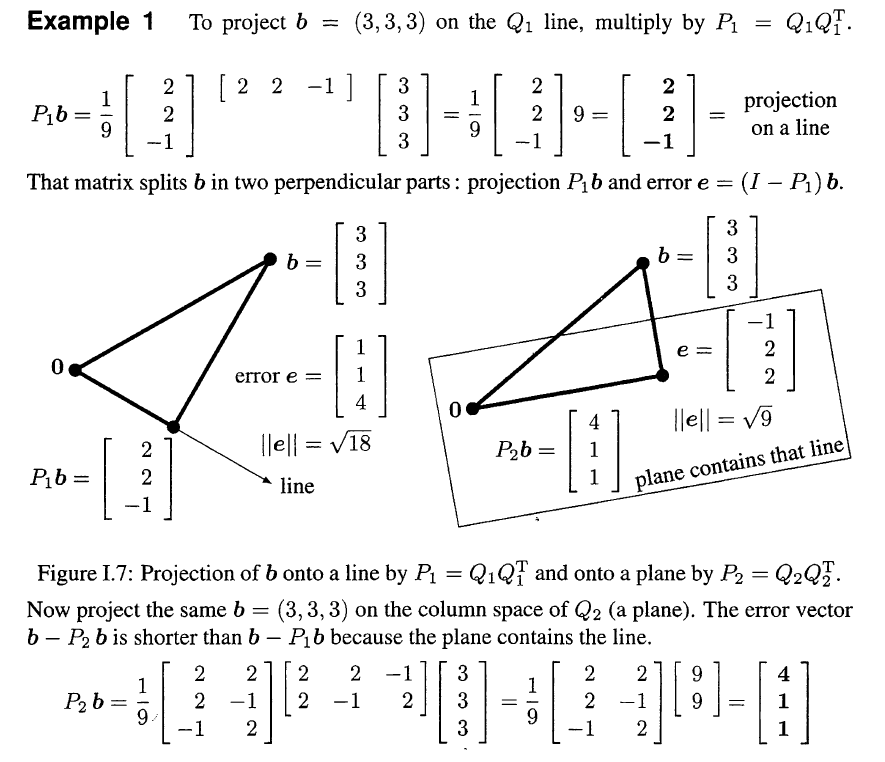

$$Px=QQ^{\mathrm{T}}x=Q(Q^{\mathrm{T}}x)=$$ $$Col(Q)(Inner\space product\space of\space Row(Q)\space and\space x)$$ 就是先计算x与Q里面各个正交基底的内积, 得到在这个正交基底下的"坐标", 然后再用Col(Q)表示出来.