MIT_18.065-Part_7-Eigenvalues and Eigenvectors
# Eigenvalues and Eigenvectors
Tags: #Math/LinearAlgebra #Math/LinearAlgebra/Eigenvalue
# 特征值的一些性质
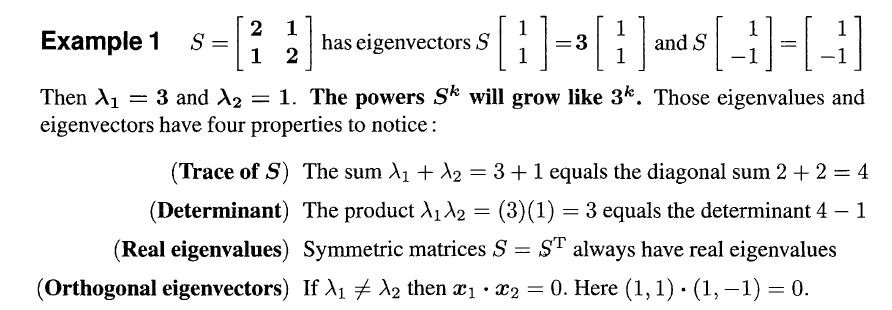
# 相似矩阵
# 相似矩阵有相同的特征值
$$P^{-1}AP = B$$ 假设矩阵$B$有特征值$\lambda$: $$Bx=\lambda x$$ 则 $$\begin{aligned}P^{-1}APx&=\lambda x \\ &\Rightarrow \\ APx&=P\lambda x \\ &\Rightarrow \\ A(Px)&=\lambda (Px)\end{aligned}$$
A也有特征值$\lambda$, 对应特征向量$Px$
- 而且$Px$刚好是 把B里面的特征向量x 通过基变换矩阵P 转换到A的坐标下.
# Symmetric Matrix: $S=S^T$
# S have Real Eigenvalues
See the document below: Symmetric matrices have real eigenvalues
# S have Orthogonal Eigenvectors
This is a good video, 视频的开头同时也说明了Eigenvalue可能遇到的"Defective Case" Eigenvectors of Symmetric Matrices Are Orthogonal - YouTube
首先, 对于实对称矩阵S, 有$S=S^T$
对于不同的两个特征值$\lambda_1, \lambda_2$, 有 $$\begin{aligned}Sx&=\lambda_1 x\Sy&=\lambda_2 y\end{aligned}$$
我们做下面的变形, 将两边都变成内积: $$\begin{aligned}y^TSx&=\lambda_1y^T x\\ x^TSy&=\lambda_2x^T y\end{aligned}$$
对于第一个式子的左边, 因为是$y^T$与$Sx$的内积, 是一个数, 其转置还是自己: $$(y^TSx)^T=x^TS^Ty=x^TSy=\text{第二个式子的左边}$$
两式相减, 所以有: $$0=(\lambda_1-\lambda_2)x^T y=(\lambda_1-\lambda_2)x\cdot y$$
因为假设特征值是不相同的, 所以x与y的内积为0, 所以任意两个特征向量相互垂直.
注意: 有的特征空间可能是多维的, 但是在这个特征空间里面也可以找到一个正交的基, 并且其他特征空间里面的特征向量是和这个特征空间垂直的, 自然也和这个正交的基垂直.
- 综上: 实对称矩阵是一个很特殊的矩阵, 它只有实特征值, 并且特征向量都是相互正交的.
- 这是一种找正交矩阵的很方便的方法
# 对角化矩阵

对于对称矩阵, 则更为特殊: $$S=Q\Lambda Q^{-1}$$ 因为对称矩阵的特征向量都是正交的, 我们有$Q^T=Q^{-1}$: $$S=Q\Lambda Q^{T}$$
- $S=Q\Lambda Q^{T}$也被称为"Spectral Theorem"(谱定理) ^a919e0
每一个实对称矩阵由两部分组成: 相互正交的特征向量组成的Q和实特征值组成的对角矩阵$\Lambda$