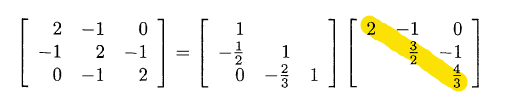MIT_18.065-Part_8-Positive Definite and Semidefinite Matrices
# Positive Definite and Semi-definite Matrices
Tags: #Math/LinearAlgebra
- Positive Definite Matrices are the Best of the Symmetric Matrices.
# 五个判别条件
- 同时也是正定矩阵的重要性质:
- Positive Eigenvalues
- 所有的特征值都是正数
- Energy $x^TSx>0$, $\forall x\neq 0$
- 有正的"能量", 这点后面会详述
- $S=A^TA$, A has Independent Columns
- S可以被分解为一个矩阵的转置与自己的乘积
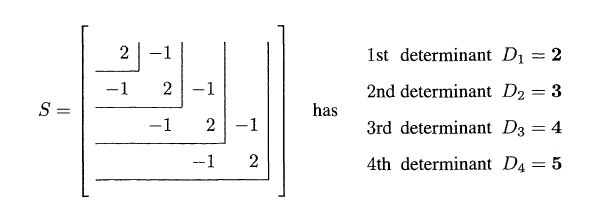
- All leading Determinants > 0
- All Pivots in Elimination > 0
# Energy
(在视频里面没有找到详细的定义, 网上也没有相关的资料, 应当是一个直观的概念)
“能量"在这里体现为一种"二次(quadratic)“的概念, 比如在动能, 势能等定义里面, 都有二次项的存在.
x里面的能量通过计算$x^TSx$来得出, 类似于内积, 但是中间多了一个$S$
以正定矩阵$$\left[\begin{array}{ll} 2 & 4 \\ 4 & 9 \end{array}\right]$$为例:
$$[x, y]\left[\begin{array}{ll} 2 & 4 \\ 4 & 9 \end{array}\right]\left[\begin{array}{l} x \\ y \end{array}\right]=f(x, y)$$ $$\begin{align}&=2x^2+9y^2+4xy+4yx\&=2x^2+9y^2+8xy\&=2(x+2y)^2+y^2>0 \end{align}$$
- 为什么能量大于零, 这个矩阵就是正定的呢? 首先, 对于特征向量: $$\text { If } S x=\lambda x \text { then } x^{\mathrm{T}} S x=\lambda x^{\mathrm{T}} x \text {. So } \lambda>0 \text { leads to } x^{\mathrm{T}} S x>0 \text {. }$$
- 而在正规矩阵里面特征向量可以表示任意向量x, (因为它们构成一组正交基底):
$$\begin{aligned}
\boldsymbol{x}^{\mathrm{T}} S \boldsymbol{x} &=\left(c_{1} \boldsymbol{x}{1}^{\mathrm{T}}+\cdots+c{n} \boldsymbol{x}{n}^{\mathrm{T}}\right) S\left(c{1} \boldsymbol{x}{1}+\cdots+c{n} \boldsymbol{x}{n}\right) \\ &=\left(c{1} \boldsymbol{x}{1}^{\mathrm{T}}+\cdots+c{n} \boldsymbol{x}{n}^{\mathrm{T}}\right)\left(c{1} \lambda_{1} \boldsymbol{x}{1}+\cdots+c{n} \lambda_{n} \boldsymbol{x}{n}\right) \\ &=c{1}^{2} \lambda_{1} \boldsymbol{x}{1}^{\mathrm{T}} \boldsymbol{x}{1}+\cdots+c_{n}^{2} \lambda_{n} \boldsymbol{x}{n}^{\mathrm{T}} \boldsymbol{x}{n}>\mathbf{0} \text { if every } \boldsymbol{\lambda}_{i}>\mathbf{0}
\end{aligned}$$
可以看到正定矩阵里面的对角线元素对应二次项, 而其他元素对应交叉项.
这个函数的图像如下图所示:
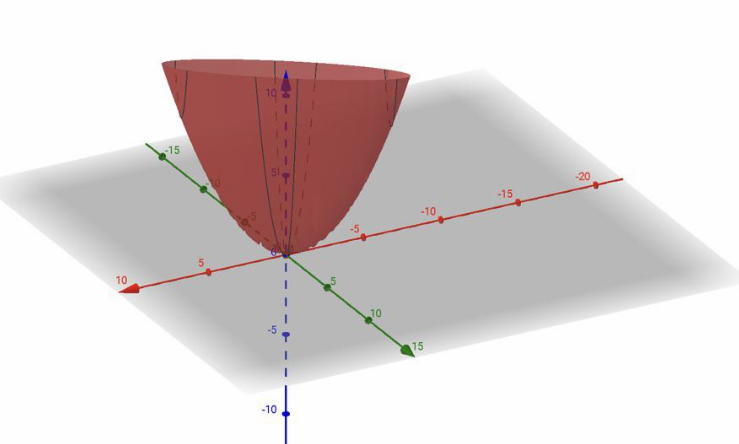
而这与机器学习里面的损失函数有着密切的联系: 最小化损失 <=> 最小化能量 Cost_Function_Intuition
- 如果一个函数是严格凸的, 那么它的二阶导数矩阵在每一点都是正定的.
- 对于极小值:
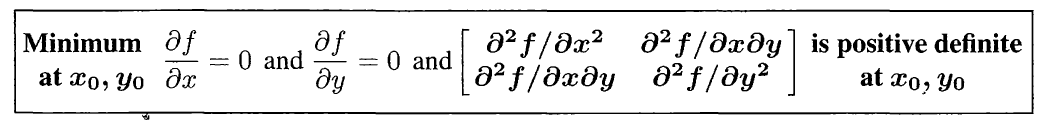
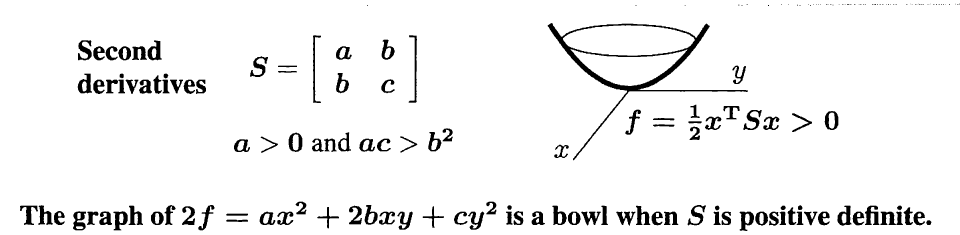如果矩阵S有负的特征值, 那么f的图像会在0以下. 在S是负定的时候(所有特征值都是负的), 与正定的时候相反, 函数会有最大值. 函数有的特征值大于零有的小于零, 那么它会有"鞍点”, A saddle point matrix is “indefinite”.
# 半正定矩阵
Semi-definite allows energy / eigenvalues / determinants / pivots of S to be zero.
第三点里面也允许不独立的列
见视频里面的这段:
# $S=A^TA$
$S=A^TA$容易知道是一个对称矩阵, 在这个情况下:
$$Energy=x^TSx=x^TA^TAx = (Ax)^TAx= ||Ax||^2\geq0$$
- 所以S一定是正定或者半正定的
当A有线性相关的列的时候, Ax可以=0, 这个时候S为半正定矩阵.