MIT_18.065-Part_9-Singular Value Decomposition-SVD

Last updated Nov 14, 2021 Edit Source

• All
• Math linear algebra
• Svd

Tags: #Math/LinearAlgebra #SVD

¹

• SVD将任意矩阵$A$分解成了三个部分:
  • $U$ 的列是相互正交的. - Left Singular Vectors
  • $\Sigma$ 的对角线上面是递减的奇异值. - Singular Values
  • $V^T$ 的行是相互正交的. - Right Singular Vectors

在最棒的情况下, 我们的矩阵是一个实对称矩阵$S$: 它有实特征值和正交的特征向量. 根据 谱定理, 我们能够将这个矩阵分解成以下形式: $$S=Q\Lambda Q^T$$

但是在很多情况下, 我们的特征空间并没有那么大, 所以我们需要将上述分解进行一些推广. SVD便是一种优美的推广形式:

$$A=U\Sigma V^T$$

²

• 完整形式的SVD长这样: $$A_{m\times n}=U_{m\times m}\Sigma_{m\times n}V^T_{n\times n}$$

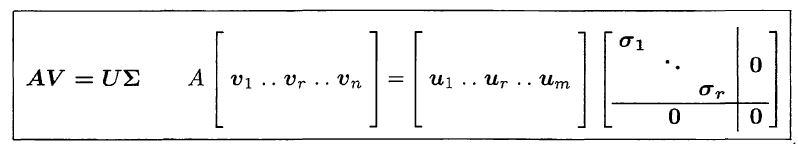
这样的话有许多"没用的部分": $\Sigma$里面有很多零, 并且U, V里面有许多零空间里面的向量(后面会解释). 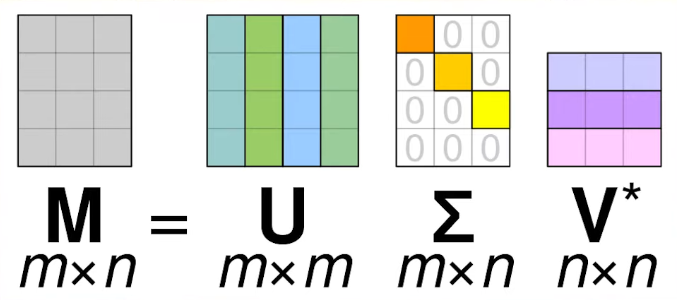³

• 精简版的SVD长这样(The Reduced Form):

$$A_{m\times n}=U_{m\times r}\Sigma_{r\times r}V^T_{r\times n}$$ 其中$r$是矩阵$A$的秩 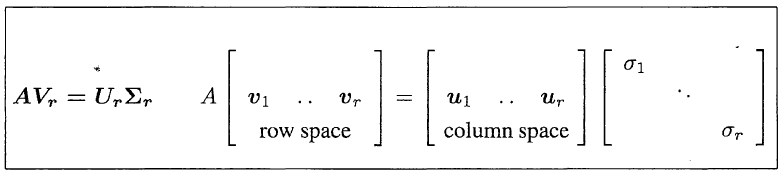这是$\Sigma$是一个对角矩阵了, 并且$V, U$只包含"有用的特征向量"了

关于特征值的一个结论 关于秩的一个结论 $S=A^TA$至少是半正定的, 所以它的特征值一定是非负的

⁴

证明和矩阵$A^TA$与$AA^T$有着紧密的联系:

• 容易知道$A^TA$与$AA^T$都是对称矩阵:
  • $A^TA$是$Col(A)$相互乘, $AA^T$是$Row(A)$相互乘

根据对称矩阵的 谱定理这个良好的性质, 我们可以得到下面的这两个分解: $$\begin{aligned} &A^\mathrm{T} A= V \Sigma_1 V^{\mathrm{T}} \\ &A A^\mathrm{T}=U \Sigma_2 U^{\mathrm{T}} \end{aligned}$$

• 其中$V,U$均为正交矩阵, 为$A^\mathrm{T} A$和$AA^\mathrm{T}$的特征向量.

如果我们假设SVD这个分解是成立的, 那么我们可以得到如下分解: $$\begin{aligned} &A^\mathrm{T} A=(V \Sigma^\mathrm{T} U^\mathrm{T})(U \Sigma V^\mathrm{T}) = V \Sigma^2 V^\mathrm{T} \\ &A A^\mathrm{T}=(U \Sigma V^\mathrm{T})(V \Sigma^\mathrm{T} U^\mathrm{T})=U \Sigma^2 U^\mathrm{T} \end{aligned}$$ 可以猜想, 上下两个等式的$V,U,\Sigma$ 都是对应的, 后面我们将会证明这是成立的, 即:

• SVD分解$A=U\Sigma V^T$里面的
  • $V^T$的行向量是$A^\mathrm{T} A$的特征向量, 它们orthonormal
  • $U$的列向量是$AA^\mathrm{T}$的特征向量, 它们orthonormal
  • $\sigma^2_1$ 到 $\sigma^2_r$ 是 $A^TA$ 与 $AA^T$ 的非零特征值, 后面会详细叙述.

我们下一步将证明$A$将这两组正交向量$U,V$一一联系起来, 即: $$A v_{k}=\sigma_{k} u_{k}$$

观察我们上面的猜想, 我们假设$\sigma_{k}=\sqrt{\lambda_{k}}$, 选择$A^TA$单位正交的一组特征向量$v_1, \cdots v_r$

• 因为$v_k$是$A^\mathrm{T} A$的特征向量, 所以有 $$A^{\mathbf{T}} A v_{k}=\sigma_{k}^{2} v_{k}$$
• 根据证明的目标$A v_{k}=\sigma_{k} u_{k}$, 我们构造 $$u_{k}=\frac{A v_{k}}{\sigma_{k}}$$
• 下面我们只需要证明$u_k$也是$A A^\mathrm{T}$单位正交的特征向量即可:
  • 证明是特征向量: $$AA^\mathbf{T}\boldsymbol{u}{k}= AA^{\mathrm{T}}\left(\frac{A\boldsymbol{v}{k}}{\sigma_{k}}\right)= A\left(\frac{A^\mathrm{T}A \boldsymbol{v}{k}}{\sigma{k}}\right)= A\frac{\sigma_{k}^{2} \boldsymbol{v}{k}}{\sigma{k}}= \sigma_{k}^{2} \boldsymbol{u}{k}=\lambda_k\boldsymbol{u}{k}$$
  • 证明单位正交: $$\boldsymbol{u}{j}^{\mathrm{T}} \boldsymbol{u}{k}=\left(\frac{A \boldsymbol{v}{j}}{\sigma{j}}\right)^{\mathrm{T}}\left(\frac{A \boldsymbol{v}{k}}{\sigma{k}}\right)=\frac{\boldsymbol{v}{j}^{\mathrm{T}}\left(A^{\mathrm{T}} A \boldsymbol{v}{k}\right)}{\sigma_{j} \sigma_{k}}=\frac{\sigma_{k}}{\sigma_{j}} \boldsymbol{v}{j}^{\mathrm{T}} \boldsymbol{v}{k}= \begin{cases}1 & \text { if } j=k \\ 0 & \text { if } j \neq k\end{cases}$$

如果我们证明的是缩减形式的SVD, 那么证明已经结束了, 如果证明的是一般形式的SVD, 那么需要将矩阵$U, V$补全:

• 对于$V_{n\times n}$我们可以从$Null(A)$里面选择相互正交的$n-r$个向量$v_{r+1}, \cdots v_n$来补足正交向量
• 对于$U_{m\times m}$我们可以从$Null(A^T)$里面选择相互正交的$m-r$个向量$u_{r+1}, \cdots u_m$来补足正交向量

因为核空间$Null(A)$和$Row(A)$相互正交, ${v_1, \cdots v_r}\subset Row(A)$, $Null(A^T)$和$Col(A)$相互正交, ${u_1, \cdots u_r}\subset Col(A)$, 所以补足后的正交向量依然相互正交.

这样, 我们就证明了SVD.

• $AV=U\Sigma$说明了, A将一个正交基底$V$映射到$U$, 而$U$依然是正交的

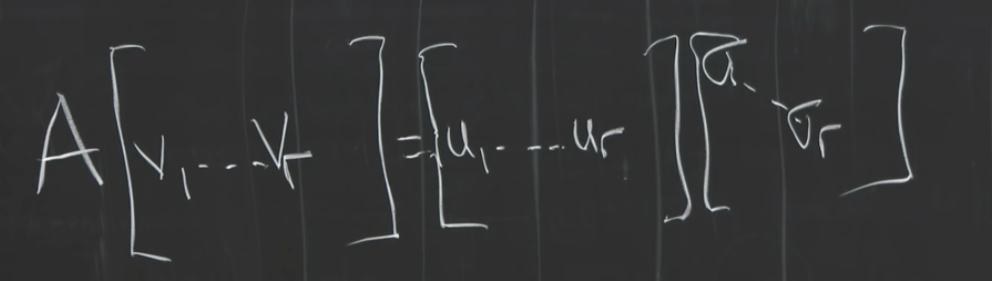
这个视频的开头部分演示了这个视角:

The eigenvectors give $AX = XA$. But $AV = U\Sigma$: needs two sets of singular vectors.

• Right Singular vectors in $V$ contains orthonormal eigenvectors of $A^T A$
  • 因为$A^T A$在A的Row Space里面, V包含了Row(A)的信息
• Left Singular vectors in $U$ contains orthonormal eigenvectors of $AA^T$
  • 因为$AA^T$在A的Column Space里面, U包含了Col(A)的信息
• $\sigma_1^2$ to $\sigma_r^2$ are the nonzero eigenvalues of both $A^T A$ and $AA^T$
  • 奇异值包含的信息则是不同特征向量的"重要性"

⁵ 上面这个视频的重点是:$AA^T$, $A^TA$是有实际含义的: Correlation Matrix

• U和V是两个相关矩阵的特征值

• $U$: “Eigen-Faces”

• $V$: “Eigen-Time”/“Eigen-Composition”

Sum of Rank 1 Matrices: Different Importance

• Why is the SVD so important for this subject and this book? Like the other factorizations A = LU and A = QR and $S = Q\Lambda Q^T$, it separates the matrix into rank one pieces.
• A special property of the SVD is that those pieces come in order of importance.
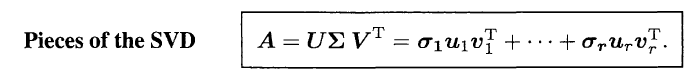
• The first piece of $\sigma_1 u_1 v_1^T$ is the closest rank one matrix to $A$. More than that is true: The sum of the first k pieces is best possible for rank k: $$A_{k}=\sigma_{1} u_{1} v_{1}^{\mathrm{T}}+\cdots+\sigma_{k} u_{k} v_{k}^{\mathrm{T}}$$

下面这个演示也是这个视角, 这是PCA里面的主要视角 SVD Intuition

A Fancy Example of SVD

SVD Intuition

• 关于SVD网上有很多很棒的讲解与演示, 这是一个很有趣也很重要的主题.