Bayesian Decision Theory - Part1

Last updated Dec 21, 2021 Edit Source

• All
• Machine learning
• Bayes

Tags: #MachineLearning #Bayes

• 贝叶斯决策其实就是把生活中我们基于直觉和常识的决策方法形式化了, 并加以进一步地推广.
• 贝叶斯决策综合考量每种情况的概率和决策带来的代价.
• 贝叶斯决策假设问题可以用概率分布的形式来刻画, 属于贝叶斯学派的一种方法.

• 假如圣诞老人打包了100盒糖果, 其中20盒是巧克力($\omega_1$), 80盒是水果硬糖($\omega_2$), 现在他从里面随机挑了一盒给小企鹅, 盒子的颜色和重量都一样, 那么小企鹅得到的是巧克力还是水果硬糖呢?
  • 如果我们猜对了, 就可以得到一盒糖果!
• 因为我们只知道不同礼物的比例, 也就是$P(\omega_1)=0.2, P(\omega_2)=0.8$, 所以为了使正确的概率最大, 我们应该猜礼物是 $\omega_2$.
• 但是要是圣诞老人要给整个南极洲的企鹅每人一个礼物呢? 如果我们一直猜, 为了获得更多的糖果, 我们只能一直猜礼物是 $\omega_2$ ! 这显然太傻了.

• 幸运的是, 我们发现了规律, 圣诞老人会根据小企鹅的体重($x$)来发放不同的礼物, 越胖的小企鹅越不容易得到巧克力($\omega_1$).

• 假设我们给所有已经有了礼物的小企鹅都称了一遍体重, 并且偷偷看了它们的礼物是什么. 现在我们知道了"机密": 不同礼物小企鹅的体重分布情况$P(x\mid \omega_i)$

• 我们又从官方手册上查到了小企鹅的体重分布情况$P(x)$.

• 现在圣诞老人又来给小企鹅发糖果了! 但是现在我们可以先偷偷给小企鹅称体重, 再猜它们会得到什么礼物. 假设下一只小企鹅"Pupu"的体重为$x$:

• 根据Bayes定理: $$P(\omega_i \mid x)=\frac{P(x\mid \omega_i) P(\omega_i)} {P(x)}$$ 也就是: $$postprior=\frac{likelihood\times prior}{evidence}$$

  • 后验概率$postprior$就是我们综合所有信息后作出的决策: 如果$P(\omega_1 \mid x)>P(\omega_2 \mid x)$, 那么说明Pupu更可能得到巧克力, 反之亦然
  • $likelihood$就是我们掌握的"机密": 礼物已知的体重分布关系$P(x\mid \omega_i)$.
  • $evidence$是我们的"线索": Pupu的体重.
  • $prior$就是圣诞老人告诉我们的礼物组成: 20%的巧克力, 80%的水果硬糖.

• 可以看到, 我们现在能够更聪明地作出决策了! 我们通过小企鹅的体重$x$, 综合 prior 分布和 likelihood 分布得到了一个更聪明的分布: postprior 分布. 也就是说, 我们综合考虑了"胖企鹅得不到巧克力" 和 “巧克力有多少”, 而不是像之前那样一直猜同一个东西. 这就是贝叶斯决策的主要思想.

• 因为在决策的时候我们关心的只有$\omega_1$还是$\omega_2$的概率大. 所以可以把分母上的evidence: $P(x)$看作一个比例系数, 作用是让x所有取值下的$P(\omega_i \mid x)$加起来为 1. 而真正和决策对象$\omega$有关的只是分子上的$P(x\mid \omega_i) P(\omega_i)$

• 下面我们用更形式化的方法来介绍贝叶斯决策的进一步推广.

• 有的时候不同的选择的代价是不一样的, 我们可以定量地刻画代价的不同, 并在决策的时候进行综合考虑:

  • 我们令$\lambda\left(\alpha_{i} \mid \omega_{j}\right)$为实际类别为$\omega_{j}$的时候采取行动$\alpha_{i}$的代价, 通常当$i=j$的时候这个值较小.
  • 那么采取行动$\alpha_{i}$的总体代价可以表示为: $$R\left(\alpha_{i} \mid \mathbf{x}\right)=\sum_{j=1}^{c} \lambda\left(\alpha_{i} \mid \omega_{j}\right) P\left(\omega_{j} \mid \mathbf{x}\right)$$ $R\left(\alpha_{i} \mid \mathbf{x}\right)$也被称为条件风险.
  • 更进一步, 对于任意的$\mathbf{x}$, 我们的决策规则可以抽象为一个函数$\alpha(\mathbf{x})$, 自动给出情况$\mathbf{x}$下最优的决策方案$\alpha_i$. 所以情况$\mathbf{x}$下的"加权风险"可以表示为: $$R(\alpha(\mathbf{x}) \mid \mathbf{x}) p(\mathbf{x})$$
  • 综合下来, 对于所有可能的$\mathbf{x}$, 整个决策方案的风险为: $$R=\int R(\alpha(\mathbf{x}) \mid \mathbf{x}) p(\mathbf{x}) d \mathbf{x}$$ 这就是我们想要最小化的东西.

• 最小的代价也叫贝叶斯风险(Bayes risk), 是整个决策方案所能够达到的最佳水平.

二分类问题两个决策的代价可以表示如下: $$\begin{aligned} &R\left(\alpha_{1} \mid \mathbf{x}\right)=\lambda_{11} P\left(\omega_{1} \mid \mathbf{x}\right)+\lambda_{12} P\left(\omega_{2} \mid \mathbf{x}\right) \\ &R\left(\alpha_{2} \mid \mathbf{x}\right)=\lambda_{21} P\left(\omega_{1} \mid \mathbf{x}\right)+\lambda_{22} P\left(\omega_{2} \mid \mathbf{x}\right) \end{aligned}$$

• 当然, 如果$R\left(\alpha_{1} \mid \mathbf{x}\right)<R\left(\alpha_{2} \mid \mathbf{x}\right)$, 我们会选择$\alpha_1$, 因为此时风险更小.
• 换个形式, 也就是$$\left(\lambda_{21}-\lambda_{11}\right) P\left(\omega_{1} \mid \mathbf{x}\right)>\left(\lambda_{12}-\lambda_{22}\right) P\left(\omega_{2} \mid \mathbf{x}\right)$$或者$$\left(\lambda_{21}-\lambda_{11}\right) p\left(\mathbf{x} \mid \omega_{1}\right) P\left(\omega_{1}\right)>\left(\lambda_{12}-\lambda_{22}\right) p\left(\mathbf{x} \mid \omega_{2}\right) P\left(\omega_{2}\right)$$时选择方案1.
• 我们也可以表示为分数的形式:$$\frac{p\left(\mathbf{x} \mid \omega_{1}\right)}{p\left(\mathbf{x} \mid \omega_{2}\right)} >\frac{\lambda_{12}-\lambda_{22}}{\lambda_{21}-\lambda_{11}} \frac{P\left(\omega_{2}\right)}{P\left(\omega_{1}\right)}$$这时决策指标$\frac{p\left(\mathbf{x} \mid \omega_{1}\right)}{p\left(\mathbf{x} \mid \omega_{2}\right)}$为一个数$\theta$, 称为likelihood ratio(似然比). 这时控制决策边界的重要参数: 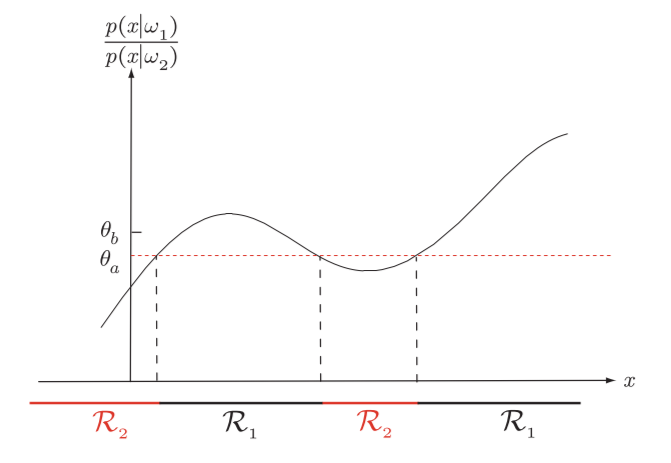在上面这个图中, 如果将$\omega_2$误判为$\omega_2$的代价更大, 即 $\lambda_{12}>\lambda_{21}$ . 那么会导致$\theta$上升到$\theta_b$, 即$\mathcal{R}_{1}$变小, 判断为$\omega_1$的情况表少.

• 二分类情况下, 一次决策的误差率可以表示为$$P(\text { error } \mid x)= \begin{cases}P\left(\omega_{1} \mid x\right) & \text { if we decide } \omega_{2} \\ P\left(\omega_{2} \mid x\right) & \text { if we decide } \omega_{1}\end{cases}$$

• 总的情况下, 平均误差率可以表示为:$$P(\text { error })=\int_{-\infty}^{\infty} P(\text { error }, x) d x=\int_{-\infty}^{\infty} P(\text { error } \mid x) p(x) d x$$

• 为了使误差率最小, 决策方案为: Decide $\omega_{1}$ if $P\left(\omega_{1} \mid x\right)>P\left(\omega_{2} \mid x\right) ;$ otherwise decide $\omega_{2}$, 也就是:$$P(\text { error } \mid x)=\min \left[P\left(\omega_{1} \mid x\right), P\left(\omega_{2} \mid x\right)\right]$$

• 在很多情况下, 我们会希望误判的次数最少, 即误差率最小. 我们可以这样构造损失函数来获得贝叶斯决策下的最小误差率: $$\lambda\left(\alpha_{i} \mid \omega_{j}\right)=\left{\begin{array}{ll}0 & i=j \1 & i \neq j \end{array} \quad i, j=1, \ldots, c\right.$$ 在判断正确时为0, 在其他错误情况下都为1, 故这个损失函数也称0-1损失函数.
• 我们可以证明在0-1损失函数下有着最小误差率:
  • 此时条件损失为: $$\begin{aligned} R\left(\alpha_{i} \mid \mathbf{x}\right) &=\sum_{j=1}^{c} \lambda\left(\alpha_{i} \mid \omega_{j}\right) P\left(\omega_{j} \mid \mathbf{x}\right) \\ &=\sum_{j \neq i} P\left(\omega_{j} \mid \mathbf{x}\right) \\ &=1-P\left(\omega_{i} \mid \mathbf{x}\right) \end{aligned}$$
  • 为了获得最小的总代价, 我们需要让每一个条件代价都尽可能地小, 也就是让$P(\omega_{i} \mid \mathbf{x})$尽可能大, 也就是选择$\mathbf{x}$已知时出现概率最大的$\omega_{i}$: $$P(\text { error } \mid x)=\min \left[P\left(\omega_{i} \mid x\right) \right]$$

• 有时候先验概率是不确定的, 但是likelihood是确定的, 我们希望能够在这种情况下也能够有较好的表现.

• prior是不确定的会导致最佳表现(Bayes Risk)是关于prior的一个函数, 后面我们会看到Bayes Risk $R$是关于$P(\omega_i)$的一个线性函数, 我们希望得到这个线性函数在最坏情况下的最好表现(Mini-Max, “最小的最大”)

• 怎么寻找这个"最好表现"?

  • 首先, 我们固定Prior: $P(\omega_i)$, 计算在$P(\omega_i)$不同取值下, 贝叶斯决策的最好表现(Bayes Risk), 得到下图中的拱形曲线. (下图中Bayes Risk以最小误差为例, 所以纵坐标为$P(error)$) 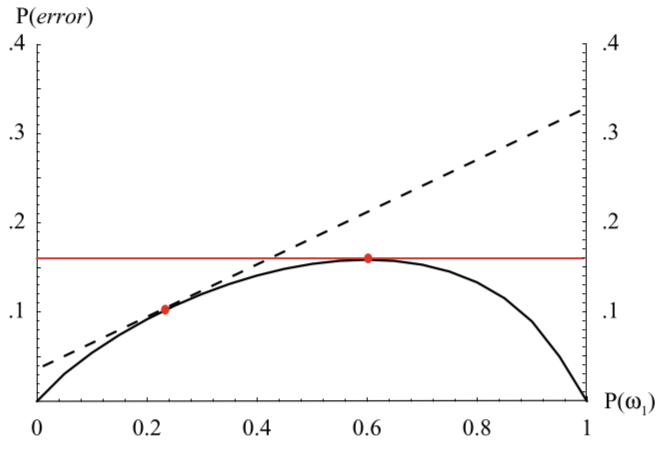可以看到, 如果先验概率不变, 在$P(\omega_1)=0.6$时, 模型有最坏的表现.
  • 在这些所有最好表现里面, 如果$P(\omega_1)$偏移了最佳情况下的取值, 那么模型误差率随着$P(\omega_1)$线性变化, 这表现为图中的虚线.
    • 在虚线代表的"最好"表现上可能发展到的"最坏"结果在$P(\omega_1)=1$时取得, 大约为0.34
  • 我们可以看到, 为了限制这个"最好表现"上可能发展到的"最坏结果", 原来在0.6取到的最差的Bayes Risk反而成为了最好的情况, 换句话说, $P(\omega_1)=0.6$时模型表现没有那么好, 但是很稳妥.
  • 模型在这一点取得的Bayes Risk即$R_{mm}$, minimax risk.

下面我们证明likelihood不变的情况下, 模型的表现随先验概率呈线性变化.

• 总的风险可以表示为:$$\begin{aligned} R &=\int_{\mathcal{R}{1}}\left[\lambda{11} P\left(\omega_{1}\right) p\left(\mathbf{x} \mid \omega_{1}\right)+\lambda_{12} P\left(\omega_{2}\right) p\left(\mathbf{x} \mid \omega_{2}\right)\right] d \mathbf{x} \\ &+\int_{\mathcal{R}{2}}\left[\lambda{21} P\left(\omega_{1}\right) p\left(\mathbf{x} \mid \omega_{1}\right)+\lambda_{22} P\left(\omega_{2}\right) p\left(\mathbf{x} \mid \omega_{2}\right)\right] d \mathbf{x} \end{aligned}$$
• 利用恒等式 $P\left(\omega_{2}\right)=1-P\left(\omega_{1}\right)$ 和 $\int_{\mathcal{R}{1}} p\left(\mathbf{x} \mid \omega{1}\right) d \mathbf{x}=1-\int_{\mathcal{R}{2}} p\left(\mathbf{x} \mid \omega{1}\right) d \mathbf{x}$ 我们可以把上式重新表示为: $$\begin{aligned} R\left(P\left(\omega_{1}\right)\right) &=\overbrace{\lambda_{22}+\left(\lambda_{12}-\lambda_{22}\right) \int_{\mathcal{R}{1}} p\left(\mathbf{x} \mid \omega{2}\right) d \mathbf{x}}^{=R_{m m}, \operatorname{minimax} \text { risk }} \\ &+P\left(\omega_{1}\right)[\underbrace{\left[\left(\lambda_{11}-\lambda_{22}\right)-\left(\lambda_{21}-\lambda_{11}\right) \int_{\mathcal{R}{2}} p\left(\mathbf{x} \mid \omega{1}\right) d \mathbf{x}-\left(\lambda_{12}-\lambda_{22}\right) \int_{\mathcal{R}{1}} p\left(\mathbf{x} \mid \omega{2}\right) d \mathbf{x}\right]}{=0 \text { for minimax solution }} . \end{aligned}$$ 在后面那部分为0的时候, 极小化极大风险为: $$\begin{aligned} R{m m} &=\lambda_{22}+\left(\lambda_{12}-\lambda_{22}\right) \int_{\mathcal{R}{1}} p\left(\mathbf{x} \mid \omega{2}\right) d \mathbf{x} \\ &=\lambda_{11}+\left(\lambda_{21}-\lambda_{11}\right) \int_{\mathcal{R}{2}} p\left(\mathbf{x} \mid \omega{1}\right) d \mathbf{x} \end{aligned}$$

有时候我们需要在某个约束条件下最小化总风险, 比如我们做某个决策的资源是一定的, 就有约束:$$\int R\left(\alpha_{i} \mid \mathbf{x}\right) d \mathbf{x}<\text { constant for some particular } i .$$ 在这个情况下的贝叶斯决策需要满足Neyman-Pearson准则, 我们通常用多次调节决策边界的方法来达到目的.