Johnson Lindenstrauss Lemma - Publish Version

Last updated Dec 3, 2021 Edit Source

• All
• Machine learning
• Math

Tags: #MachineLearning #Math

• 对于高维数据，我们能够在降维的过程中保留其大部分的几何特征，即使降维的幅度非常大。

这是徐亦达老师让我们学习的第一个主题

¹

• MIT 6.854 Spring 2016 Lecture 5: Johnson Lindenstrauss Lemma and Extensions PDF(zotero://select/items/@mcnally2021RethinkingKeypoint)

  • MIT 6.854 Spring 2016 Lecture 5: Johnson Lindenstrauss Lemma and Extensions - YouTube
  • Course Website: 6.854/18.415 Advanced Algorithms, Spring 2016

• Course notes on dimensionality reduction from TTI and UBC

  • UBC Course homepage PDF(zotero://select/items/@prof.nickharvey2011UBCCPSC) This is the most Clear Version to me
  • TTI Course homepage - CMSC 3590 - Large Scale Learning, Spring 2009PDF(zotero://select/items/@shamkakade2009TTICMSC)

• Wikipedia:

  • Johnson–Lindenstrauss lemma - Wikipedia
  • 约翰逊-林登斯特劳斯定理 - 维基百科，自由的百科全书

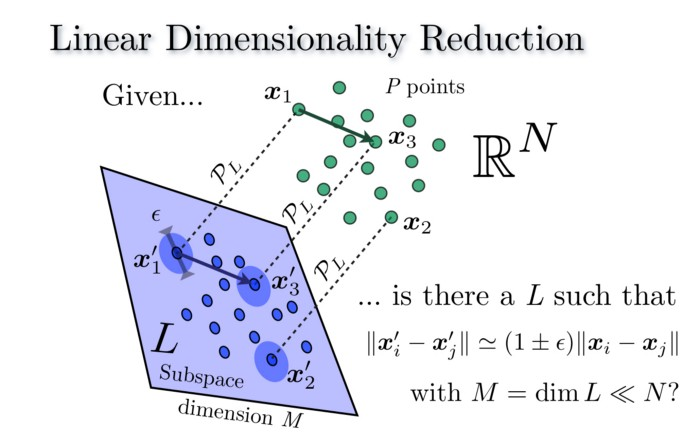
• $x_{1}, \cdots, x_{m} \in \mathbb{R}^{n}$ 是$n$维空间里面的任意$m$个点, $\epsilon\in(0,1)$.

• 则存在 $d$ 维空间里面的$m$个点 $y_{1}, \ldots, y_{m} \in \mathbb{R}^{d}$, 其中 $d=O\left(\log (m) / \epsilon^{2}\right)$ , 使得: $$ \begin{array}{rcl} (1-\epsilon)\left|x_{j}\right| \leq& \left|y_{j}\right| &\leq (1+\epsilon)\left|x_{j}\right| \qquad \forall j \\ (1-\epsilon)\left|x_{j}-x_{j^{\prime}}\right| \leq& \left|y_{j}-y_{j^{\prime}}\right| &\leq (1+\epsilon)\left|x_{j}-x_{j^{\prime}}\right| \qquad \forall j, j^{\prime} . \end{array} $$

• 并且我们能在多项式时间里面找到一个 $y_{j}:=L\left(x_{j}\right)$ 的线性变换 $L: \mathbb{R}^{n} \rightarrow \mathbb{R}^{d}$ 使得不等式成立的概率至少为 $1-2 / \mathrm{m} .$

• 后面我们可以看到这个线性变换可以是一个由许多正态分布的随机变量构成的随机矩阵$A \in \mathbb{R}^{k \times d}$.

• 这个引理可以从降维的角度来加速算法

  • 举个例子, 比如求最小生成树的Kruskal算法, 如果我们需要计算$H$维空间里面$n$个点最小生成树, 那么需要计算$C_n^2=O(n^2)$个距离, 每个距离的计算花费$O(H)$的时间($H$较大时), 那么总的时间复杂度是$O(n^2H)$
  • 根据JL引理, 我们可以降维的过程中保留其大部分的几何特征, 在降到$d$维后Kruskal算法的时间复杂度为:
    • 每一个降维的体现为一次矩阵运算$A_{d\times H}\vec v_{H\times 1}$, 时间复杂度为$O(dH)$, $n$个点总的时间复杂度为$O(dHn)$
    • 每一个距离的计算花费$O(d)=O\left(\log (m) / \epsilon^{2}\right)$, 总的距离计算需要花费$O\left(n^2d\right)$的时间.
    • 综上,总的时间复杂度为$O(dHn+n^2d)$, 在$d«H$的时候, 这个提升是很大的.

• 即使下面证明使用的是线性变换, JL引理同样适用于非线性变换. JL Lemma is tight.

• JL的证明是构造性(Constructive)的, 从证明里面可以看到, 虽然转换矩阵是一个随机矩阵, 但是求得这个矩阵的概率是很高的, 多试几次总会得到一个合适的矩阵.

• When to use the Johnson-Lindenstrauss lemma over SVD? - Theoretical Computer Science Stack Exchange

• The JL Lemma says essentially “you give me the error you want, and I’ll give you a low dimensional space that captures the distances upto that error”. It’s also a worst-case pairwise guarantee: for each pair of points, etc etc
• The SVD essentially promises “you tell me what dimension you want to live in, and I’ll give you the best possible embedding”, where “best” is defined as on average: the total error of true similarity versus projected similarity is minimum.

证明的思路如下图所示:

• 我们先如下构造一个线性变换$f: \mathbb{R}^{n} \rightarrow \mathbb{R}^{d}$

  • 构造$d$个$n$维的随机向量$r_i$, 每一个向量都由$n$个独立同分布的元素 $r_{i,j}$ 构成. 则$f$是下面这个矩阵 $F$ , 它将$n$维向量映射为$d$维向量: $$ F=\left[ \begin{array}{c} —r_{1}— \\ \vdots \\ —r_{d}—\\ \end{array} \right]_{d\times n} $$

• 对于$n$维单位向量 $v \in \mathbb{R}^{n}$ , $|v|=1$ 和 $d=O\left(\log (m) / \epsilon^{2}\right)$, 我们可以证明以下结论:

$$\operatorname{Pr}\left[1-\epsilon \leq \frac{|f(v)|}{\sqrt{d}} \leq 1+\epsilon\right] \geq 1-2 / m^{3} .$$

• 前面引理里提到的线性变换即$L(v):=f(v) / \sqrt{d}$, 因为$f$是线性的, 所以$L$也是线性的.

• 因为线性变换有这个优良的性质: $f(ax)=af(x)$, 所以上式其实可以推出任意向量$l_2$Norm的不变性: 对于任意长度的 $v$, 有$\frac v {|v|}$为单位向量, 带入上面的不等式: $$\operatorname{Pr}[(1-\epsilon)\leq|L(\frac v {|v|})| \leq(1+\epsilon)] \geq 1-2 / m^{3}$$ $$\Rightarrow$$ $$\operatorname{Pr}[(1-\epsilon)|v| \leq|L(v)| \leq(1+\epsilon)|v|] \geq 1-2 / m^{3}$$

如果我们将结果应用到 $v=x_{j}$ 和任意的 $v=x_{j}-x_{j^{\prime}}$ (对于 $j \neq j^{\prime}$ ). 因为一共有$(^m_2)=O(m^{2})$ 对向量, 所以进一步应用 union bound 可以得到: 任意一对向量不满足上面式子的概率最大为 $2 / \mathrm{m}$, 也就是成功的的概率为$1-2 / \mathrm{m}$.

Union_Bound-布尔不等式-Boole’s_inequality

For any events $A_{1}, A_{2}, \ldots, A_{n}$, we have $$ P\left(\bigcup_{i=1}^{n} A_{i}\right) \leq \sum_{i=1}^{n} P\left(A_{i}\right) $$

展开就是:

$$ \mathbb{P}\left(A_{1} \bigcup A_{2} \bigcup \cdots\right) \leq \mathbb{P}\left(A_{1}\right)+\mathbb{P}\left(A_{2}\right)+\cdots $$

• 这部分这个TTI的讲义讲的比较好(zotero://select/items/@shamkakade2009TTICMSC)

注意现在有 $O\left(m^{2}\right)$ 对向量 $u, v .$ 根据 union bound, $$ \begin{aligned} & \operatorname{Pr}\left(\exists u, v \text { s.t. the following event fails: }(1-\epsilon)|u-v| \leq|L(u-v)| \leq(1+\epsilon)|u-v|\right) \\ \leq & \sum_{\forall u, v} \operatorname{Pr}\left(\text { s.t. the following event fails: }(1-\epsilon)|u-v| \leq|L(u-v)| \leq(1+\epsilon)|u-v|\right) \\ \leq & \space m^2\times\frac 2 {m^3} \\ =& \frac 2 {m} \end{aligned} $$ 所以总的成功概率为$1-2 / \mathrm{m}$.

正态分布_高斯分布_Normal_Distribution-Gaussian_Distribution

• 我们可以把这个性质进一步推广到$m$个独立的随机变量: $Y_{1}, \ldots, Y_{m}$ 且 $Y_{i}$ 服从 $N(0,1)$. 对于标量 $\sigma_{1}, \ldots, \sigma_{m}$, 有 $\sum_{i} \sigma_{i} Y_{i}$ 服从 $N\left(0, \sum_{i} \sigma_{i}^{2}\right)$.

Chi-Squared_Distribution-卡方分布

正态独立随机变量的平方和是卡方分布的:

$$Y=Z_{1}^{2}+Z_{2}^{2}+\cdots+Z_{n}^{2}$$ then $Y$ is said to have a chi-squared distribution with $n$ degrees of freedom shown by $$Y \sim \chi^{2}(n)$$

$$\operatorname{Pr}\left[1-\epsilon \leq \frac{|f(v)|}{\sqrt{d}} \leq 1+\epsilon\right] \geq 1-\frac2 {m^{3}}$$

这个结论实际上是对称的, 我们只证明一半, 即只证明右边那半边的失败概率小于 $1/m^3$ :

$$\operatorname{Pr}\left[\frac{|f(v)|}{\sqrt{d}}\geq 1+\epsilon\right] \leq \frac1 {m^{3}}$$

为了方便, 我们可以平方一下里面的部分:

$$\operatorname{Pr}\left[|f(v)|^{2}>(1+\epsilon)^2 d\right]\leq1/m^3$$

• 证明的第一步是证明 $|f(v)|^{2}$ 实际上服从自由度为 $d$ 的卡方分布:

$$|f(v)|^{2}=|Fv|^2=\sum_{i=1}^{d}\left(r_{i}^{T} v\right)^{2}$$

其中 $r_{i}^{T} v$ 是第 $i$ 行与向量 $v$ 的点乘, 即转化后的向量$f(v)$里面的第$i$个元素. 我们令其为 $X_i$, 容易知道 $X_i$ 是 $n$ 个服从标准正态分布的随机变量 $r_i$ 的加权和: $v_1r_{i1}+v_2r_{i2}+\cdots+v_nr_{in}$, 权值是 $v$ 的对应元素, 所以 $X_i\sim N\left(0, \sum_{i} v_{i}^{2}\right)=N(0,1)$. (因为 $\sum_{i} v_{i}^{2}=|v|=1$)

所以上面的式子可以表示为:$$|f(v)|^{2}=\sum_{i=1}^{d} X_{i}^{2}$$

容易见得$|f(v)|^{2}\sim \chi^{2}(d)$, $d$是自由度.

• 证明的第二步是利用类似于Chernoff Bound的方法来对事件 ( $|f(v)|^{2}>(1+\epsilon)^2 d$ ) 发生的概率上限进行约束:

我们先简化一下问题的表述:

令 $Y=|f(v)|^2=\sum_{i=1}^{d} X_{i}^{2}$ , 令 $\alpha=d(1+\epsilon)^{2}$. 需要证明的命题可以表述为:$$\operatorname{Pr}[Y>\alpha] \leq \frac1 {m^{3}} \tag{1}$$

我们下面将证明

$$\operatorname{Pr}[Y>\alpha] \leq \exp \left(-(3 / 4) d \epsilon^{2}\right)\tag{2}$$

在 $d=4 \ln (m) / \epsilon^{2}$ 的时候, $(1)$与$(2)$等价: $$\begin{aligned}\exp(\frac{-3} 4 d \epsilon^{2}) &=\exp(\frac{-3}4 \epsilon^{2}\frac{4\ln(m)}{\epsilon^{2}})\\ &=\exp(-3\ln(m))\\ &=\exp(\ln(m^{-3}))\\ &=\frac1 {m^{3}} \end{aligned}$$

令 $t\in [0,1/2)$, 像 Chernoff Bounds里面一样, 我们可以把不等式换到指数部分里面去, 然后再应用Markov不等式:

$$\operatorname{Pr}[Y>\alpha]=\operatorname{Pr}\left[e^{t Y}>e^{t \alpha}\right] \leq \frac {\mathrm{E}\left[e^{t Y}\right]}{e^{t \alpha}}\tag{3}$$

随后, 因为$Y=\sum_{i=1}^{d} X_{i}^{2}$, 而 $X_i$ 是相互独立的, 所以求和符号可以换到求数学期望的外面去:

$$\mathrm{E}\left[e^{t Y}\right]=\mathrm{E}\left[\exp \left(t \sum_{i=1}^{d} X_{i}^{2}\right)\right]=\prod_{i=1}^{d} \mathrm{E}\left[\exp \left(t X_{i}^{2}\right)\right]\tag{4}$$

对于$\mathrm{E}\left[\exp \left(t X_{i}^{2}\right)\right]$, 结合 关于随机变量函数的期望, 我们可以将这个期望按照定义展开:

$$\mathrm{E}(g(X))=\int_{\Omega} g(x) f(x) \mathrm{d} x$$ $$\Rightarrow$$ $$\begin{aligned} \mathrm{E}\left[\exp \left(t X_{i}^{2}\right)\right] &= \int_{-\infty}^{\infty} \exp \left(t y^{2}\right) f(y) d y\qquad (其中f(y)是X的概率密度函数)\\ &=\int_{-\infty}^{\infty} \exp \left(t y^{2}\right) \frac{1}{\sqrt{2 \pi}} \exp \left(-y^{2} / 2\right) d y\\ &=\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{\infty} \exp \left(t y^{2}\right) \exp \left(-y^{2} / 2\right) d y\\ &=\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{\infty} \exp \left(-y^{2}\left(\frac{1}{2}-t\right)\right) d y\end{aligned}$$

观察上面的式子, 如果 $t=0$, 那么这个式子就是一个标准正态分布的概率密度函数在整个数轴上面的积分, 结果为$1$. 为了达到相似的效果, 我们可以通过换元得到一个类似的形式:

令$z=y \sqrt{1-2 t}$, 有:

$$\begin{aligned} \mathrm{E}\left[\exp \left(t X_{i}^{2}\right)\right] &=\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{\infty} \exp \left(\frac{-(y \sqrt{1-2 t})^{2}}2\right) d y \\ &=\frac{1}{\sqrt{2 \pi} \sqrt{1-2 t}} \int_{-\infty}^{\infty} \exp \left(-z^{2} / 2\right) d z \\ &=\frac{1}{\sqrt{1-2 t}} \end{aligned}$$

结合$(3), (4)$, 可以得到: $$\begin{aligned} \mathrm{E}\left[e^{t Y}\right]&= \prod_{i=1}^{d}\mathrm{E}\left[\exp\left(tX_i^{2}\right) \right]\\ &=(1-2 t)^{-d / 2} \end{aligned}$$ $$\operatorname{Pr}[Y>\alpha] \leq \frac {(1-2 t)^{-d / 2}}{e^{t \alpha}}=e^{-t \alpha}(1-2 t)^{-d / 2}$$

接下来我们只需要选择一个合适的 $t$ 即可, 我们令 $t=(1-d / \alpha) / 2$

$$\operatorname{Pr}[Y>\alpha] \leq e^{-t \alpha}(1-2 t)^{-d / 2}=e^{(d-\alpha) / 2}(d / \alpha)^{-d / 2}$$

现在我们带入$\alpha=d(1+\epsilon)^{2}$, 得到: $$\exp \left(\frac{d}{2}\left(1-(1+\epsilon)^{2}\right)-\frac{d}{2} \ln \left(\frac{1}{(1+\epsilon)^{2}}\right)\right) =\exp \left(-d\left(\epsilon+\epsilon^{2} / 2-\ln (1+\epsilon)\right)\right)$$

%%注意括号里面的这部分: $\epsilon+\epsilon^{2} / 2-\ln (1+\epsilon)$%%

我们的证明目标是 $-(3 / 4) d \epsilon^{2}=-d\frac3 4\epsilon^{2}$, 所以我们只需要证明: $$\begin{aligned} -d\left(\epsilon+\epsilon^{2} / 2-\ln (1+\epsilon)\right)&\leq-d\frac3 4\epsilon^{2}\\ \epsilon+\epsilon^{2} / 2-\ln (1+\epsilon)&\geq\frac3 4\epsilon^{2}\\ (\epsilon+\epsilon^{2} / 2)-\frac3 4\epsilon^{2}&\geq\ln (1+\epsilon)\\ \epsilon-\epsilon^{2} / 4&\geq\ln (1+\epsilon)\\ \end{aligned}$$ 即可

利用函数的凹凸性, 我们可以证明在$x \in[0,1]$有 $\ln (1+x) \leq x-x^{2} / 4$

两者在0取值都是0, 一阶导数都是1, 二阶导数$\ln (1+x)$是负的, $x-x^{2} / 4$是正的.

综上: $$\operatorname{Pr}[Y>\alpha] \leq \exp \left(-d\left(\epsilon+\epsilon^{2} / 2-\left(\epsilon-\epsilon^{2} / 4\right)\right)\right) \leq \exp \left(-(3 / 4) d \epsilon^{2}\right)$$

我们即证明了Norm Preservation Lemma, 从而证明了Johnson Lindenstrauss Lemma

有的证明, 比如 TTI (zotero://select/items/@shamkakade2009TTICMSC), MIT(zotero://select/items/@prof.ankurmoitra2016MIT854)讲义里面的证明, 都应用了Chi-Square Distribution的一个 Chernoff Bounds:

Lemma 4 (Chernoff bound for chi-square distributions). $$ \begin{aligned} &\mathbb{P}\left[\sum_{i=1}^{k} Y_{i}^{2}>(1+\epsilon) k\right] \leq e^{-\frac{k}{4}\left(\epsilon^{2}-\epsilon^{3}\right)} \\ &\mathbb{P}\left[\sum_{i=1}^{k} Y_{i}^{2}<(1-\epsilon) k\right] \leq e^{-\frac{k}{4}\left(\epsilon^{2}-\epsilon^{3}\right)} \end{aligned} $$ Now, we may set $k=O\left(\frac{\log (1 / \delta)}{\epsilon^{2}}\right)$ and get $|A x|{2}^{2} {\sim\over1\pm\epsilon}|x|{2}^{2}$ with probability at least $1-\delta$.

但是Chernoff Bound的证明很复杂, 我觉得UBC课件里面的证明(即上面的证明)更好.