Understanding Bayes' Theorem
# Understanding Bayes’ Theorem
Tags: #Math/Probability #Bayes
单从形式上来说, Bayes定理是十分简单的. 但是如果我们结合实际问题与一点几何直觉, Bayes定理可以从两个独特的角度来直观理解:
- Update of Prior Beliefs & Change of Perspective
# Bayes’ Theorem: Statement
$$P(A \mid B)=\frac{P(B \mid A) P(A)}{P(B)}$$
- 其中$P(A \mid B)$也称为A的后验概率(posterior probability of A given B), 因为我们已经知道了B.
- 而$P(A)$称为A的先验概率 (prior probability or marginal probability), 因为我们没有加任何条件.
Bayes定理还有不同的形式:
我们可以把$P(B)$拆开: $$P(A \mid B)=\frac{P(B \mid A) P(A)}{P(B \mid A) P(A)+P(B \mid \neg A) P(\neg A)}$$
从条件概率(Conditional Probability)的角度来理解, 分子也可以替换为$P(A\cap B)$: $$P(A \mid B)=\frac{P(A\cap B)}{P(B)}$$ 这其实就是条件概率的定义.
# Bayes’ Theorem: Counter-intuitive Side
这些科普视频都集中展现了Bayes定理的反直觉的一面:
- How To Update Your Beliefs Systematically - Bayes’ Theorem - YouTube
- Bayes theorem, the geometry of changing beliefs - YouTube
- The medical test paradox, and redesigning Bayes’ rule - YouTube
Bayes定理为什么在上面的例子里面会给出反直觉的结论?
因为即使误检率很低, 要是基数很大的话, 呈阳性的人里面也会有很大一部分是患病的人, 所以即使检出了阳性, 实际患病的概率还是很小的:
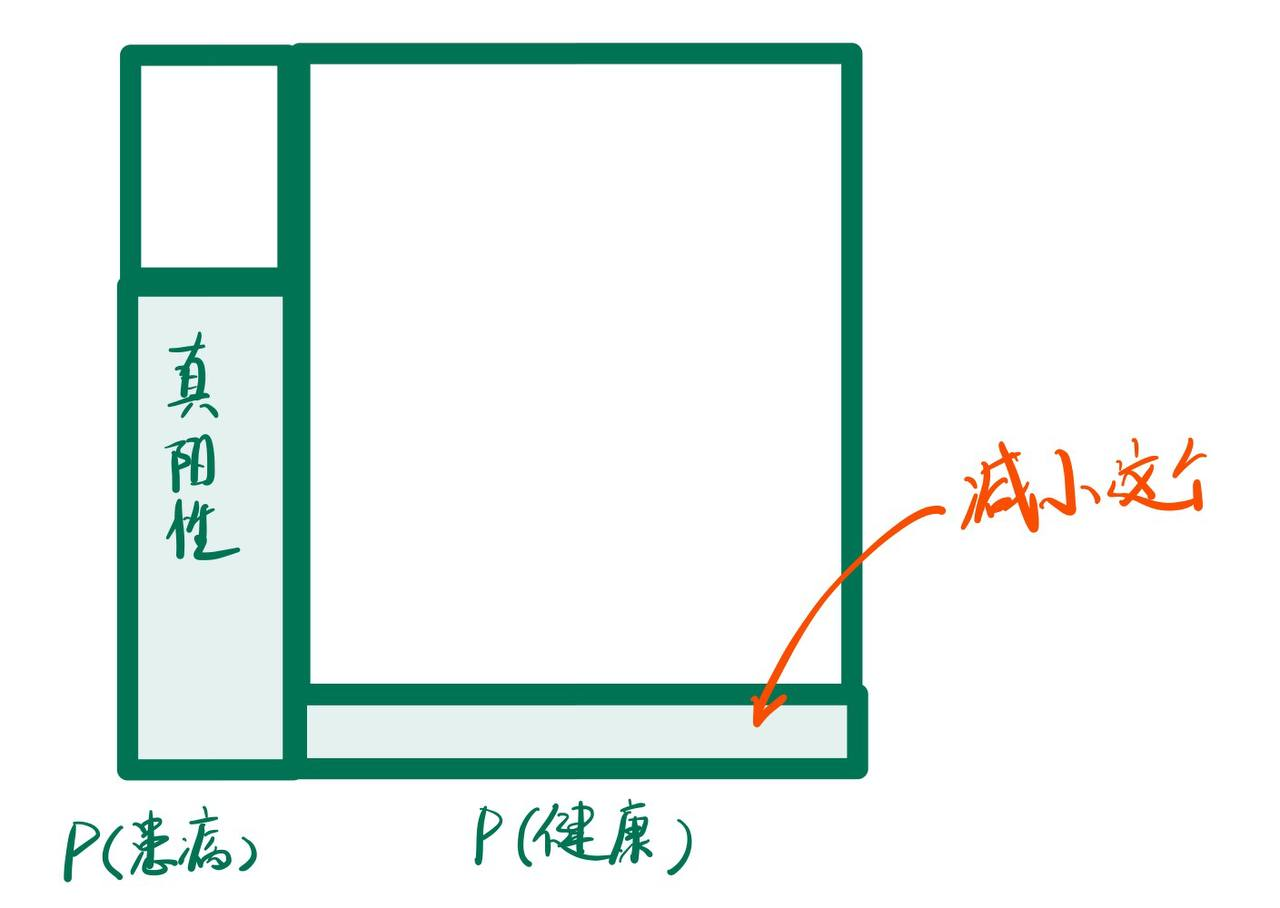
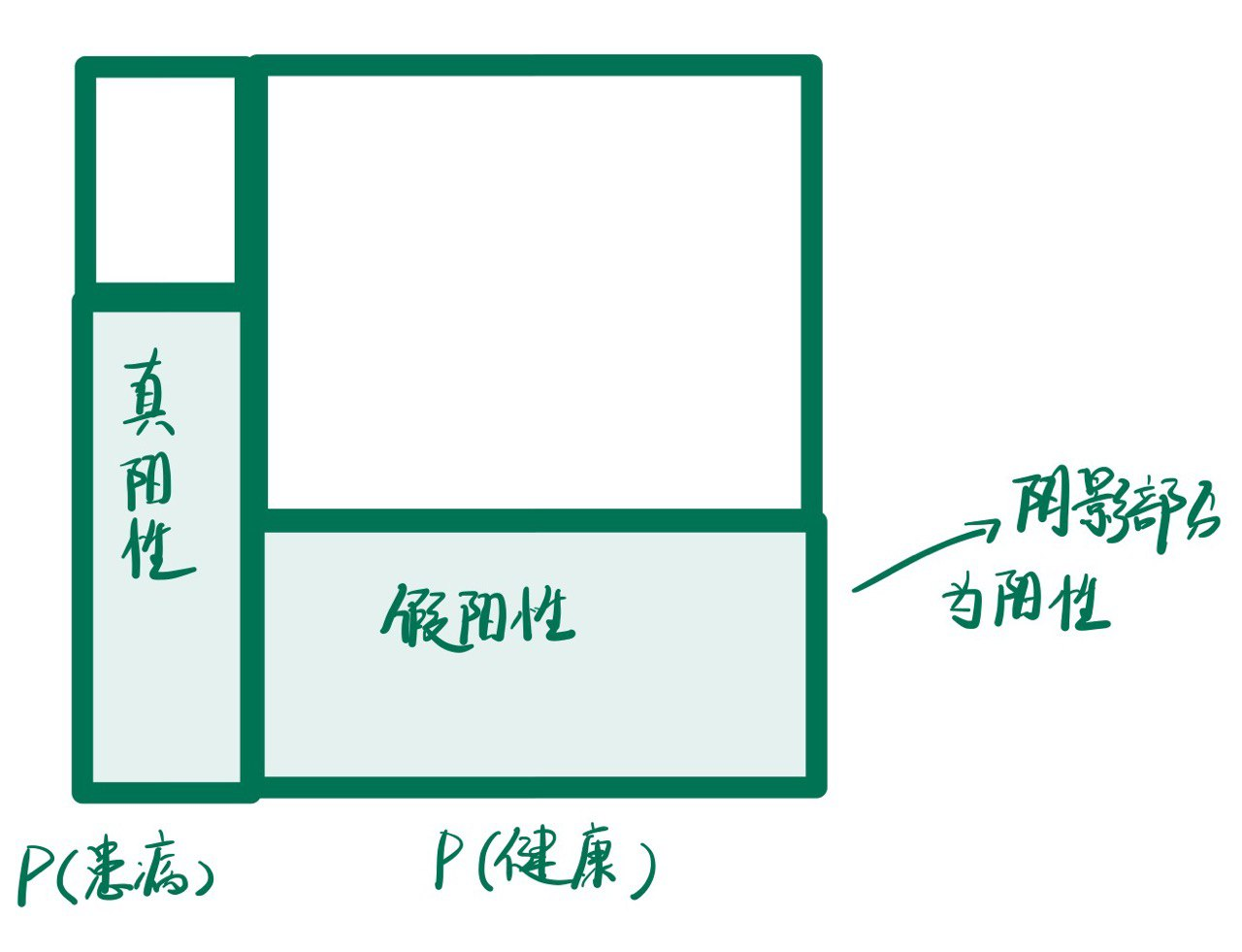 要想提高检出正确阳性的概率, 就应该减小"健康的人检出为阳性的概率(Specificity)"
要想提高检出正确阳性的概率, 就应该减小"健康的人检出为阳性的概率(Specificity)"
一个检测方法的正确率其实需要两个指标来衡量:
- 敏感度(Sensitivity): 对于患病者, 有多大概率检出ta为患病的(True Positive Rate)
- 明确度(Specificity): 对于健康的人, 有多大概率能正确得出ta为健康的(True Negative Rate)
# Bayes’ Theorem: Intuitive Geometry Representation
- 首先, 我们需要注意其实"条件概率的表示方法"让贝叶斯定理没有那么直观了:
# Geometry Representation:
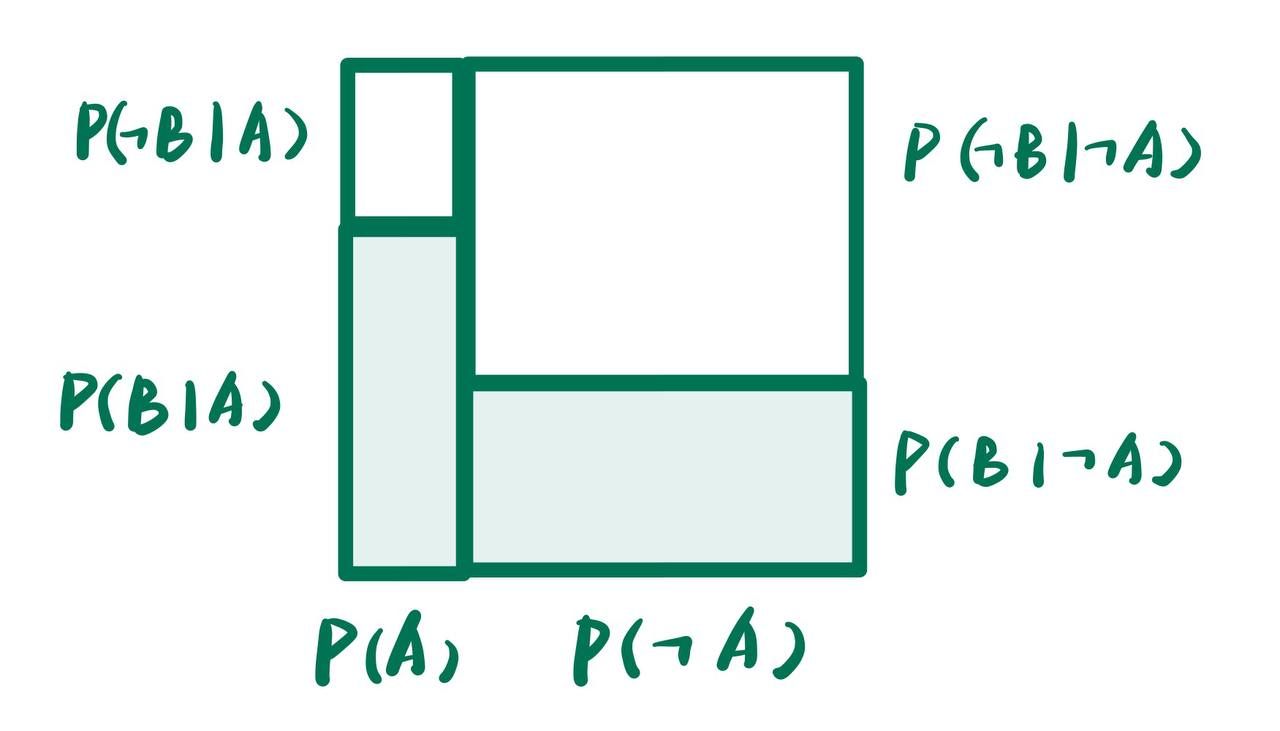
我们可以用上图来形象地说明贝叶斯定理的组成.
为了得到上图, 首先我们将A的概率分布$P(A)$和$P(\neg A)$表示到一个正方形里面:
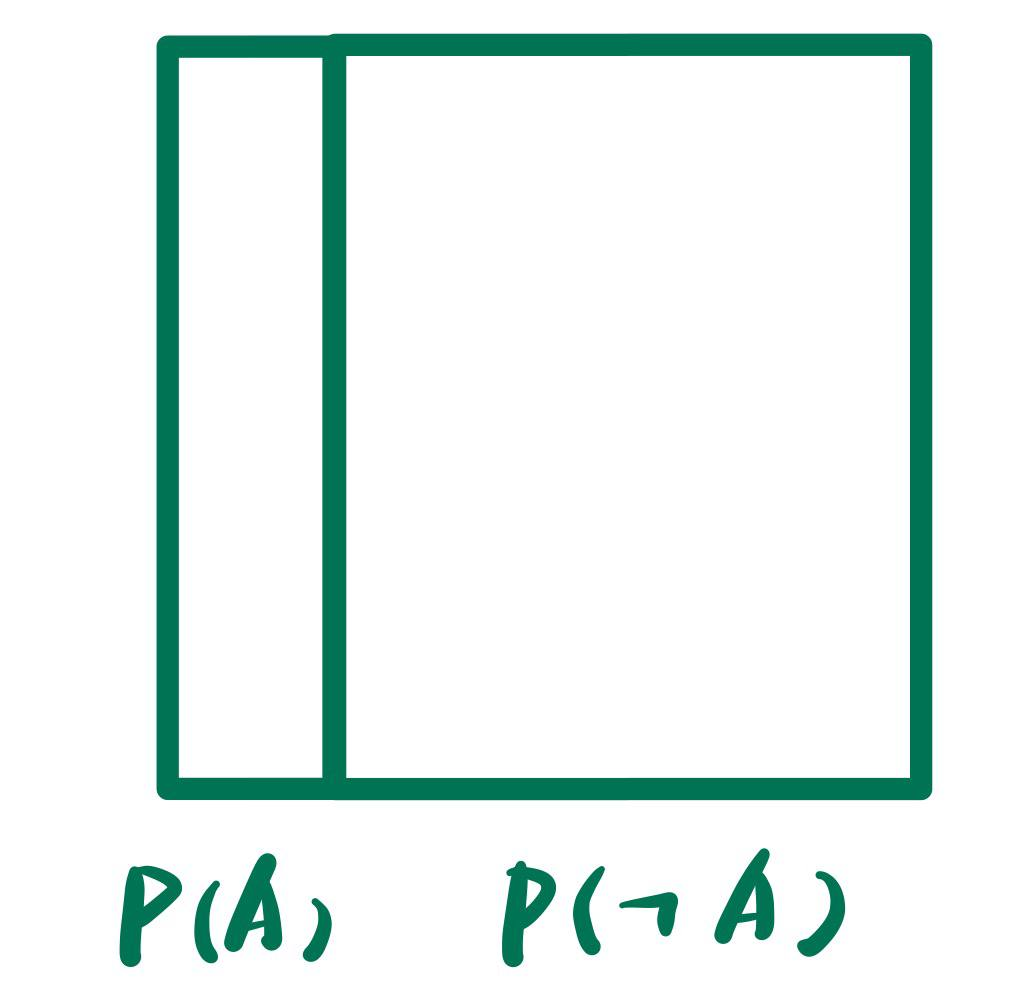 这个正方形边长为1, 满足$P(A)+P(\neg A)=1$
这个正方形边长为1, 满足$P(A)+P(\neg A)=1$同样, 对于事件B的概率分布, 我们也可以表示为一个正方形:
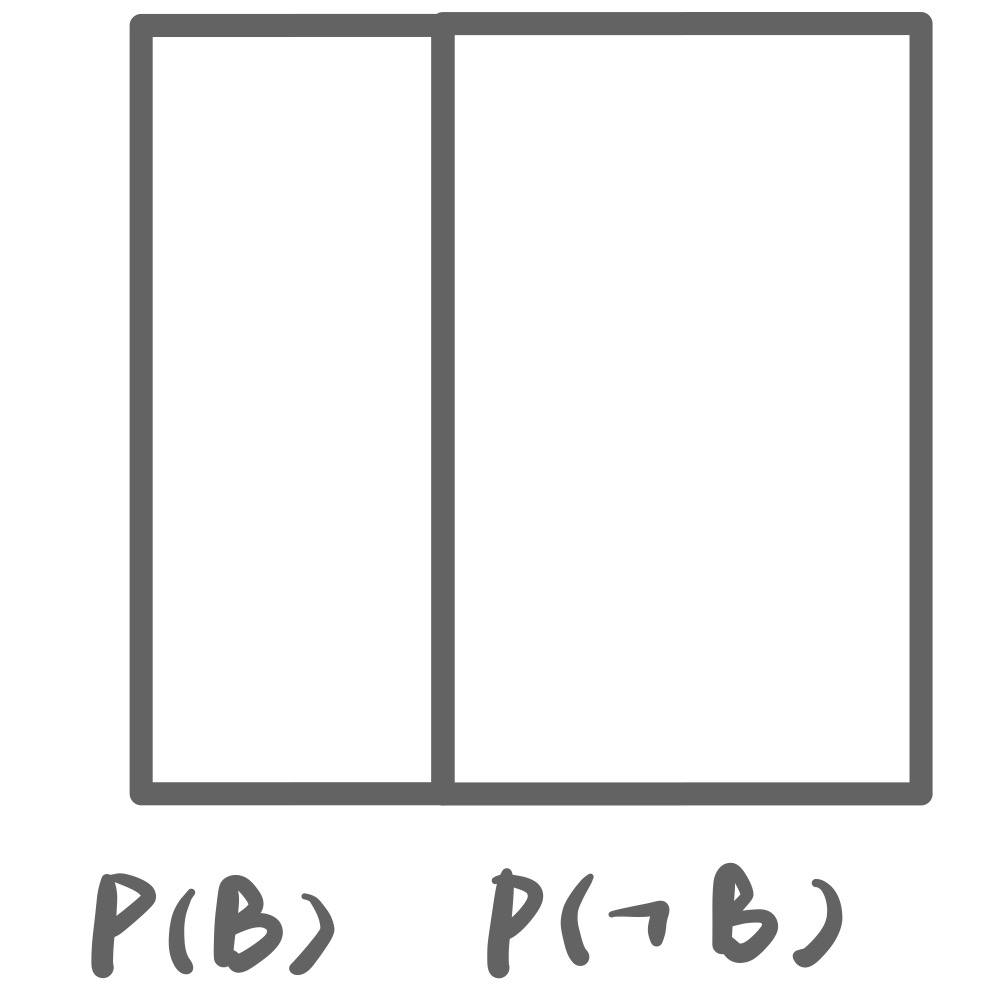
如果$A, B$是相互独立的, 那么它们的概率分布可以表示为:
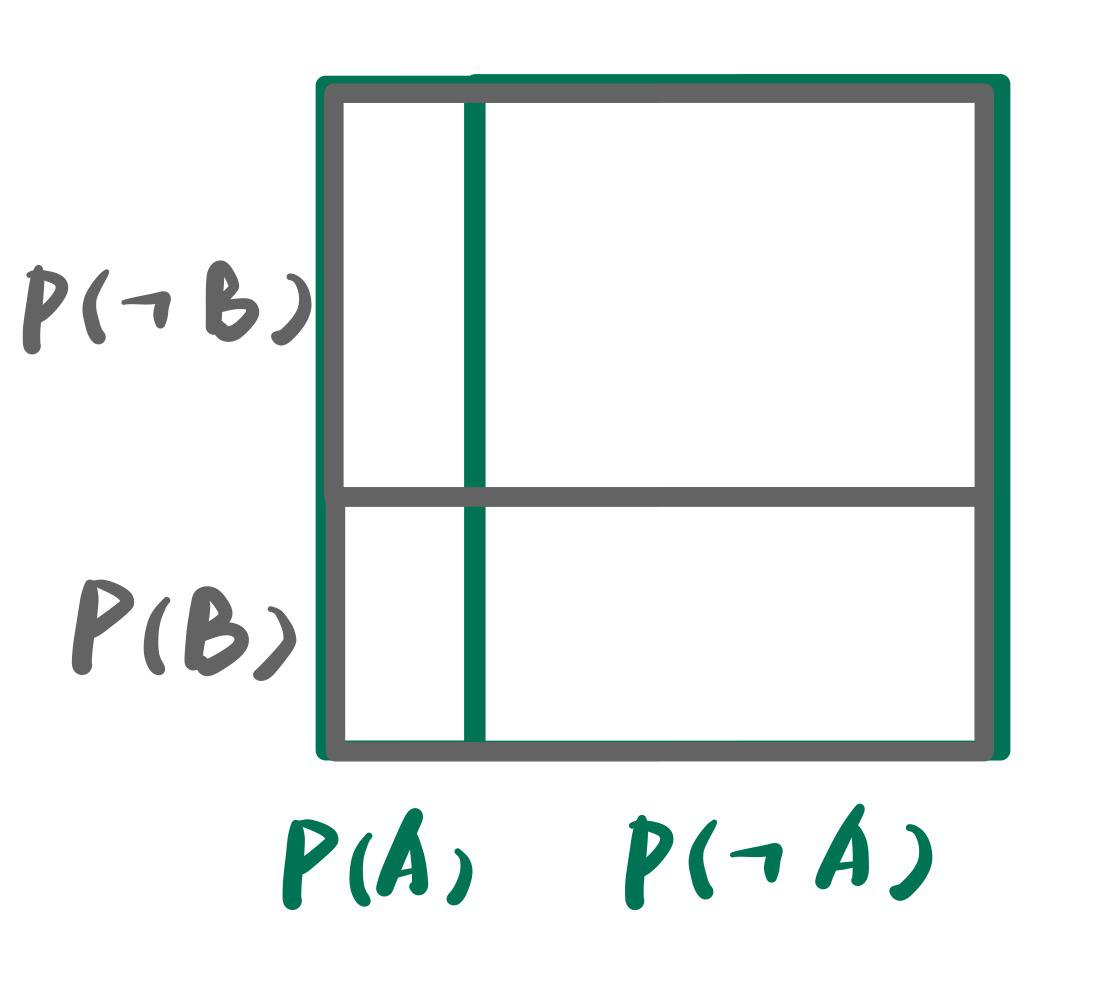 有$P(AB)=P(A)P(B)$
有$P(AB)=P(A)P(B)$但是如果$A,B$是相关的, 又该怎么表示它们的概率分布呢?
- 若$A,B$是相关的, 说明如果我们知道了$A$, 那么$B$的概率分布会因为$A$的取值的不同而不同:
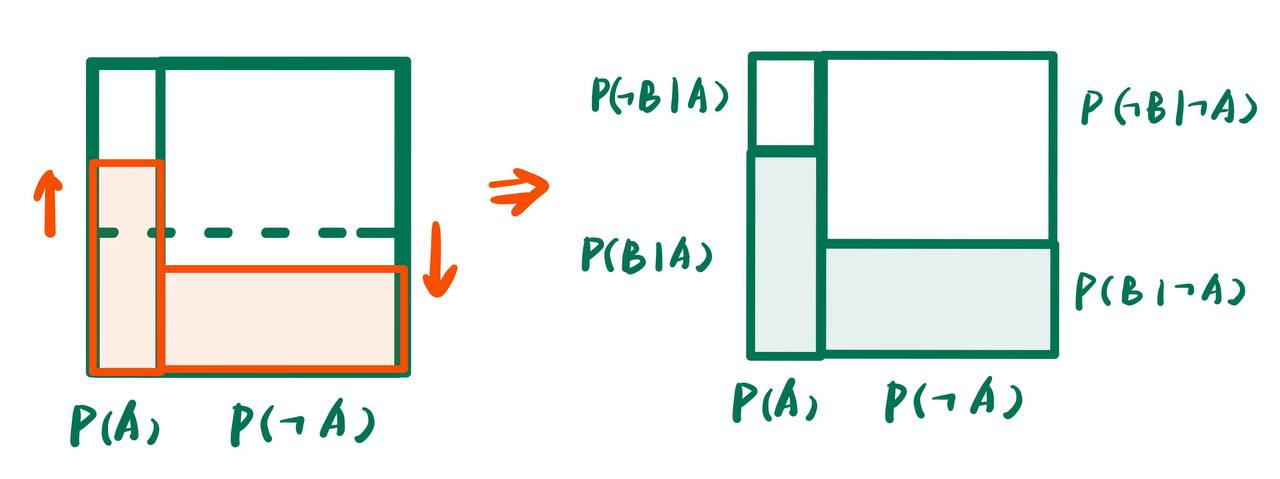
- 在上图中, $A=1$的时候, B的概率上升了, $A=0$的时候, B的概率下降了.
- 此时阴影部分的面积之和表示$P(B)=P(B\mid A)P(A)+P(B\mid\neg A)P(\neg A)$
- 注意B在左右的概率分布变化不一定要一个上升一个下降, 它们的变化是完全无关的. 它们可以都上升或者都下降:
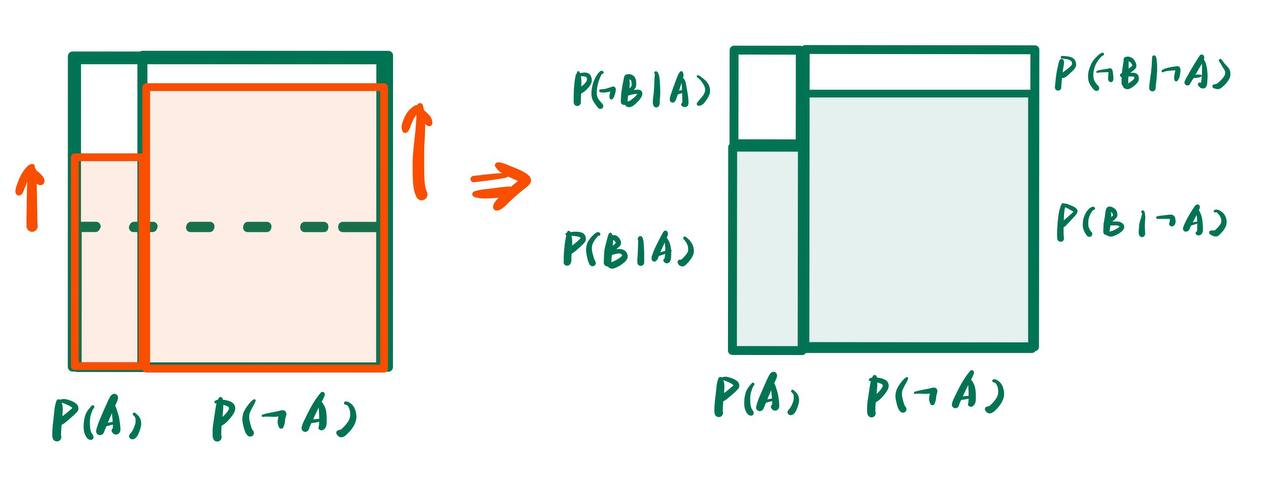 这样, 我们就用几何直观表达了两个相关变量的概率分布. 每一个小长方形都代表了一种AB的取值情况.
这样, 我们就用几何直观表达了两个相关变量的概率分布. 每一个小长方形都代表了一种AB的取值情况.
- 若$A,B$是相关的, 说明如果我们知道了$A$, 那么$B$的概率分布会因为$A$的取值的不同而不同:
那么, Bayes定理怎样从图形里面得到呢? 将小长方形与概率对应起来, 我们有:
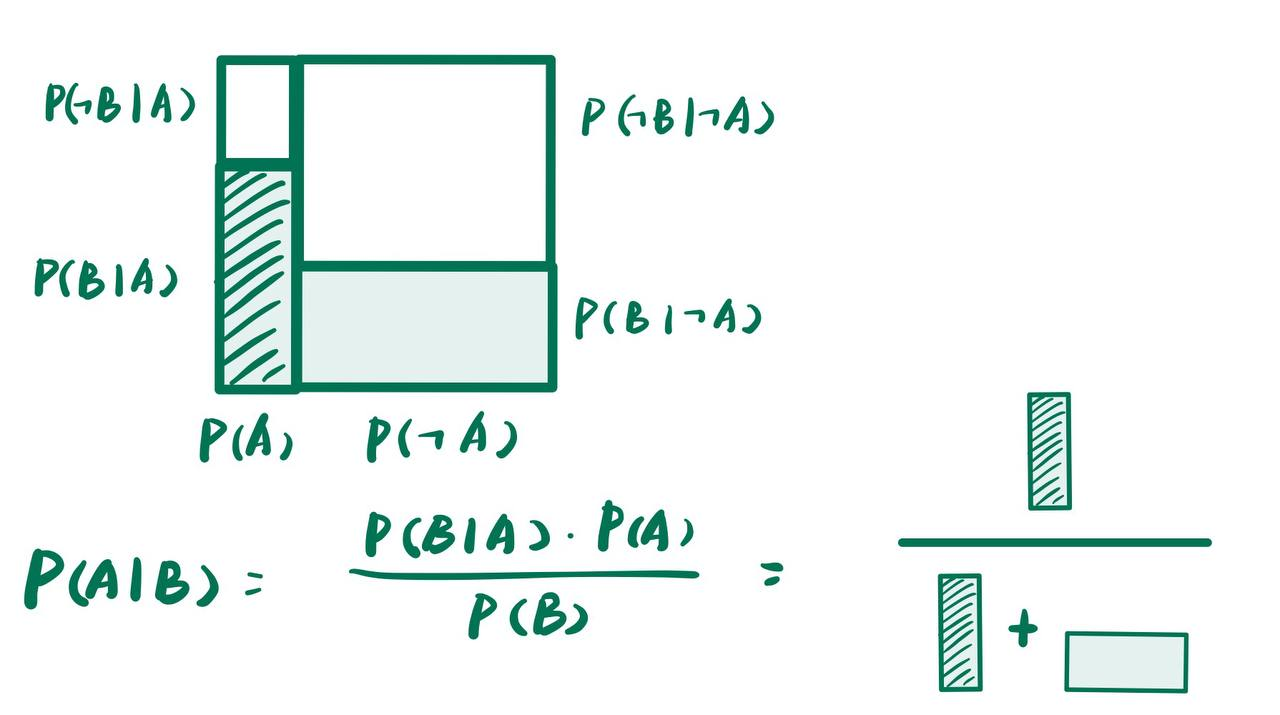
# Update of Prior Beliefs
- 现在我们能够用Update of Information的观点来看待Bayes定理了, 在上面的图像里面, 我们假设事件A代表患病, 事件B代表检测为阳性.
- 在我们还没有进行检测的时候, 我们对于患病的理解概率的理解是这样的;

- 但是现在进行了检测B, 意味着我们对于是否患病有了更多的信息. 当我们再次计算患病概率的时候, 我们应该更新之前的认识, 在新的图形上面计算患病的后验概率:

- 在我们还没有进行检测的时候, 我们对于患病的理解概率的理解是这样的;
下面这个视频片段也许解释的更清楚一点:
- 在日常生活中, 我们每天都在做大大小小的决定. 在大部分情况下, 我们都会综合权衡"过去的经验"和"当下的具体情况", 然后做出一个"最佳"的决定.
- 其实我们过去的"经验"就相当于先验概率$P(A)$, 而具体情况就是新出现的事件$B$. 综合权衡的过程就是在看这个新出现的事件B对于我们过去的经验产生了怎样的影响(求后验概率$P(A\mid B)$)
# Change of Perspective
下面这个观点是我自己探索出来的, 这个观点侧重于从个体角度上来理解Bayes定理:
首先我们需要介绍概率分布的第二个表示方法.
- 前面我们将$A, B$的概率分布表示为下图的形式:
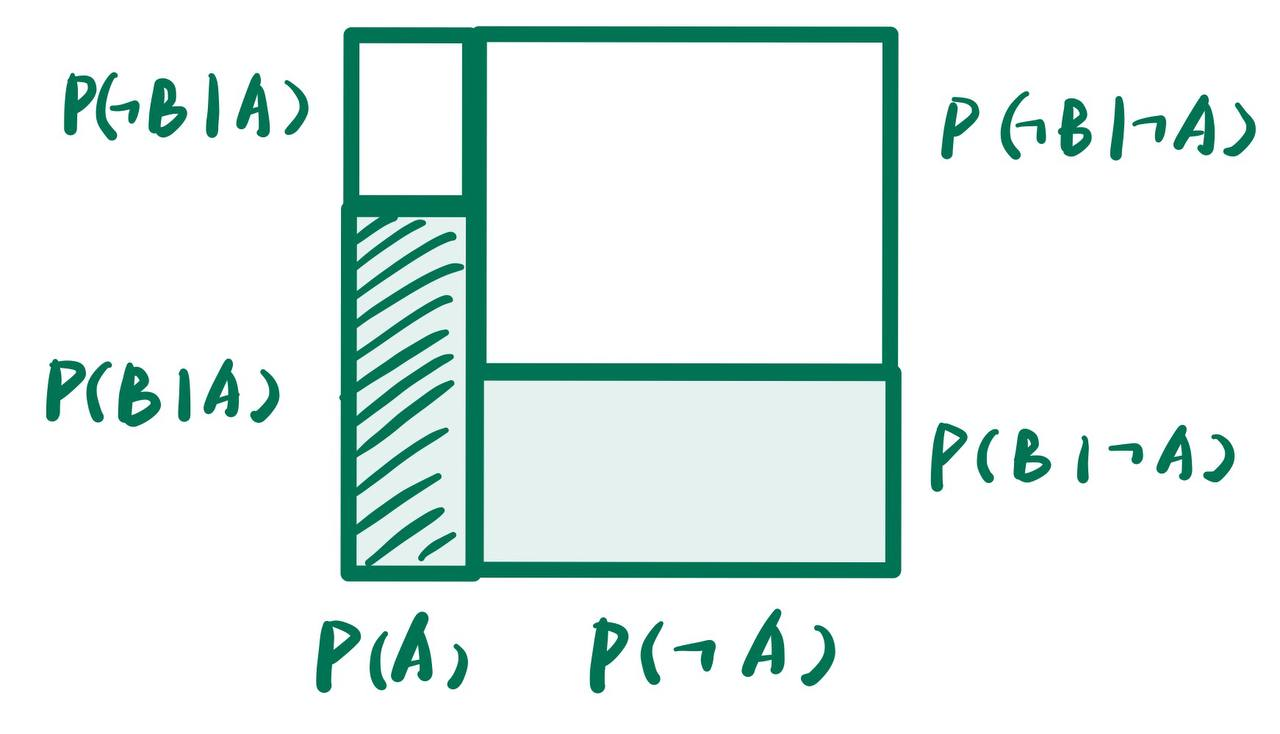 观察这个图, 我们可以看到A的概率分布表示很简单, 但是B的概率分布表示很复杂.
我们可以理解为我们先知道了A的概率分布, 然后再在此基础上添加了B(从下向上看):
观察这个图, 我们可以看到A的概率分布表示很简单, 但是B的概率分布表示很复杂.
我们可以理解为我们先知道了A的概率分布, 然后再在此基础上添加了B(从下向上看):
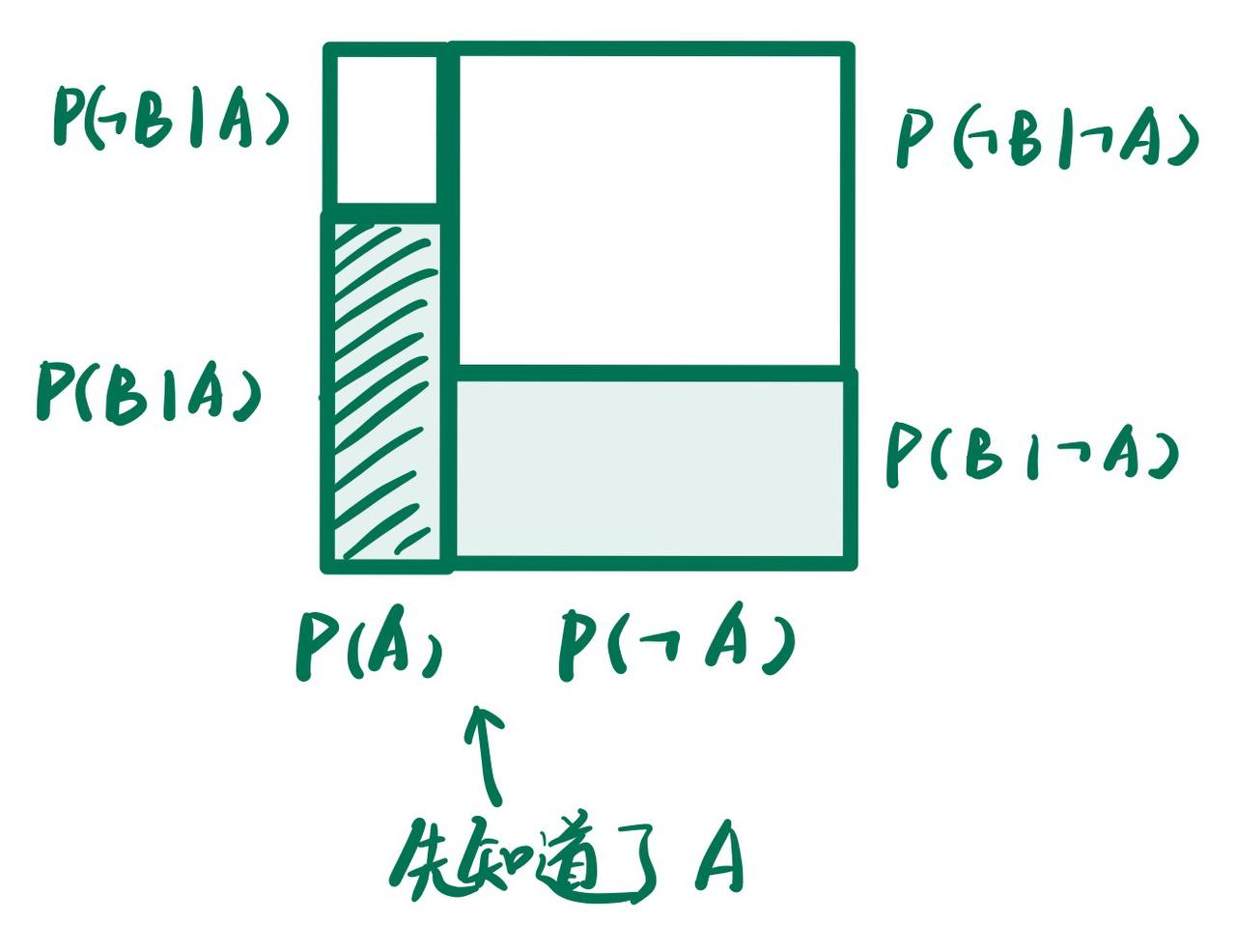
- 前面我们将$A, B$的概率分布表示为下图的形式:
这显然对于B是十分不公平的, 我们用可以类似的思路变化一下表示方法:
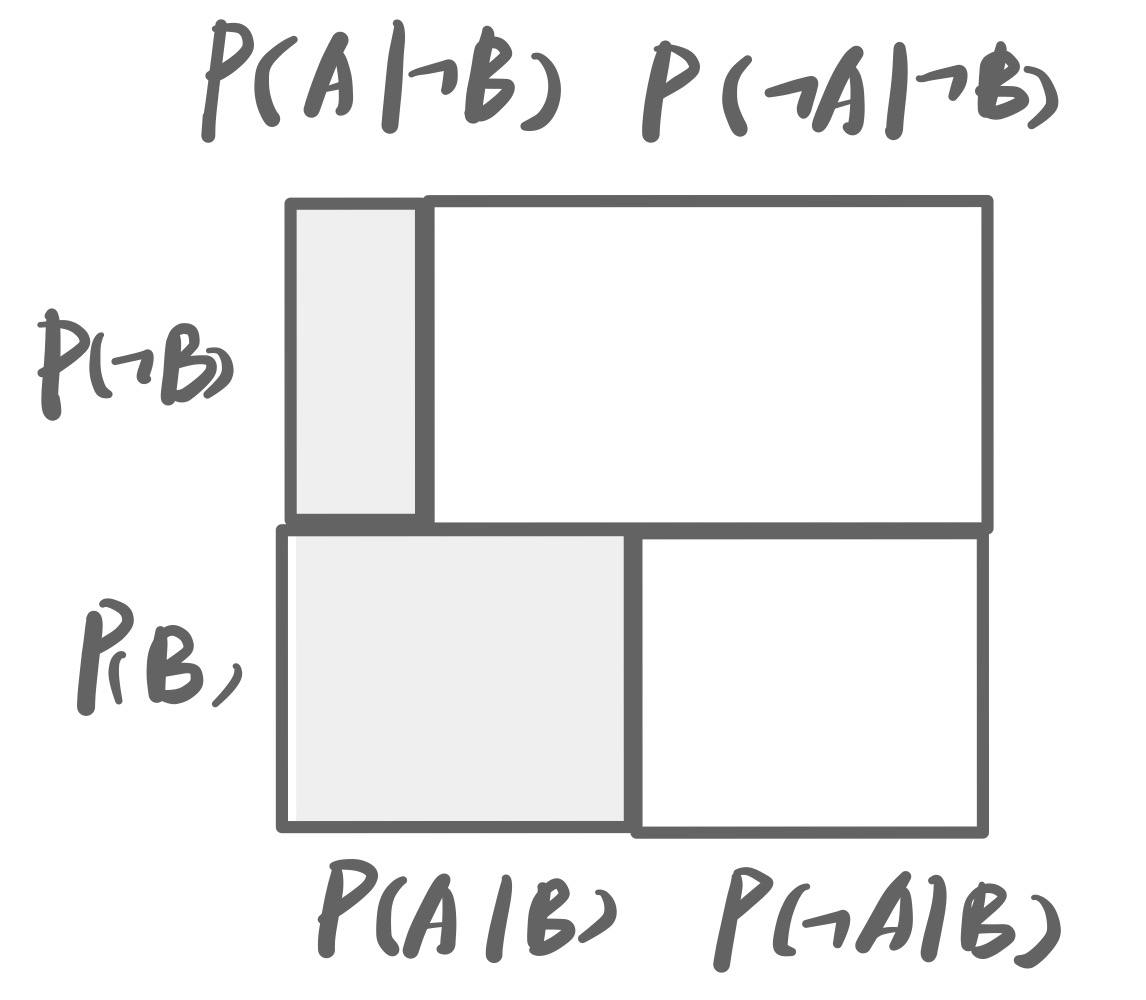 注意图像里面每个小长方形仍然对应不同情况下的概率, 只是形状变了, 面积没有变.
注意图像里面每个小长方形仍然对应不同情况下的概率, 只是形状变了, 面积没有变.- 我们可以理解为先确定了B, 然后再添加了A的概率分布:
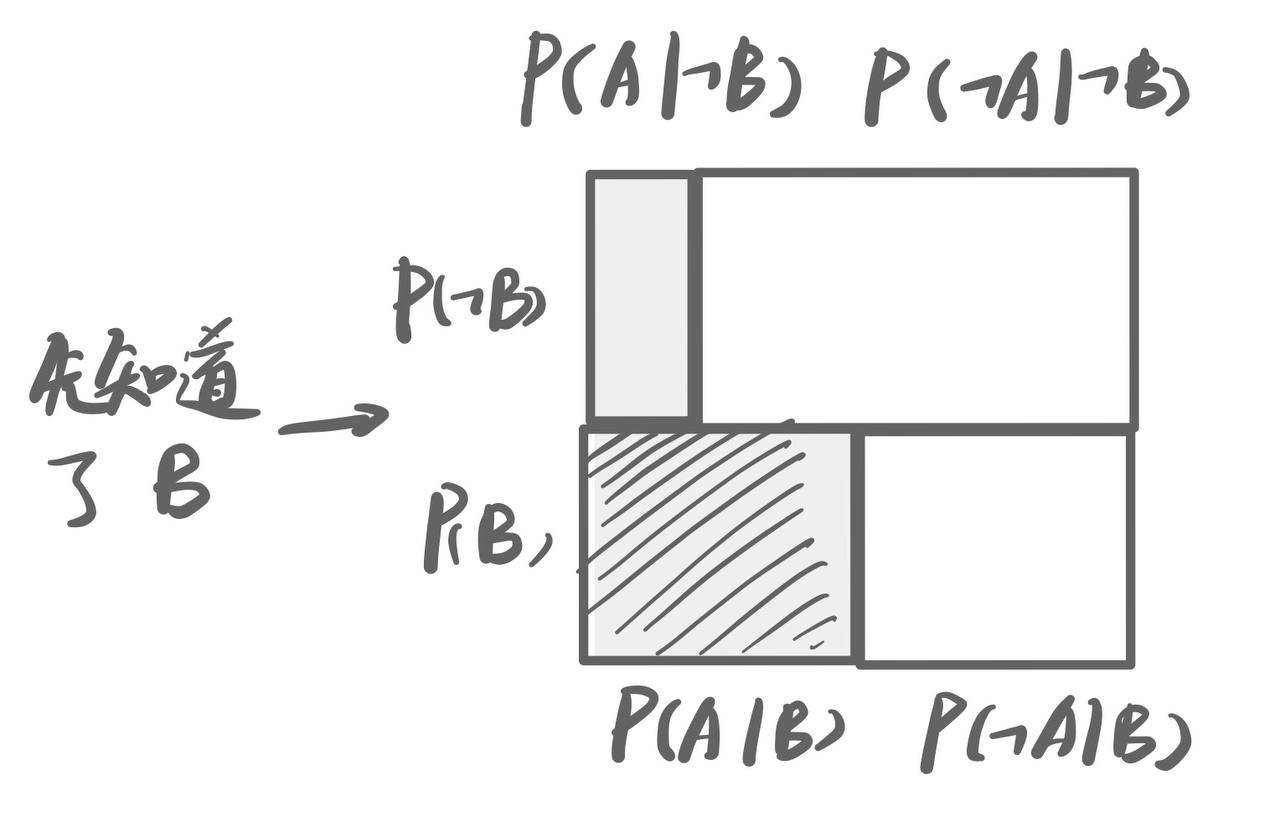
- 我们可以理解为先确定了B, 然后再添加了A的概率分布:
对比一下两个表示:
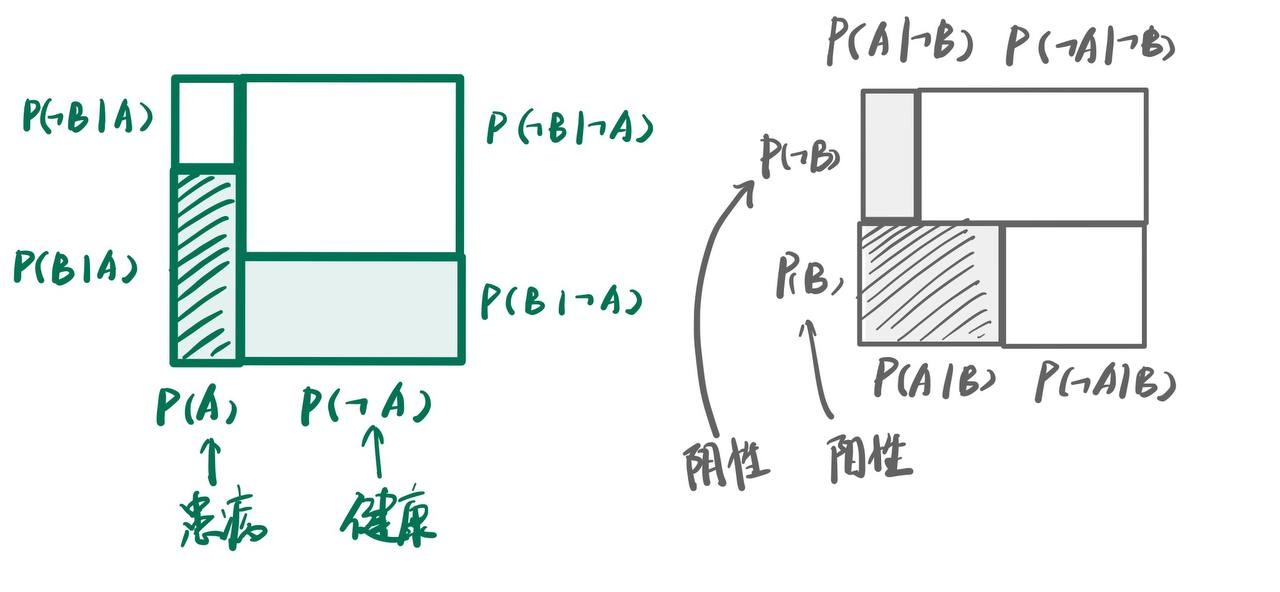
对于左边的图, 我们可以理解为一种"总体的角度". 即对于一大群人, 有患病的, 也有不患病的, 而后来加入的B的概率分布解释了这个检测方法对于不同情况的人群的效果.
对于右边的图, 我们这可以理解为一种"个体的角度", 即对于一个人, ta做了检测后要么为阳性要么为阴性, 没有其他情况, 而后来加入的A的分布给出了这个人不同检测结果的患病概率.
而Bayes’ Theorem就是在这两种视角之间转换的方式.
现在我们来观察Bayes的公式:
$$P(A \mid B)=\frac{P(B \mid A) P(A)}{P(B)}$$
如果你去做了癌症检查, 得到了阳性结果(事件B), 那么你一定很想知道你真的有癌症的概率有多大 (即概率$P(A\mid B)$ ). 用右边的图来理解, 即你已经确定B发生了, 可以只关注图片的下半部分:
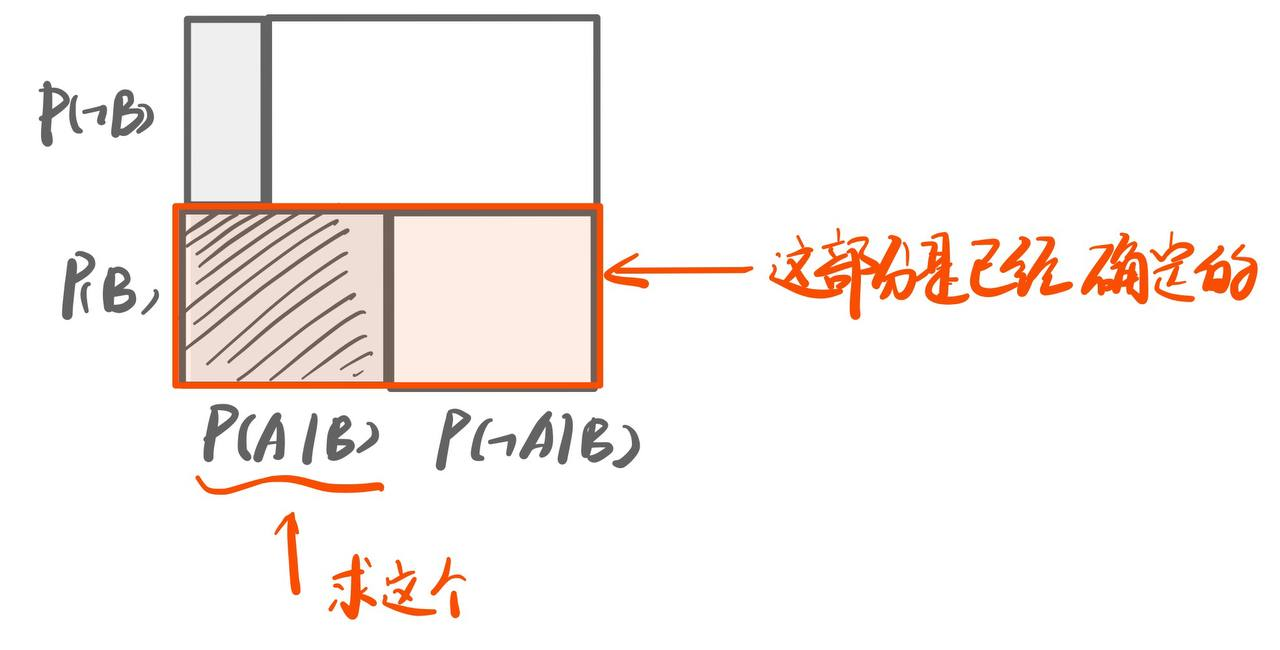
而我们常常这样计算$P(A\mid B)$: $$P(A \mid B)=\frac{P(B \mid A) P(A)}{P(B \mid A) P(A)+P(B \mid \neg A) P(\neg A)}$$ 其中$P(A), P(B \mid A), P(B \mid \neg A)$分别表示疾病的发生率, 检测方法的Sensitivity和Specificity, 计算时通常它们都是已知的或者可以使用频率近似代替概率.
- 用图形表示就是: (我们只需要关注阴影部分, 即已经确定的范围)

注意我们计算这个概率使用的是左边的图, 即"总体的角度", 而我们得到的结果是"个体的角度"里面的指标$P(A\mid B)$ : 一个已经检测为阳性的人的患病概率. 也就是说, Bayes定理实现了视角的切换(Change of Perspective)
- 注意总体角度和个人角度其实是可以交换的, 比如我们将左边的图看作个体角度, 则公式: $$P(B \mid A)=\frac{P(A \mid B) P(B)}{P(A)}$$ 可以理解为在一个人已经患病的情况下, ta检测得到阳性结果的概率(检测方法的Sensitivity).
# 拓展
有了直观的表示方法, Bayes定理可以很容易地推广到多个类的情况:
如果A有多个类: $$\begin{aligned} &P(B)=\sum_{j} P\left(B \mid A_{j}\right) P\left(A_{j}\right) \\ &\Rightarrow P\left(A_{i} \mid B\right)=\frac{P\left(B \mid A_{i}\right) P\left(A_{i}\right)}{\sum_{j} P\left(B \mid A_{j}\right) P\left(A_{j}\right)} \end{aligned}$$ 用图形表示就是:
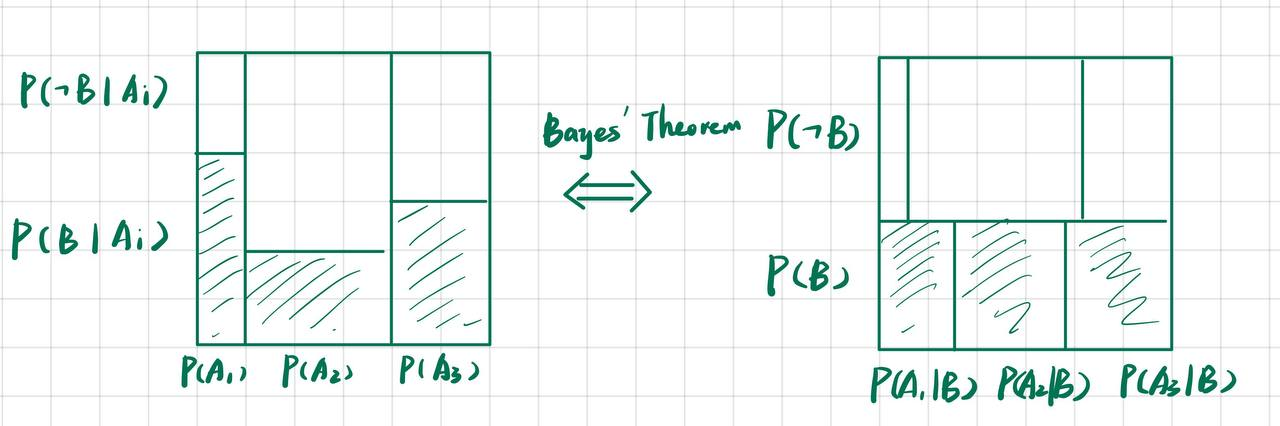
如果B分成了BCD三个互斥的情况, 用图形表示就是: