Diffie-Hellman问题
# Diffie-Hellman问题
# 两个Diffie-Hellman问题
# Computation Diffie-Hellman / CDH
即给定一个基数与两个指数, 计算合并的指数
- 给定$(\alpha, \alpha^b, \alpha^c)$, 求 $\alpha^{bc}$
# Decision Diffie-Hellman / DDH
即给你三个指数, 让你判断最后一个是不是前两个的合并
- 给定 $(\alpha^b, \alpha^c, \alpha^d)$, 判断有没有 $\alpha^d=\alpha^{bc}\space?$
注意: 给定的 $\alpha$ 是 $n$ 阶元素, 所以上面的运算都是 $mod\space \alpha^n$ 的
# 辨析: CDH / DDH
- CDH是计算一个数, DDH是判断计算结果是否成立
- 计算难度比较:
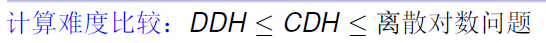 (来自课件)
(来自课件)
- 直觉上理解: 把可能的答案给出来了让你判断对不对(DDH)肯定比让你自己求答案(CDH)简单, 而要你把对数求出来(离散对数问题)是最难的, 因为和CDH相比, 这相当于先把每个部分的指数算出来, 再计算CDH里面的合并的元素(即先用$\alpha^b,\alpha^c$算$b,c$ 再计算$b\times c,$再算出$\alpha^{bc}$)
# DDH $\propto_T$ CDH $\propto_T$ Discrete Logarithm / 三个问题的图灵归约关系
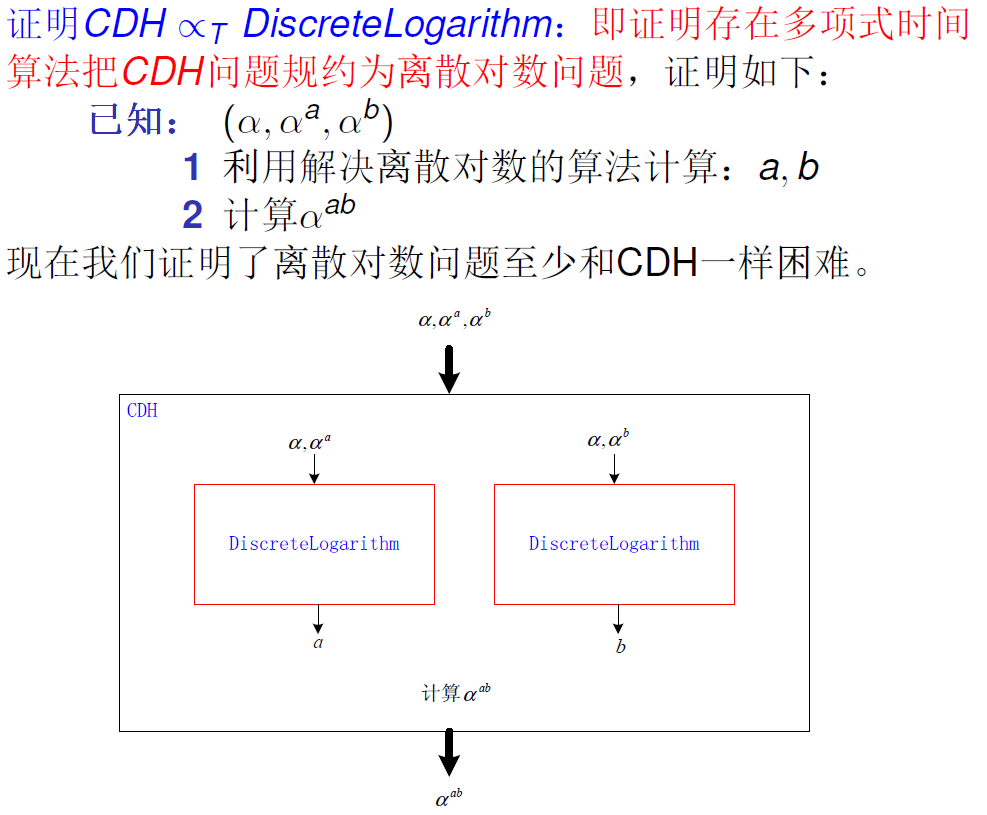
# CDH $\propto_T$ Discrete Logarithm
很简单, 正如前面已经提到的一样, 可以先用 $\alpha^b,\alpha^c$ 算 $b,c$ 再计算 $b\times c,$ 再算出 $\alpha^{bc}$.
CDH $\propto_T$ Discrete Logarithm 说明了 Discrete Logarithm 至少和 CDH 一样难
这样想更清晰: Discrete Logarithm至少比CDH难
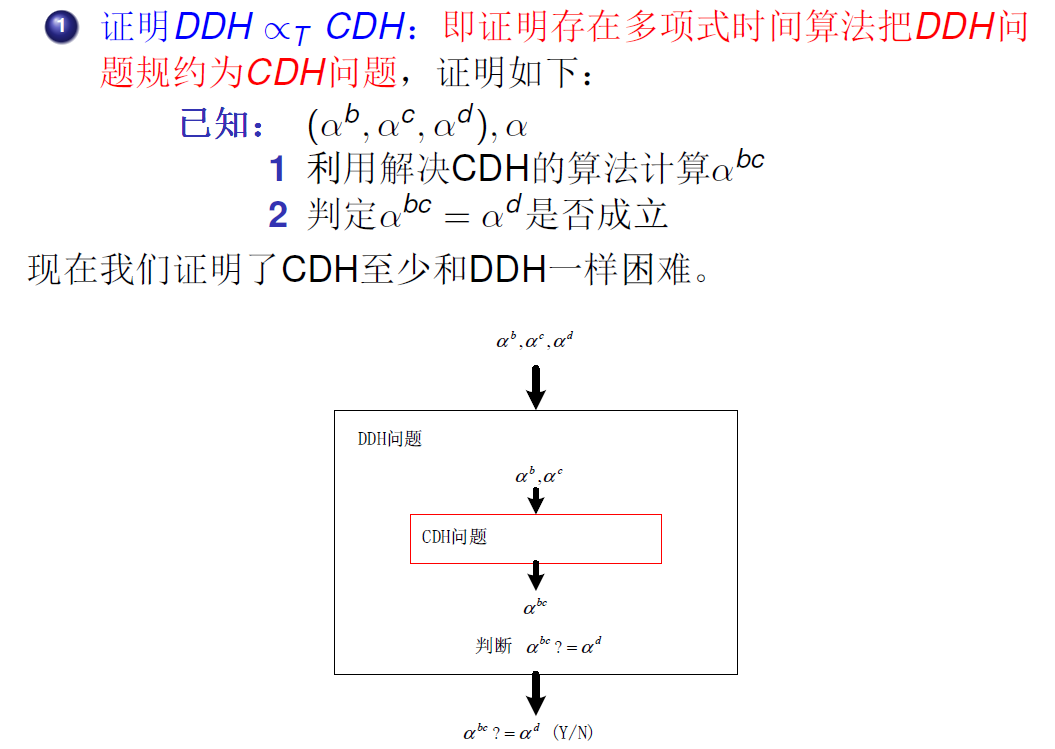
# DDH $\propto_T$ CDH
因为我们都可以求正确的$\alpha^{bc}$了,我们只需要验证$\alpha^{bc}$和$\alpha^{d}$是不是一样就可以解决DDH了
DDH $\propto_T$ CDH说明了CDH至少比DDH难
# 一个思考, DDH / CDH / Discrete Logarithm到底哪个最难?
一个错误想法:
有 DDH $\propto_T$ CDH,
说明 DDH 至少是和 CDH 一样难的(因为解决了 CDH 一定就可以解决 DDH)有 CDH $\propto_T$ Discrete Logarithm,
说明 CDH 至少是和 Discrete Logarithm 一样难的(因为解决了 Discrete Logarithm 一定就可以解决 CDH)
这样看来, 好像 Discrete Logarithm 最简单. CDH 第二简单, DDH 最难, 但是为什么实际是反过来的呢?
正确想法:
有DDH $\propto_T$ CDH, 说明CDH至少是和DDH一样难的(因为解决了CDH一定就可以解决DDH)
有CDH $\propto_T$ Discrete Logarithm, 说明Discrete Logarithm至少CDH是和一样难的(因为解决了Discrete Logarithm一定就可以解决CDH)
这样看来, Discrete Logarithm最难, CDH第二难, DDH最简单
……
CDH是和DLP相关的,但是哪个更难呢?如果我能有效率的解决DLP,那么我就可以找出$a$,然后轻松的计算出$g^{ab}$就像Bob做的那样,因此我们就解决了CDH.所以我们说能解决DLP那么一定能解决CDH,这就是说DLP至少和CDH一样难.
……
如果对手能够解决DDH(输出正确的x的概率大于1/2).那么就是说$G,g^a,g^b$一定泄露了一些关于$g^{ab}$的信息,使得攻击者能把它从随机的元素中分辨出来,尽管不能直接计算出来.而且很明显,如果对手能解决CDH问题,那么它可以有效率的解决DDH,因为它已经可以得到$g^{ab}$ 的值.这意味着,CDH至少和DDH一样难.
这就是我们这篇中讨论的三个问题,我们给出了一个简明的证明对他们的困难性进行排序:DLP最难,然后是CDH,最后是DDH.就像我们看到的那样,DLP有时候是简单的,会让CDH和DDH都变简单.因此群$G$和生成器$g$的选择在做密码学的时候是十分重要的!
# 解CDH的算法和解ElGamal的算法是等价的
in ElGamal:

注意$\alpha, \beta$都是公钥
$$ \begin{align} y_1&=\alpha^k\\ K&=\beta^k=\alpha^{ak}\\ y_2&=xK=x\beta^k=x\alpha^{ak}\\ &\Downarrow\\ x=d_k(y_1,y_2)&=y_2\cdot (\alpha^{ak})^{-1}=y_2\cdot (y_1^a)^{-1} \end{align} $$
# $OracleCDH\space\Rightarrow\space ElGamal$
$\delta=OracleCDH(\alpha,\beta,y_1)=OracleCDH(\alpha,\alpha^k,\alpha^k)$
由此算出 $\delta=\alpha^{ak}$,就相当于$y_1^a$了
所以$x=y_2\cdot\delta^{-1}$
# $CDH \quad\Leftarrow\quad OracleElGamal$
$$\begin{align} x&=OracleElGamal(\alpha,\beta,(y_1,y_2))\\ &=OracleElGamal(\alpha,\alpha^a,(\alpha^k,y_2))\\ &=y_2\cdot (\alpha^{ak})^{-1} \end{align} $$ 所以$\alpha^{ak}=y_2\cdot (y_2\cdot (\alpha^{ak})^{-1})^{-1}=\alpha^{ak}$