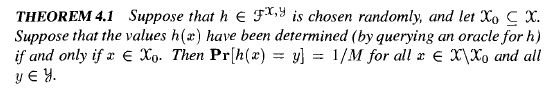Hash函数_Pt.2_攻击方法_安全性

Last updated Unknown Edit Source

• All
• Cryptography
• Course
• Hash

密码学原理与实践 page99

完全的随机对应性:

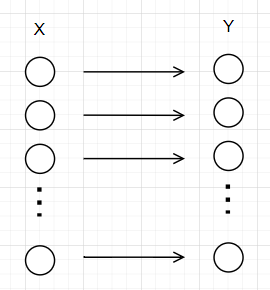
从名称来理解, 即理想的Hash函数相当于一个"先知", 能够对每一个$x$给出一个完全随机的$hash(x)$, 并且计算$hash(x)$的唯一方法便是询问Oracle(谕示器)

在这个假设下,有如下定理:

密码学原理与实践 page94

直观理解:

用一部分x去确定hash函数后,剩下的x取任意可能密文的概率是相同的.

即密文与明文的对应完全随机, 密文不取决于明文的任何性质(当然明文每次对应的密文得一样)

这就要求我们考虑如何设计一个hash函数, 既能保留某种 “独特性”, (即不能把所有的明文都对应到同一个密文上,不同的x对应不同的y)

又能保留某种 独立性 即x对应不同的y都是等概率的, 不能因为这个x的某些特征决定它取某些y的概率更高

在随机谕示模型下,我们对三种问题有以下算法: (注意,这些算法都是Las Vegas算法, 即不一定成功的算法) 我们规定这个算法最多计算Q次hash值, 这个算法的平均成功率为 $\varepsilon$

对于一个密文y,我们尝试用随机的Q个x去验证是不是y的原像

成功率: 1-Q次都找不到的概率 $$ 1-(1-\frac{1}{M})^Q $$

对于一个x,我们尝试用另外Q-1个$x^\prime$去验证是不是与x hash值相同

成功率:
1-(Q-1次都找不到的概率) $$ 1-(1-\frac{1}{M})^{Q-1} $$

验证 Q 个 x 中有没有 y 值相同的两个 x

成功率: 1-(Q个x hash值各不相同的概率) $$ 1-\frac{M}{M}\cdot\frac{M-1}{M}\cdots\frac{M-(Q-1)}{M} $$ 不要因为你不能控制碰撞对便认为碰撞问题没有实际威胁

从碰撞问题, 我们可以引出著名的生日悖论, 这两个问题在统计意义上是相同的, 即多个独立事件发生重复情形的概率 通过以下两个近似, 我们可以估算出样本总数(班级人数)与发生碰撞的概率(至少有两个人生日是同一天的概率)之间的关系:

最后的结果是: $$ Q \approx \sqrt{2 M \ln \frac{1}{1-\epsilon}} $$ 其中,M是所有可能的情形(一年中的365天), 如果我们取$\epsilon=0.5, Q\approx 22.3$即23人的班级里面就有50%的可能性有至少有两个人生日相同.

单独来看, 一个人取生日是一年中任意一天的概率是$\frac1{365}$, 是很小的, 但是当多个独立事件反复发生, 发生相同情形的"巧合"的概率却出奇的高(23个人相比365显然是很小的一个数)!

这个结论对于 Hash 函数的设计有什么启发意义呢?

所有可能的生日对应 Hash 函数的所有可能取值

班级人数则相当于上面算法里面的尝试次数Q

类似的, 如果我们的Hash函数的所有可能取值只有365个, 则只要尝试23次就很有可能找到一对hash值相同的数据了! 这显然不太安全(找到一对相同的看起来还不太严重,但是从下面的规约关系能看出, 解决了碰撞问题, 也解决了)

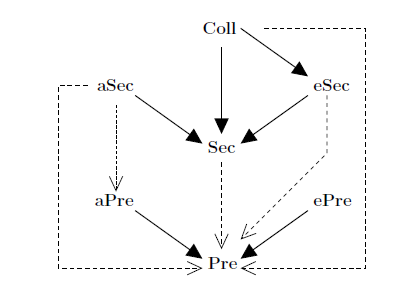
由上图中的箭头x–>y的含义是: if a hash function is secure in the $xxx$-sense, then it is secure in the $yyy$-sense.

书中下面两个问题的证明思路都是"逆否证法"

• 如果 碰撞稳固 则 第二原像稳固

证明方法:

证明如果有一个函数能够解决第二原像问题,则可以利用这个函数去解决碰撞问题 那么如果一个函数的碰撞问题不可被解决(即碰撞稳固),那么它的第二原像问题也不可被解决(也是第二原像稳固的).

注意: “解决碰撞问题"的含义是 “可以找到碰撞对” 而不是 “不会有碰撞了”

• 前提: $\bcancel{|\mathcal{X}|\geq 2|\mathcal{Y}|}$
• 如果 碰撞稳固 则 原像稳固–

注意： 不能这样说！书上只说明了如果我们有100%的把握解决原像问题，则有 $$ \mathcal{\frac{|X|-|Y|}{|X|}} $$ 的把握解决碰撞问题

而碰撞稳固（不能解决碰撞问题）并不能推出原像稳固（不能解决原像问题） （除非$\mathcal{X»Y}$, 即明文空间极大于密文空间)

  证明方法: 证明的是如果存在一个可以100%解决原像问题的Las Vegas算法，那么可以利用这个算法构造一个解决碰撞问题成功率是 $$ \mathcal{\frac{|X|-|Y|}{|X|}} $$ 的算法(在$|\mathcal{X}|\geq 2|\mathcal{Y}|$的时候把握是50%,如果$|\mathcal{X}|=|\mathcal{Y}|$则完全不可能找到碰撞

(为什么呢? 按理说如果有两个x指向同一个y,还是可以找到碰撞的啊?

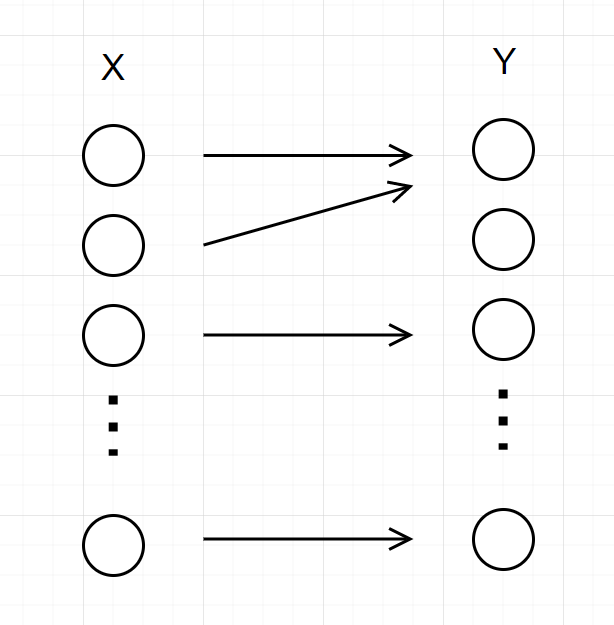
–>原因是在书中有这么一句话:

所以当$|\mathcal{X}|=|\mathcal{Y}|$的时候, x和y一定是一一对应的))