Hash函数_Pt.3_迭代Hash函数
# 迭代Hash函数
# 迭代Hash函数的基本结构
迭代Hash函数是一种用有限长度Hash函数来处理无限长度的数据的方法
下面这张图形象地表示了迭代Hash函数地加密步骤:
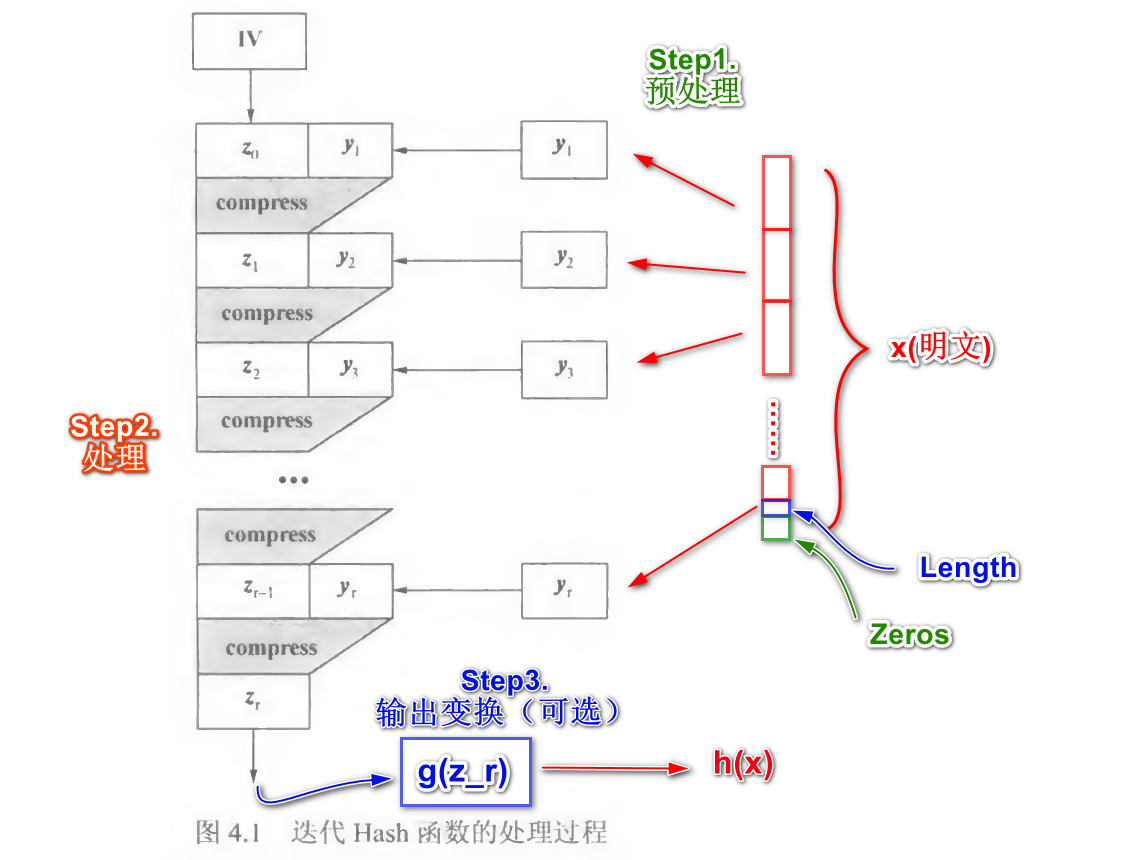
这样的构造方法可以概括为以下的三个步骤:
我们以有限的Hash函数$compress$为基础 $$ {0,1}^{m+t}\longrightarrow {0,1}^{m} $$ 这是一个将长度从$m+t$缩减到$m$的有限长度hash函数
- 预处理 这一步将明文切分成长度为t的小段.
–>最后剩余的怎么办?
在末尾添加整个字符串的长度
如果还不够,用0补足 –>为什么要添加字符串的长度? 这是为了使预处理函数$x\mapsto y$为单射, 保证整体的抗碰撞性质 反例:只添加0 1001_0 -> 1001_0000 1001_000 -> 1001_0000 这两个串构成了一个碰撞对
处理 这一步逐步循环调用$compress$, 知道得到最后的结果$z_r$,它的长度为$m$.
注意:
- 一开始有一个公开的初始值比特串 $IV$, 与$y_1$一同构成$compress$的第一次输入
- 我们每次缩减长度为t的串, 一共进行$$r\times t=\Big\lceil \frac{x}{t}\Big\rceil$$次,其中r是y的个数
- 输出变换 这一步把长度为$m$的结果映射到$l$, 使得最后的迭代Hash函数是一个长度上$i\mapsto l$的映射, i为任意自然数
- 这一步是可选的
# 迭代Hash函数的实例
# Merkle-Damgard结构
根据有限hash函数Compress中t的大小进行分类, Merkle-Damgard结构的函数有两种形式:
# Compress中 $t\geqslant2$ 的Merkle-Damgard结构
对比观察算法伪代码和图解即可(放大看)

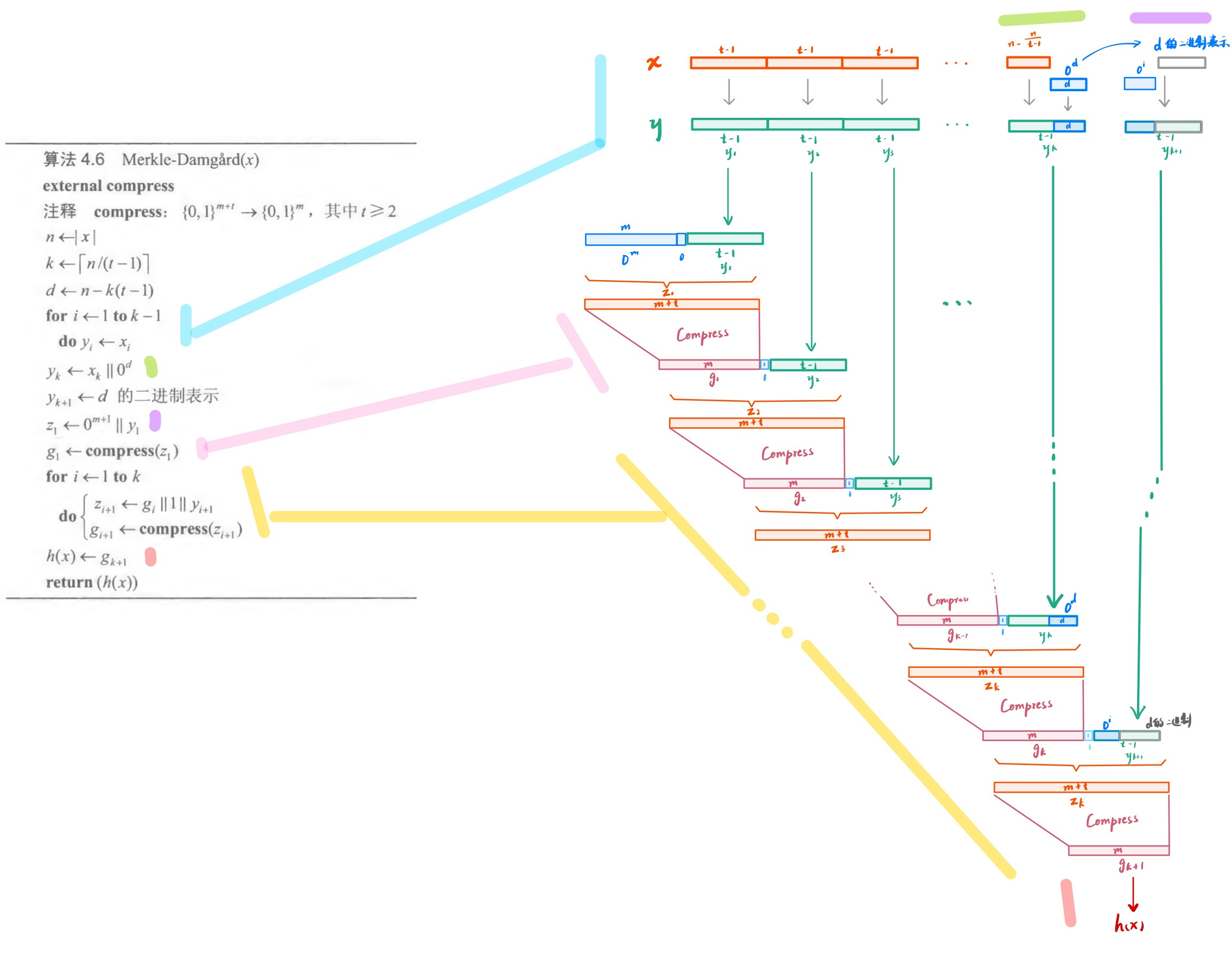
比较Merkle-Damgard结构和迭代Hash的一般结构:
- 预处理
- MD结构把x拆成了大小为t-1的小段(这也是为什么要单独讨论$t=1$ 的情形),否则$t-1=0,y$压根没法分
- 在最后补齐的时候是在末尾添上空缺位个数的二进制,在中间补零
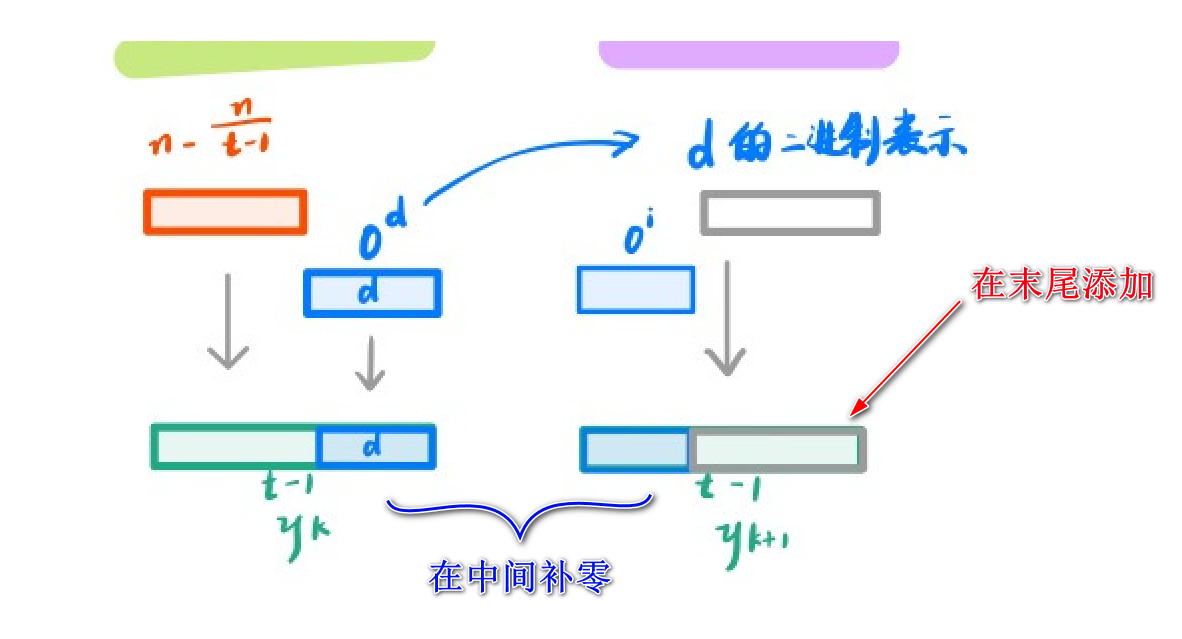
- 处理
- 在每次调用Compress的时候在最中间插入了一个1(注意是1个1不是0!) 对应t-1长度的y,每次Compress输入的长度依然是$m+t$
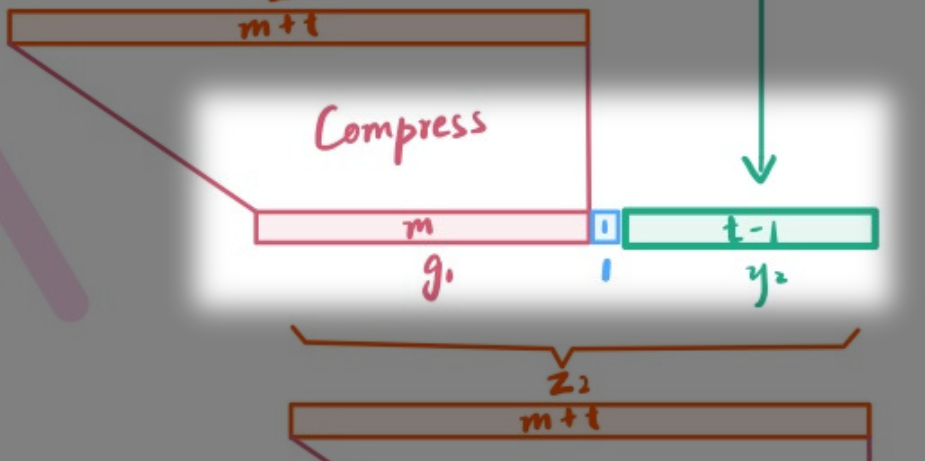
# Compress中 $t=1$ 的Merkle-Damgard结构
没法把x分成t-1长的小段了,我们怎么对x进行合理的拆分,方便我们利用Compress函数呢? 我们可以逐位对x进行某种代换,
# 论证迭代Hash函数的安全性
我们之前讨论的安全性只是针对于有限的Hash函数Compress的,但是我们可以将从这继续推广,得到迭代Hash函数安全性的一些结论
不是所有迭代Hash函数都有Merkle-Damgard结构的优秀性质:
杨礼珍老师课件 第 4 章 Hash 函数.Pdf#page=28
# Merkle-Damgard结构的安全性
# 碰撞稳固
- 如果Compress是碰撞稳固的,那么Merkle-Damgard函数也是碰撞稳固的
证明: 因为Merkle-Damgard结构有两种情形,所以也要分类讨论 我们证明的思路依然是”逆否证法“,即我们需要证明如果Merkle-Damgard结构中存在一个碰撞,那么Compress函数里面也一定可以找到一个碰撞
# $t\geq 2$的Merkle-Damgard结构
因为Compress是把原字符串分成许多小块进行Hash的,所以我们主要就是确定是在原字符串中的哪一部分能够找到一个”不一致“(碰撞) $$ \begin{array}{l} y(x)=y_{1}\left|y_{2}\right| \cdots | y_{k+1} \\ y\left(x^{\prime}\right)=y_{1}^{\prime}\left|y_{2}^{\prime}\right| \cdots | y_{\ell+1}^{\prime} \end{array} $$ 分类讨论:
- 在两个字符串长度模$t-1$结果不一样时, 很容易想到在最后添加的$y_{k+1}$一定不一样,这样Compress在最后一步一定有碰撞
情况 1: $|x| \equiv\left|x^{\prime}\right|(\bmod t-1)$ 。
这里 $d \neq d^{\prime}$ 且 $y_{k+1} \neq y_{l+1}^{\prime}$, 我们有
$$\begin{aligned} \operatorname{compress}\left(g_{k}|1| y_{k+1}\right) &=g_{k+1} \\ &=h(x) \\ &=h\left(x^{\prime}\right) \\ &=g_{\ell+1}^{\prime} \\ &=\operatorname{compress}\left(g^{\prime}l|1| y^{\prime}{\ell+1} \right) \end{aligned}$$
因为 $y_{k+1} \neq y_{\ell+1}^{\prime}$, 所以找到了 $h$ 的一个碰撞。
- 在最后找不到不一致, 就只有向前回溯. 现在两个字符串末尾一样(模$t-1$结果相同), 所以只有两种情形:
情况 2: $|x| \equiv\left|x^{\prime}\right|(\bmod t-1)$ 。 为了便于讨论,分成两种更细的情况:
- 两个字符串长度一模一样
- 两个字符串长度相差$t-1$的整数倍
- 对于第1种情形: 因为$z_1$在中间连接两个部分用的是0, 而剩下的$z$都用的是1, 所以在开头一定能找到一个碰撞.
情况 2a: $|x| \neq\left|x^{\prime}\right|$ 。 不失一般性,设 $\left|x^{\prime}\right|>|x|$, 因此 $\ell>k$ 。按照情况 $2 \mathrm{a}$ 类似的过程,假定没有找到 compress 的碰撞,最后总有 $$ \begin{aligned} \operatorname{compress}\left(0^{m+1} | y_{1}\right) &=g_{1} \\ &=g_{\ell-k+1}^{\prime} \\ &=\operatorname{compress}\left(g_{\ell-k}^{\prime}|1| y_{\ell-k+1}^{\prime}\right) \end{aligned} $$ 但 $$ 0^{m+1} | y_{1} $$ 的第 $(m+1)$ 比特是 0, 而 $$ g_{\ell-k}^{\prime}|1| y_{\ell-k+1}^{\prime} $$ 的第 $(m+1)$ 比特是 1 。因此必然会找到 compress 的一个碰撞。
- 对于第2种情形, 我们逐步倒推, 要么在某一步找到一个不一样, 要么没有不一样(而这与假设$y(x)\neq y(x^\prime)$ 相矛盾)
情况 2b : $|x|=\left|x^{\prime}\right|$ 。 此时有 $k=\ell$ 和 $y_{k+1}=y_{k+1}^{\prime}$, 像情况 1 中一样,我们有: $$ \begin{aligned} \operatorname{compress}\left(g_{k}|1| y_{k+1}\right) &=g_{k+1} \\ &=h(x) \\ &=h\left(x^{\prime}\right) \\ &=g_{k+1}^{\prime} \\ &=\operatorname{compress}\left(g_{k}^{\prime}|1| y_{k+1}^{\prime}\right) \end{aligned} $$ 如果 $g_{k} \neq g_{k}^{\prime}$, 则找到了 compress 的碰撞,所以可假定 $g_{k}=g_{k}^{\prime}$ 。则有 $$ \begin{aligned} \operatorname{compress}\left(g_{k-1}|1| y_{k}\right) &=g_{k} \\ &=g_{k}^{\prime} \\ &=\operatorname{compress}\left(g_{k-1}^{\prime}|1| y_{k}^{\prime}\right) \end{aligned} $$ 或者找到 compress 的一个碰撞,或者 $g_{k-1}=g_{k-1}^{\prime}$ 并且 $y_{k}=y_{k}^{\prime}$ 。假定没有找到碰撞,重复止 述过程,最后得到 $$ \begin{aligned} \operatorname{compress}\left(0^{m+1} | y_{1}\right) &=g_{1} \\ &=g_{1}^{\prime} \\ &=\operatorname{compress}\left(0^{m+1} | y_{1}^{\prime}\right) \end{aligned} $$ 如果 $y_{1} \neq y_{1}^{\prime}$, 则找到了 compress 的一个碰撞,因此可假定 $y_{1}=y_{1}^{\prime}$ 。这样对 $1 \leqslant i \leqslant k+1$ 都有 $y_{i}=y_{i}^{\prime}$, 所以 $y(x)=y\left(x^{\prime}\right)$ 。但因为映射 $x \mapsto y(x)$ 是单射,这意味着 $x=x^{\prime}$ 。而我们假定了 $x \neq x^{\prime}$, 这就产生了矛盾。
因为讨论了所有的情况,也就证明了所期望的结论。
其实这里不应该把书上的证明抄下来的, 这样降低了我的思考的浓度,让这篇笔记变得陌生了, 如果担心不够详细, 可以列出书上的页码, 在将来如果需要整理成文章,也可以到时候再来排版
# $t = 1$的Merkle-Damgard结构
关键:
- 逐比特预处理 预处理的关键便是如何在把长度变得规整的同时构造一个单射 先利用这个函数逐比特预处理: $$ \begin{align} f(0)&=0\\ f(1)&=01\\ \end{align} $$ 然后在开头添加11: $y\leftarrow 11||f(x_1)||f(x_2)||\cdots||f(x_n)$ (这是为了保证无碰撞性质, (构造无后缀性质保证无碰撞性质))
- 逐比特压缩 利用 $compress: {0,1}^{m+1}\rightarrow {0,1}^m$ 被压缩的第一个串是$0^m||y_1$