Hash函数_Pt.4_安全Hash算法_SHA-1

Last updated Unknown Edit Source

# SHA-1

Tags: #Cryptography #Math #Course #Hash

SHA-1是一个具有160bit消息摘要的迭代Hash函数

SHA-1 的分组大小是 512bit, 意味着每一次迭代处理 512bit 的数据

SHA-1建立在对比特串面向字的操作上, 意味着在处理512bit的时候是每次32bit, ~~一共16次~~, 一共80次. (为什么变多了? 因为在循环里面需要将16个字扩充到80个字, 如下图)

(刚开始我一直看不懂这里, 觉得数组下标超限了, 但仔细看, 意思其实是根据原来的16个字利用异或与循环左移构建新的字)

SHA-1在循环的时候使用了5个中间变量$A,B,C,D,E$, 大小为一个字, 不通过断更新它们的值来进行处理

Youtube - An Intuitive Introduction 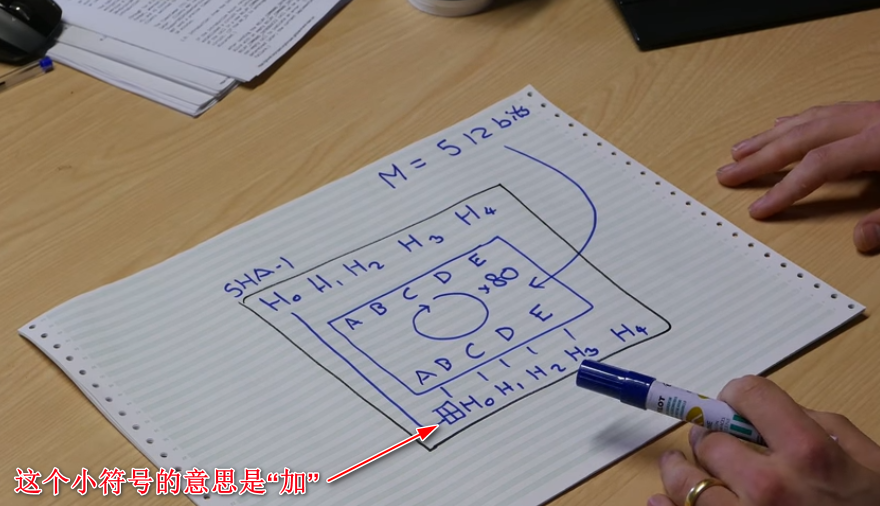同时这个视频里面还指出了其他地方都没有提到的一点: SHA-1 里面的所有加法都是循环加法(溢出位变成最低位), 这样会损失信息, 让 Hash 变得更安全.

(但是这一点其他地方都没有提到, 待验证!) #todo

老师的课件中把SHA-1与Merkle-Damgard结构的对应关系写的很清晰

红色"do"里面的部分如下图例:

注意的一点是SHA-1能处理的串是有最大长度的, 为$2^{64}-1$

同时因为在预处理的时候需要填充x的长度$l$, 从上面可以知道$|l|\leq 64\space bits$, 如果$l$长度不够, 在左边加0, (在左边加0也符合正常的大小表示方法(用0 填充没有用到的高位))

预处理方法: $$y\leftarrow x||一个1||许多0||l$$ 0 有多少个呢? 让 y 的长度 mod 512=0 即可

更清晰一点的话, 是:

|480