Hash函数_Pt.5_消息认证码_MAC
# 消息认证码 MAC Message Authentication Code
# 消息认证码是什么
生成方式: 带密钥的Hash函数, Hash值可以不用在安全的信道上传输, 只需要开始的时候协商一个密钥$K$就可以了
用于核验在不安全信道上传输的消息有没有被修改
# 不安全的构造方式
一个很直观的方式便是把密钥$K$加到明文x里面,一起Hash, 既然攻击者不知道$K$是什么, 他也应该无法计算$h_K(x)=h(x_K). (x_K$为加入了K的x)
但是以下论证告诉我们一些简单的构造方式并不安全, 攻击者即使不知道K是什么, 也可以利用一个有效对$(x,h_K(x))$计算新的有效对$(x^\prime,h_K(x^\prime)$
# 直接把K作为$IV$
(IV 即 Compress 的初始输入 见迭代Hash函数的基本结构)
# 无预处理
假设$x^{\prime}=x||w$, 则可以这样计算新的$h_K(x^\prime)$ $$h_{K}\left(x | w\right)=\operatorname{compress}\left(h_{K}(x) | w\right)=\operatorname{compress}\left(y| w\right)$$
直觉理解: 为什么还是能够算出新的有效对, 即使我们并不知道K? 这说明这种构造方式没有很好的隐藏K, 我们以为K,没有泄露, 其实K是隐藏在$h_K(x)$里面的
# 有预处理(padding)
我们还是能够计算$h_K(x||pad(x)||w||(pad(x^\prime))$此时$x^\prime=x||pad(x)|w$
# 嵌套MAC和HMAC
嵌套 MAC 即合成两个带密钥的 Hash 族来建立一个 MAC 算法
$$(g \circ h){(K, L)}(x)=h{L} \left(g_{K}(x)\right)$$
外面的$h_L$是一个安全的"小MAC", 里面的$g_K$是一个碰撞稳固的带密钥的Hash族, 它们共同构建了一个安全的"大MAC" $\Rightarrow$ “大 MAC”=先带密钥 Hash, 再生成 MAC
# 对嵌套MAC的攻击
有三种攻击方式 , 分别是:
- 对嵌套MAC的假冒者(“大MAC攻击”)$\longrightarrow$(直接攻击整个, 企图找到$x^\prime$ 的$h_{L}(g_{K}(x^\prime))$)
- 对小MAC的假冒者(“小MAC攻击”)$\longrightarrow$(攻击$h_L$, 即攻击外层的MAC, 对于$x^\prime$ ,企图找到$h_{L}(x^\prime)$
- 当密钥是保密的,对Hash族的碰撞-探测者(“未知-密钥碰撞攻击”)$\longrightarrow$(攻击$g_K$, 即攻击内层的的MAC, 对于$x^\prime$ ,企图找到$h_{L}(x^\prime)$( 之前讨论过的碰撞问题)
书上证明了一个结论, 这个结论说明:
如果对小MAC的攻击至多有$\epsilon_2$的成功率, 对Hash函数的(不知道密钥的)碰撞攻击最多有$\epsilon_1$的成功率, 那么对总的嵌套MAC的攻击至多有$\epsilon_1+\epsilon_2$的成功率
(即$\epsilon\leqslant \epsilon_1+\epsilon_2$)
# HMAC
HMAC是利用不带密钥的Hash函数构造的嵌套MAC
下面是利用
SHA-1构造的HMAC:
$$
\operatorname{HMAC}_{K}(x)=\mathrm{SHA}-1((K \oplus \text { opad }) | \mathrm{SHA}-1((K \oplus \text { ipad }) | x))
$$
其中, 密钥K的长度是512bits,

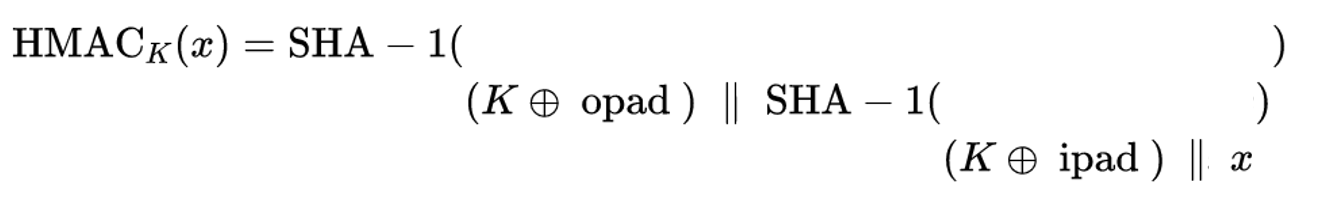
总体上来看, HMAC把密钥与两个常数异或构成两个新的密钥 , 然后分别放入嵌套的SHA-1中与明文一起进行加密, (处理后的密钥放在前面)
注意第二次计算仅仅需要利用一次Compress, 所以HMAC也相当于
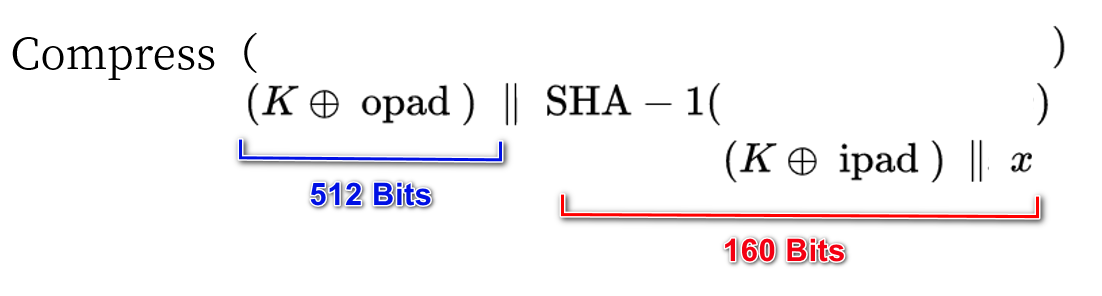
# CBC-MAC
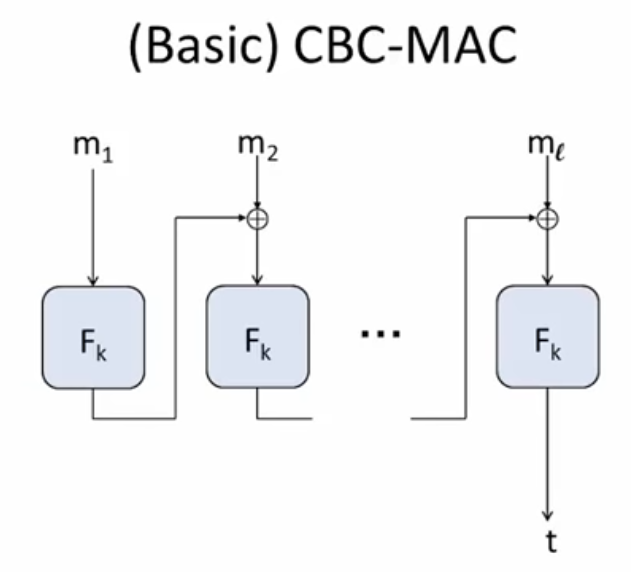
CBC-MAC和DES/AES的CBC工作模式非常相似, 这是一种由分组密码构造MAC的方式.
杨礼珍老师课件 第 4 章 Hash 函数.pdf#page=47
其实IV相当于没有, 因为$0^t\oplus x_1=x_1$
Nice Youtube Video
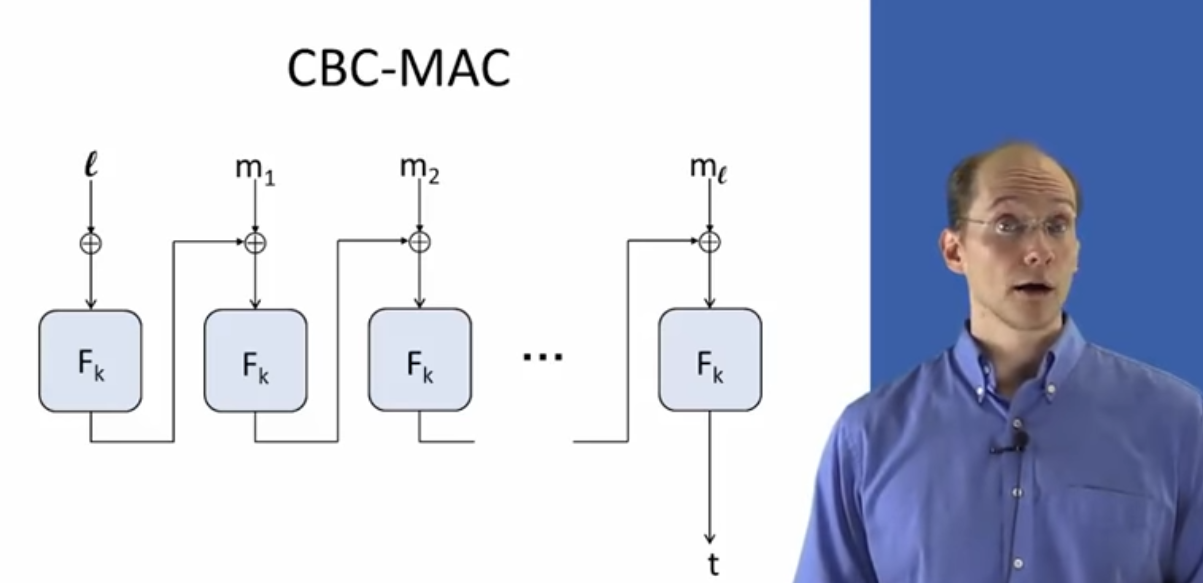
 在视频里面强调了, 如果你引入了IV, 反而会损失安全性
在视频里面强调了, 如果你引入了IV, 反而会损失安全性
这个带长度的没看懂 #没看懂
 生日攻击没看懂
生日攻击没看懂