Different_Gradient_Descent_Methods
# Batch Gradient Descent, 批梯度下降, BGD
每一次把所有数据都用来更新参数, Use ALL the training examples. $$ \begin{array}{l} \text { repeat until convergence }{\\ \begin{array}{cc} &\theta_{j}:=\theta_{j}-\alpha \frac 1 m \sum_{i=1}^{m} \left(h_{\theta}(x^{(i)})-y^{(i)}\right) x_j^{(i)} \end{array}\\ \text { } } \\\ \text { (simultaneously update } j=0, \cdots ,j=n) \end{array} $$
# Stochastic/Incremental Gradient Descent, 随机梯度下降 SGD
$$ \begin{aligned} Loop &\quad {\qquad\\ &\text { for } \mathrm{i}=1 \text { to } \mathrm{m},{ \\ &\qquad \theta_{j}:=\theta_{j}+\alpha\left(y^{(i)}-h_{\theta}\left(x^{(i)}\right)\right) x_{j}^{(i)} \qquad\quad(\text { for every j} \space )\\ \quad&\qquad\quad}\\ &\quad} \end{aligned} $$ 上面这个式子最大的不同是: 没有了求和符号, 取而代之的是一个for循环. 这意味着随机梯度下降每一次只根据一个样本进行参数更新.(each time we encounter a training example, we update the parameters according to the gradient of the error with respect to that single training example only.)
这样的好处是速度快, 每一次计算都在更新参数, 而不像BGD那样把所有样本都算一遍才能更新一次参数. 坏处是可能不会Converge, 最终得到的结果可能只是一个近似解, 最后得到一种震荡的状态. 一种解决方法是随着训练的进行不断减小学习率, 这样便可以增大收敛的几率.
# Mini-batch Gradient Descent
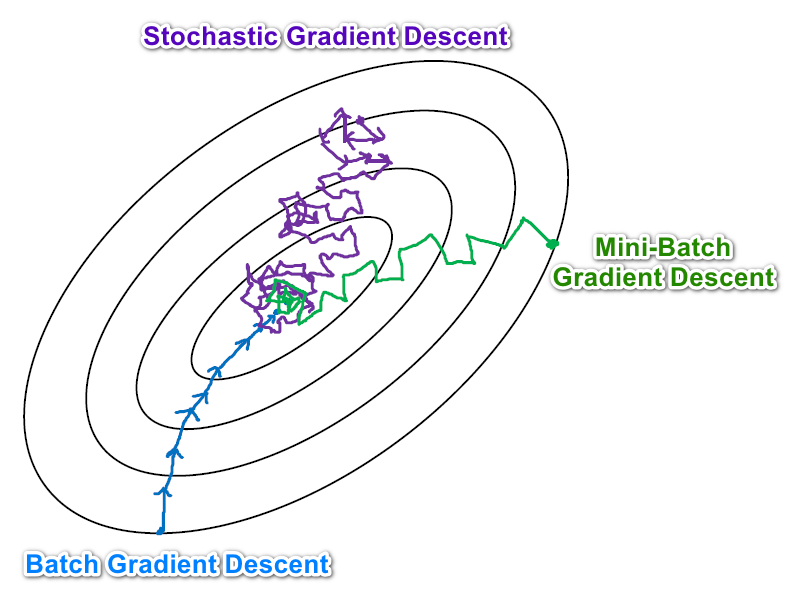
这种方法综合了上面两种方法的优缺点, 每次选一个小样本来更新参数, 达到了一个很好的折中.
# Other Methods
其实还有很多方法, 这篇文章是一个很好的总结.
吴恩达的深度学习课程里面有一节专门讲优化方法: #todo https://www.coursera.org/lecture/deep-neural-network/mini-batch-gradient-descent-qcogH ^06f99c