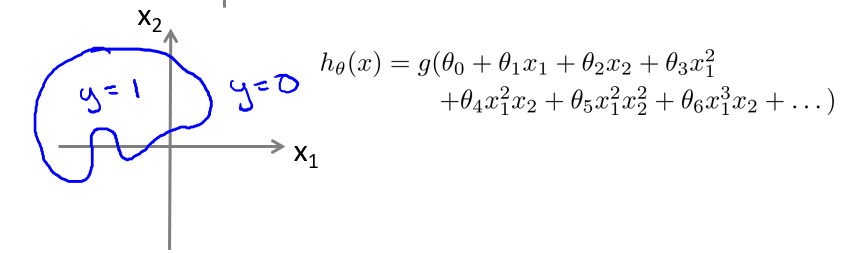Part.12_Logistic_Regression(ML_Andrew.Ng.)
# Logistic Regression
Tags: #LogisticRegression #MachineLearning #Classification
# Logistic Function
# Hypothesis Representation
我们可以通过对线性回归的方法进行一些小改动来匹配回归问题, 在线性回归的时候, $h(x)$的输出与分类问题的"值域"偏差较大, 比如在二分类问题里面, 要求$y=0\space or\space 1$, 但是$h(x)$会输出大于一或者小于零的数.
为了解决这个问题, 我们将$h(x)$作为逻辑斯蒂函数的输入, 将任意输出匹配到$(0,1)$区间里面去, 方便分类. $$\begin{aligned} &h_{\theta}(x)=g\left(\theta^{T} x\right) \\ &g(z)=\frac{1}{1+e^{-z}}\\ &z=\theta^{T} x \\ \end{aligned}$$
Hypothesis如此表述之后, $h(x)$的值就可以理解为二分类问题中, $x$被归为$1$的概率大小. 严谨的表述是: $$h_θ(x)=P(y=1|x;θ)=1−P(y=0|x;θ)$$ $$P(y=0|x;θ)+P(y=1|x;θ)=1$$ 其中 " $;θ$ " 的含义是: $θ$是参数(Parameterized by theta).
# Decision Boundary
假如我们采用这样的分类方法: $$\begin{aligned} &h_{\theta}(x) \geq 0.5 \rightarrow y=1 \\ &h_{\theta}(x)<0.5 \rightarrow y=0 \end{aligned}$$
那么分类结果最终由$h(x)$的值决定: $$\begin{aligned} θ^Tx≥0⇒y=1\\ θ^Tx<0⇒y=0 \end{aligned}$$
一个例子:
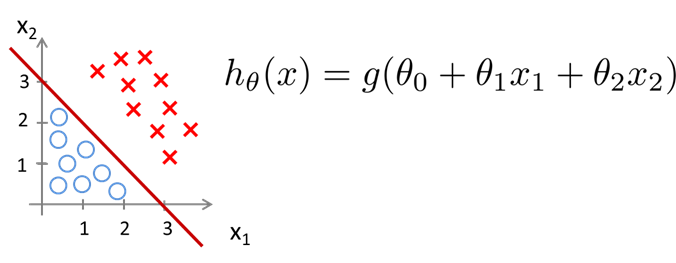图中划分数据集的线便是这个$h(x)$, Decision Boundary, 在曲线上面的点$h(x)\geq 0$, 分类结果为1, 在曲线下面的点$h(x)< 0$, 分类结果为0.
注意Decision Boundary是$h(x)$的性质, 即使上图不画数据点, Boundary依然存在.
# Nonlinearity
就像线性回归可以推广为多项式回归一样, Logistic 回归也可以有非线性的决策边界:
