Part.13_Cost_Function-Logistic_Regression(ML_Andrew.Ng.)

Last updated Aug 19, 2021 Edit Source

• All
• Cost function
• Logistic regression
• Machine learning

Tags: #CostFunction #LogisticRegression #MachineLearning

如果我们采用 线性回归的损失函数: 均方误差, 那么因为Logistic 回归的$h(x)$里面有形式很复杂的Logistic函数, 损失函数将不再是 凸函数, 将会很难最小化, 所以我们需要考虑另外的损失函数形式:

我们采用这样的对数形式 Update: 这其实是 Cross_Entropy-交叉熵

$$ \begin{array}{ll} J(\theta)=\frac{1}{m} \sum_{i=1}^{m} \operatorname{Cost}\left(h_{\theta}\left(x^{(i)}\right), y^{(i)}\right) & \\ \\ \operatorname{Cost}\left(h_{\theta}(x), y\right)=-\log \left(h_{\theta}(x)\right) & \text { if } \mathrm{y}=1 \

\operatorname{Cost}\left(h_{\theta}(x), y\right)=-\log \left(1-h_{\theta}(x)\right) & \text { if } \mathrm{y}=0 \end{array}$$

• 在$y=1$时: 我们的损失函数在接近0的时候(错误的一端)趋向于无穷大, 在等于1的时候(正确的一端)达到最小值0. $$\operatorname{Cost}\left(h_{\theta}(x), y\right)=-\log \left(h_{\theta}(x)\right) $$

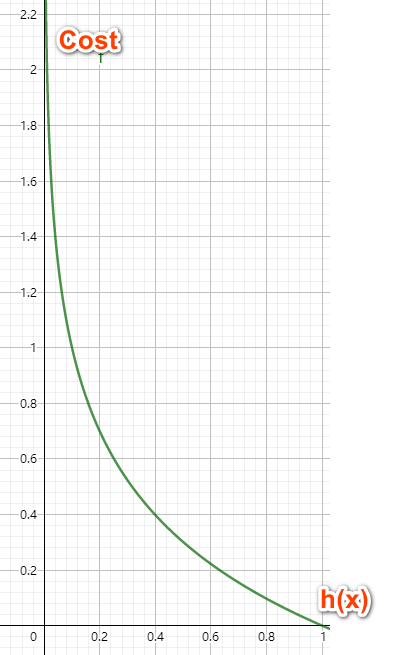
• 在$y=0$时: 我们的损失函数在接近1的时候(错误的一端)趋向于无穷大, 在等于0的时候(正确的一端)达到最小值0. $$\operatorname{Cost}\left(h_{\theta}(x), y\right)=-\log \left(1-h_{\theta}(x)\right) $$

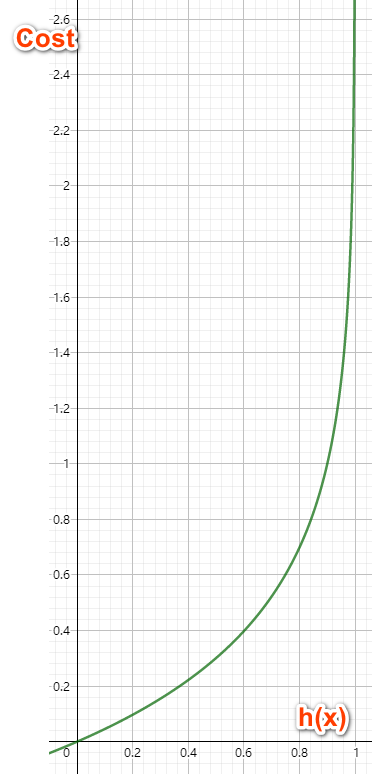
这样, 总体上, 在预测值与真实值越接近的时候损失函数越接近于0.

$$\begin{array}{ll} Cost(h_θ(x),y)=0 \text{ if } h_θ(x)=y\\ Cost(h_θ(x),y)→∞ \text{ if } y=0 \text{ and } h_θ(x)→1\\ Cost(h_θ(x),y)→∞ \text{ if } y=1 \text{ and } h_θ(x)→0\\ \end{array}$$

这样的损失函数形式确保了logistic regression的 $J(θ)$ 是凸函数.

证明Logistic回归的损失函数是凸函数

我们可以把两种情况写成一个式子: $$\operatorname{Cost}\left(h_{\theta}(x), y\right)=-y \log \left(h_{\theta}(x)\right)-(1-y) \log \left(1-h_{\theta}(x)\right)$$ (观察上面的式子: 在$y=1$的时候, $1-y=0$, 在$y=0$的时候, $1-y=1$)

所以损失函数可以表示为: $$ \begin{align} J(\theta)&=\frac{1}{m} \sum_{i=1}^{m} \operatorname{Cost}\left(h_{\theta}\left(x^{(i)}\right), y^{(i)}\right) \\ &=-\frac{1}{m} \sum_{i=1}^{m}\left[y^{(i)} \log \left(h_{\theta}\left(x^{(i)}\right)\right)+\left(1-y^{(i)}\right) \log \left(1-h_{\theta}\left(x^{(i)}\right)\right)\right]\\ \end{align} $$ (注意提出来的负号)

向量化的表示为: $$ \begin{aligned} h&=g(X \theta) \\ J(\theta)&=-\frac{1}{m} \cdot\left[y^{T} \log (h)+(1-y)^{T} \log (1-h)\right] \end{aligned} $$