Part.3_Linear_Regression(ML_Andrew.Ng.)

Last updated Jul 31, 2021 Edit Source

• All
• Machine learning
• Self learning

Tags: #MachineLearning #SelfLearning

• Supervised Learning
• Regression Problem

基于训练集, 我们希望通过学习算法得到一个Hypothesis函数$h$, 在房价预测问题上. 输入房子的大小, 得到估计的价格. 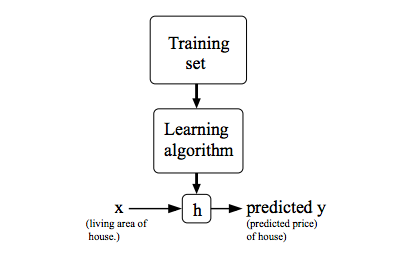对于单变量的线性回归问题(Univariate Linear Regression), 可以表现为如下形式: $$ h_\theta(x)=\theta_1 x+\theta_0$$ 其中$h_\theta$可以简记为$h$

对于训练数据:

• A pair $(x^{(i)} , y^{(i)} )$ is called a training example

• The dataset that we’ll be using to learn—a list of m training examples $(x^{(i)},y^{(i)})\space , (i=1,…,m)$ — is called a training set.

损失函数是用来衡量Hypothesis function的精确度的, 损失函数可以衡量Hypothesis在整个数据集上面平均误差

下面是一个名叫" 平方误差函数/Squared Error Function/Mean Squared Error“的损失函数: $$J\left(\theta_{0}, \theta_{1}\right)=\frac{1}{2 m} \sum_{i=1}^{m}\left(\hat{y}^{(i)}-y^{(i)}\right)^{2}=\frac{1}{2 m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2}$$ 分开来看, $J\left(\theta_{0}, \theta_{1}\right)$实际上是$\frac 1 2\overline{x}$, $\overline{x}$是预测值与真实值误差的平方

Link: Why_do_cost_functions_use_the_square_error

Part.4_Cost_Function_Intuition

• Our hypothesis function need not be linear (a straight line) if that does not fit the data well.
• We can change the behavior or curve of our hypothesis function by making it a quadratic, cubic or square root function (or any other form).