Part.4_Cost_Function_Intuition(ML_Andrew.Ng.)
# Cost Function Intuition: Linear Regression
2021-08-02
Tags: #MachineLearning #CostFunction #LinearRegression
# 2-Dimension Intuition
首先简化一下我们的问题, 现在只有三个数据点$(1,1),(2,2),(3,3)$, 我们的Hypothesis Function$:h=\theta_1 x$ 只有一个参数$\theta_1$表示斜率, Cost Function还是:
$$
J\left(\theta_{0}, \theta_{1}\right)=\frac{1}{2 m} \sum_{i=1}^{m}\left(\hat{y}^{(i)}-y^{(i)}\right)^{2}=\frac{1}{2 m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2}
$$
则我们大概可以把Cost Function的变化过程表示成这样:
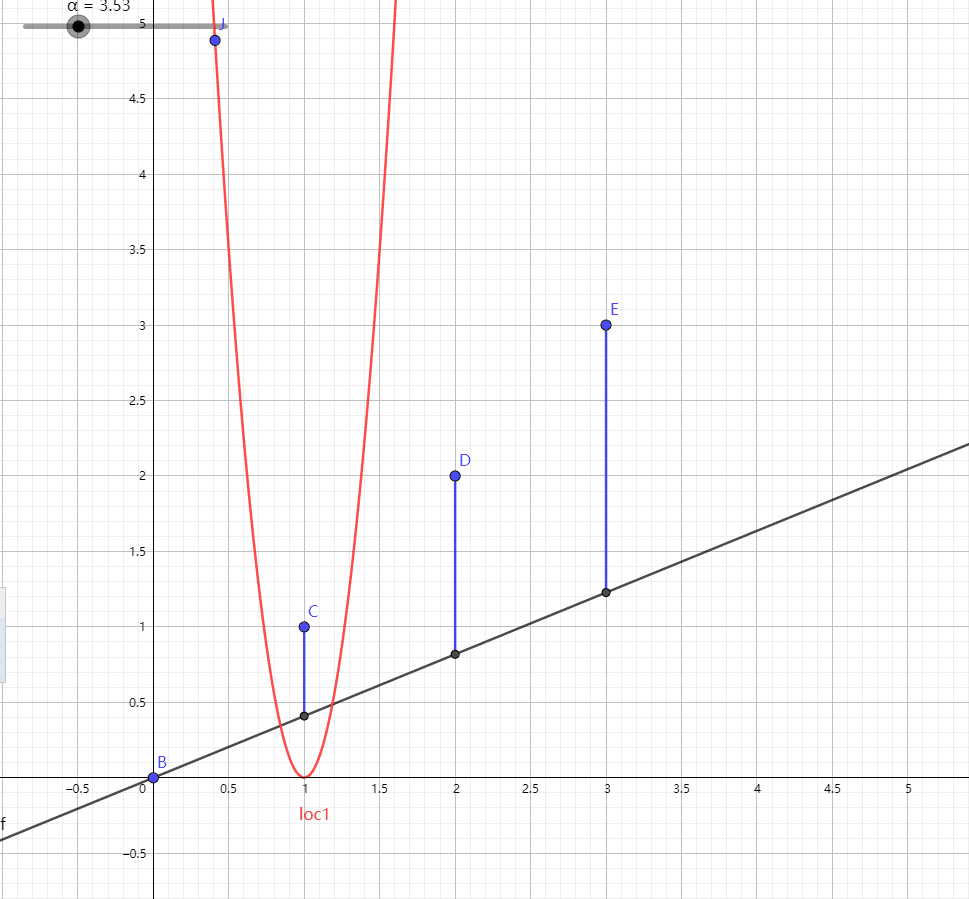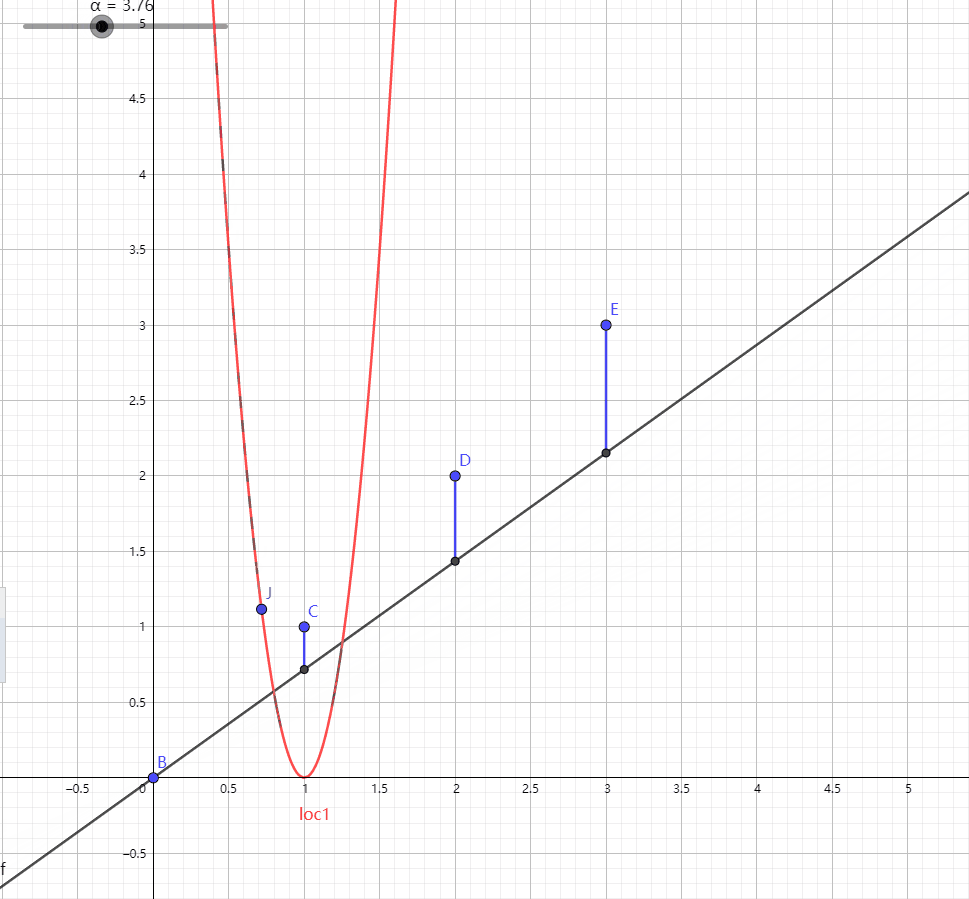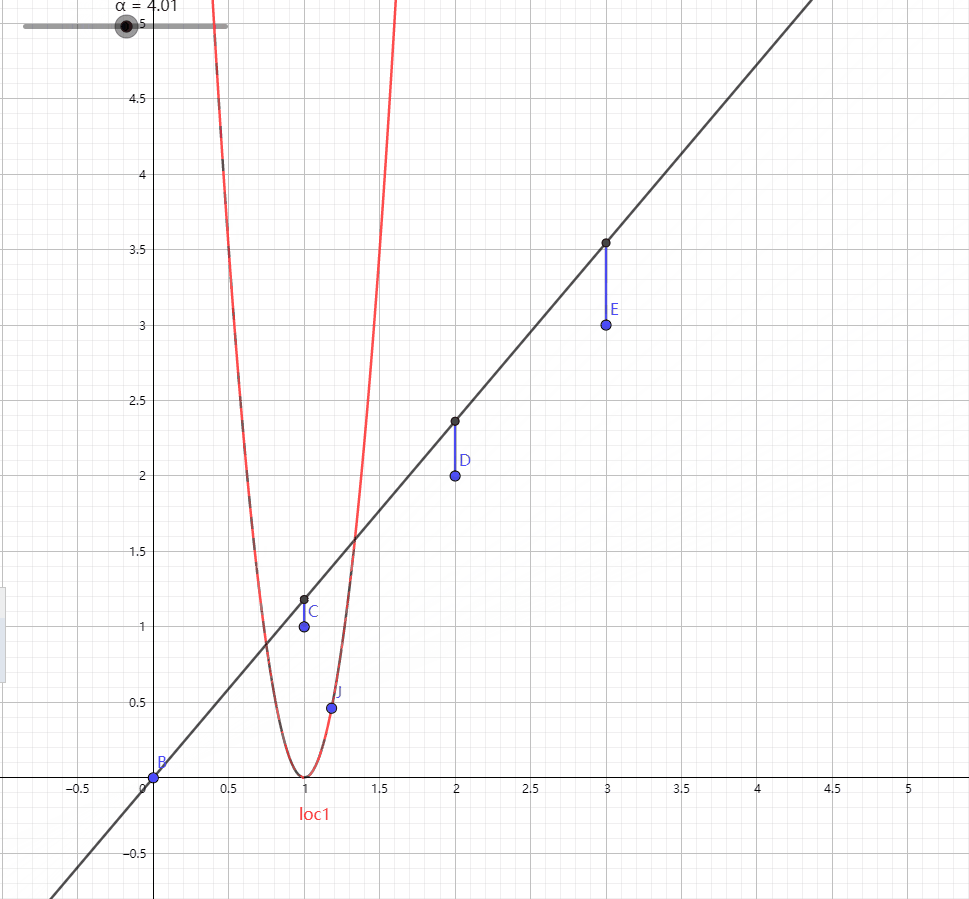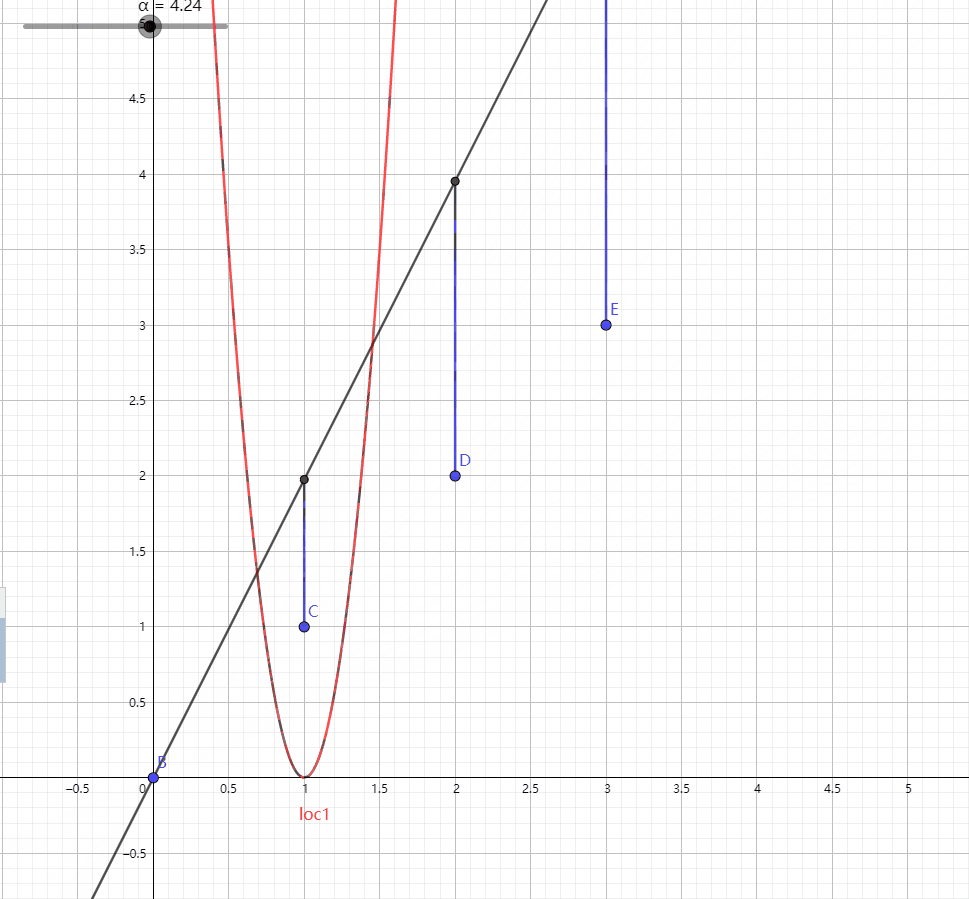可以看出, 斜率为1的时候Cost Function有最小值1, 此时Hypothesis最优.
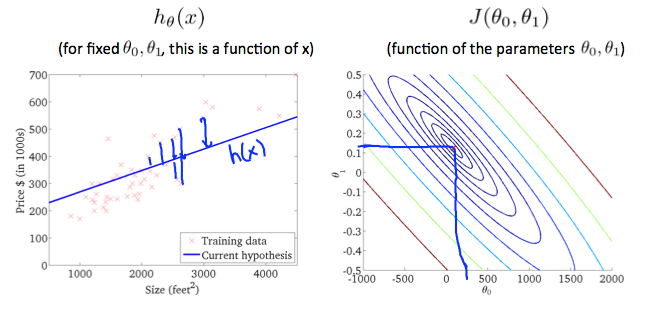
# 3-Dimension Intuition
三维的情况即Cost有两个参数$\theta_0, \theta_1$, 如果$z$轴表示Cost Function的大小那么会是一个碗装的曲面, 表示在一个平面里面可以用等高线图(Contour Map)来表示.
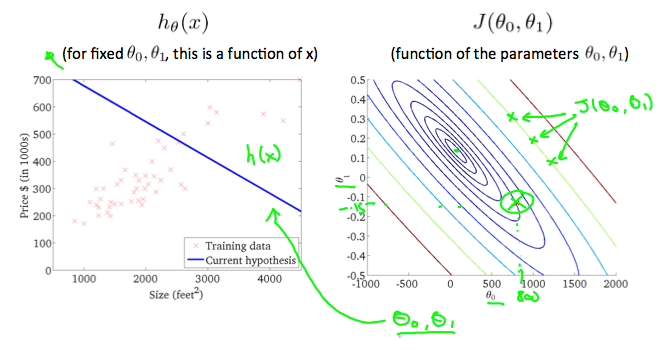最优的情况即曲面的最低处
