Part.5_Gradient_Descent(ML_Andrew.Ng.)
# Gradient Descent
Tags: #MachineLearning #GradientDescent
梯度下降是一种最小化损失函数的标准方法 So we have our hypothesis function and we have a way of measuring how well it fits into the data. Now we need to estimate the parameters in the hypothesis function. That’s where gradient descent comes in.
# Intuition
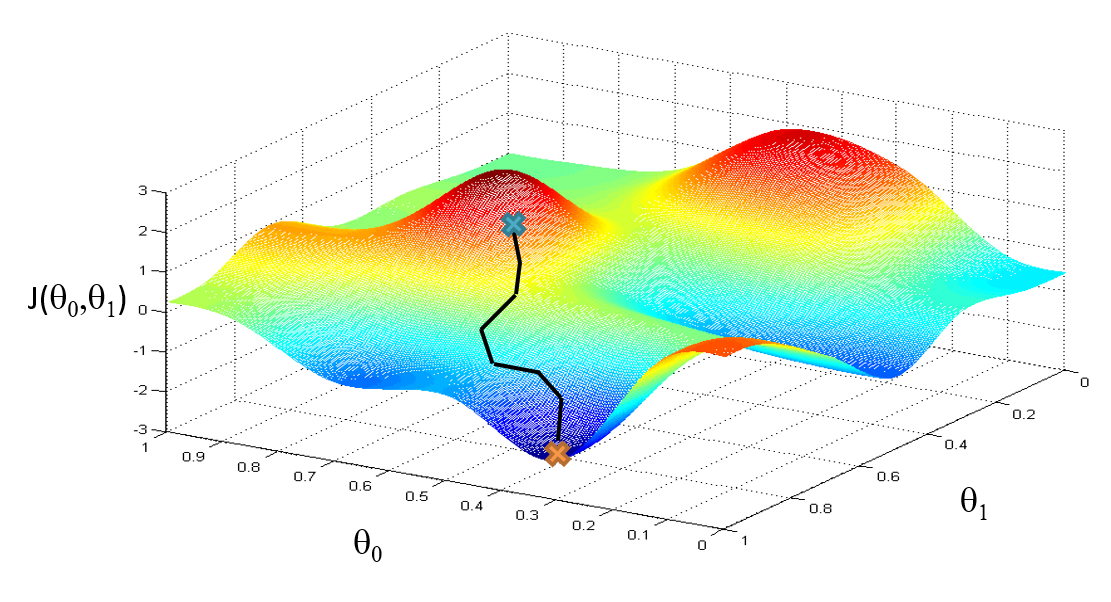 这个曲面是在CostFunction空间里面的, XY坐标表示Hypothesis里面的参数$\theta_0,\theta_1 \cdots$
CostFunction代表Hypothesis与真实值的偏差, CostFunction的目标是使自己的值最小, 即Hypothesis与真实值的偏差最小.
更新哪个参数就相当于在那个参数的方向上走一步.
这个曲面是在CostFunction空间里面的, XY坐标表示Hypothesis里面的参数$\theta_0,\theta_1 \cdots$
CostFunction代表Hypothesis与真实值的偏差, CostFunction的目标是使自己的值最小, 即Hypothesis与真实值的偏差最小.
更新哪个参数就相当于在那个参数的方向上走一步.
# Algorithm
$$ \begin{array}{l} \text {repeat until convergence }{\\ \begin{array}{cc} \theta_{j}:=\theta_{j}-\alpha \frac{\Large\partial}{\Large\partial \Large\theta_{j}} J\left(\theta_{0},\cdots ,\theta_{n}\right) & \text { (simultaneously update } j=0, \cdots ,j=n) \end{array}\\ \text { } } \end{array} $$
- 里面的$:=$表示"赋值"
# Learning Rate / 学习率
即每一步的长度
- 每一步长度的比例大小, 上方公式里面的 $\Large\alpha$
- 相当于一个人腿的长度, 并不能直接等同于每一步的长度, 因为每一步的长度还和偏导数的大小有关

# No need to decrease Learning Rate overtime
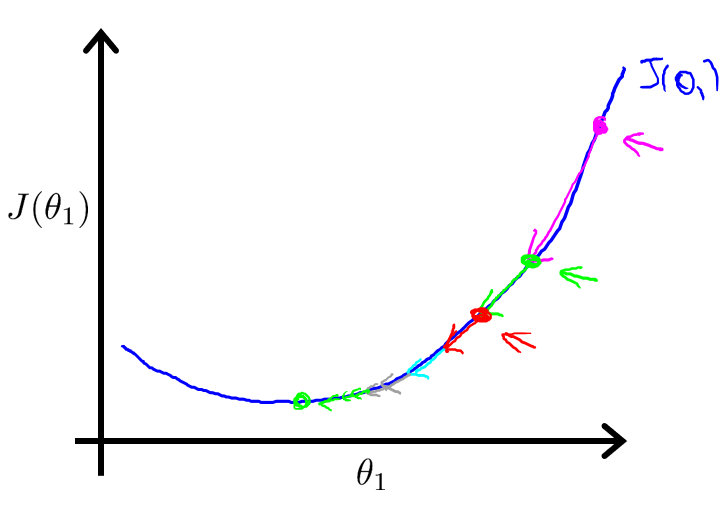
As we approach a local minimum, gradient descent will automatically take smaller steps. So, no need to decrease α over time.
# 合理调整学习率
调整每一步的大小比例
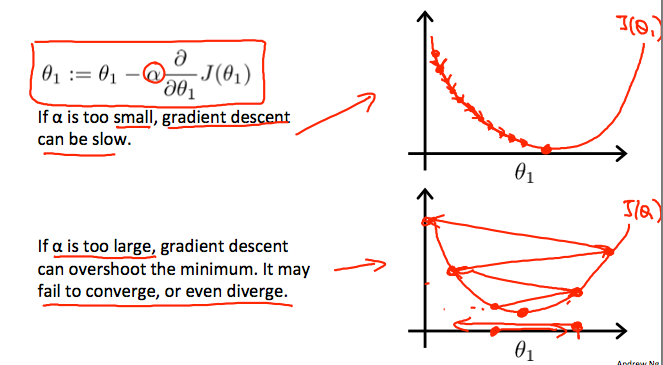
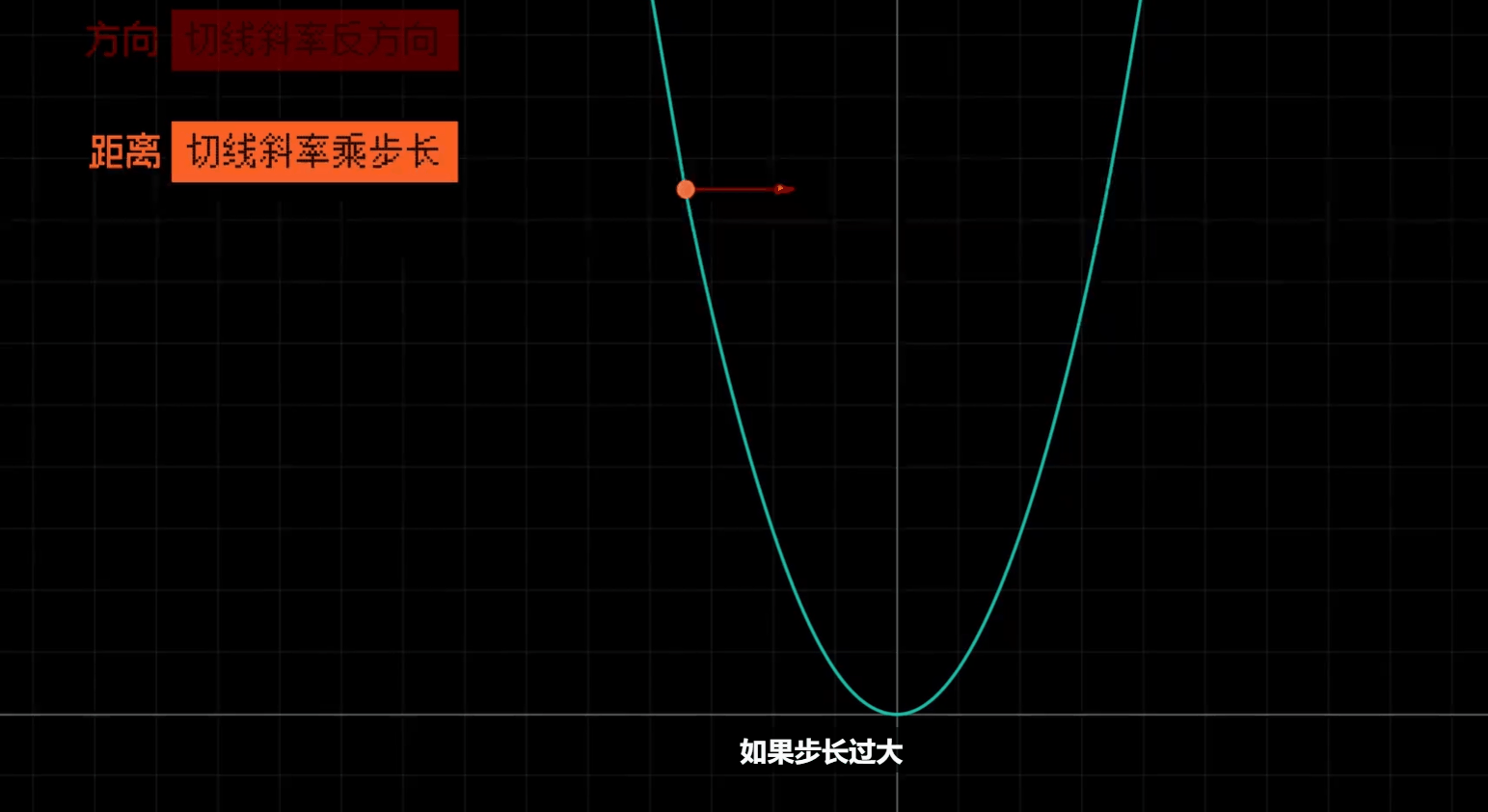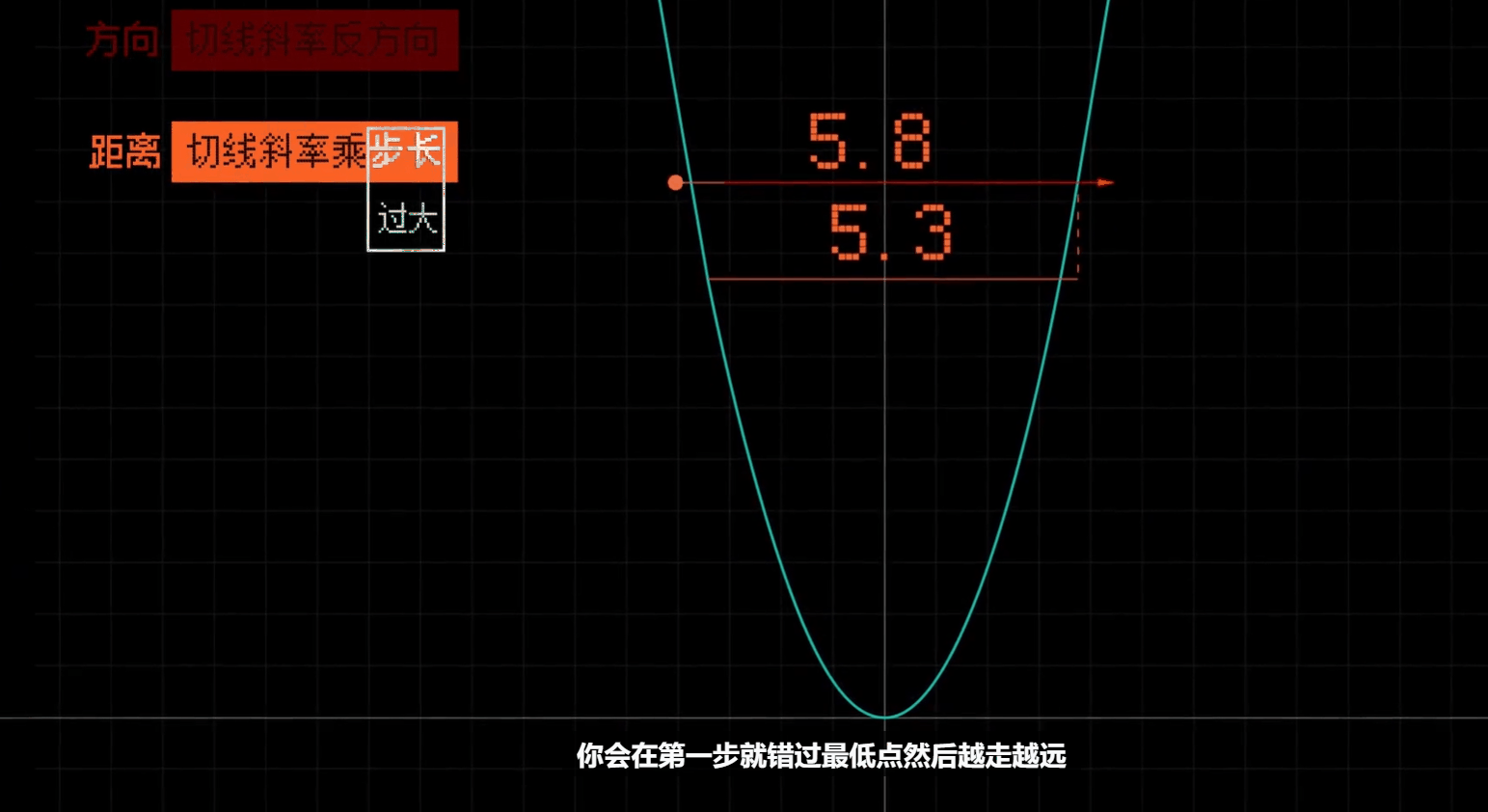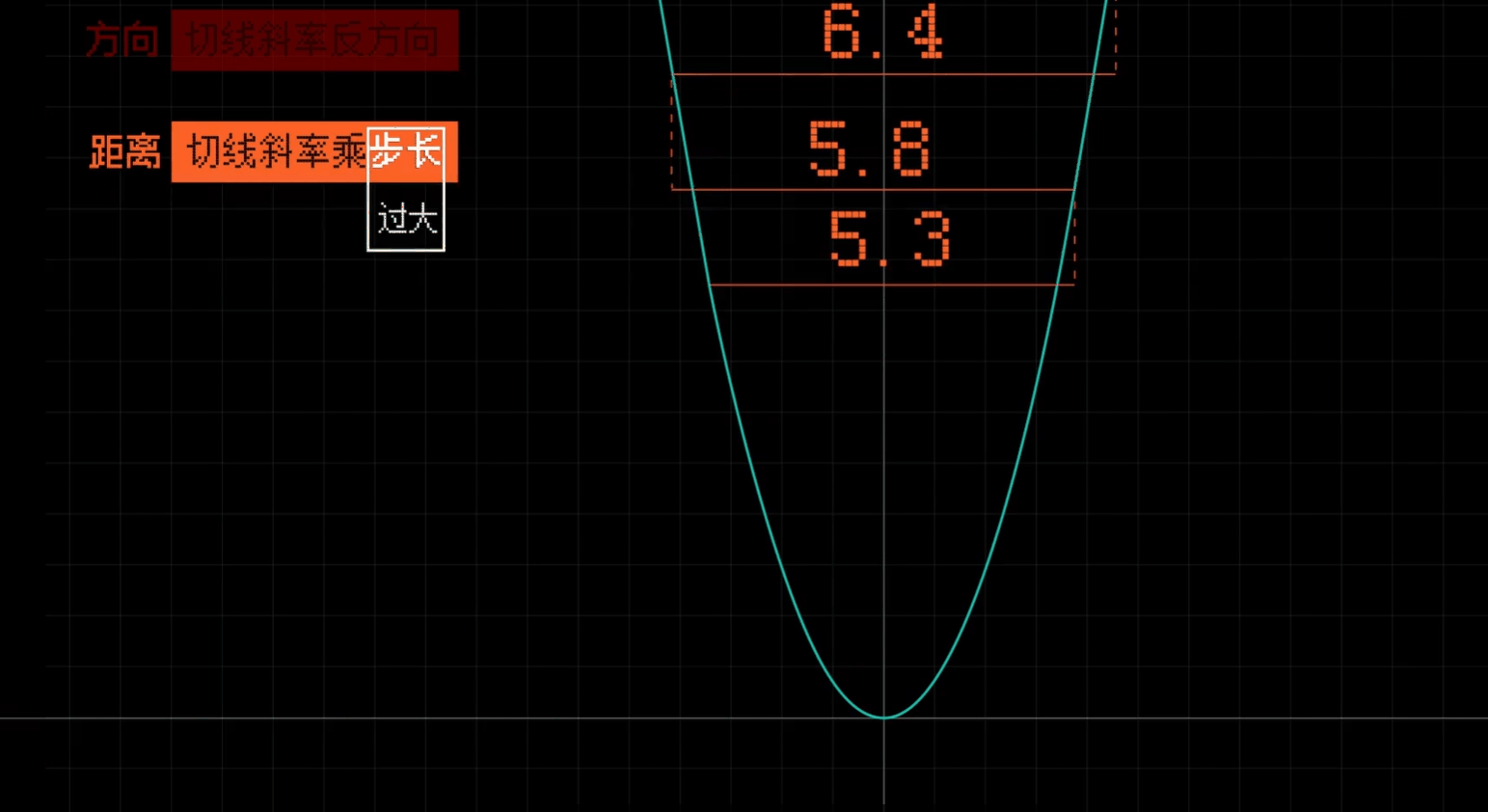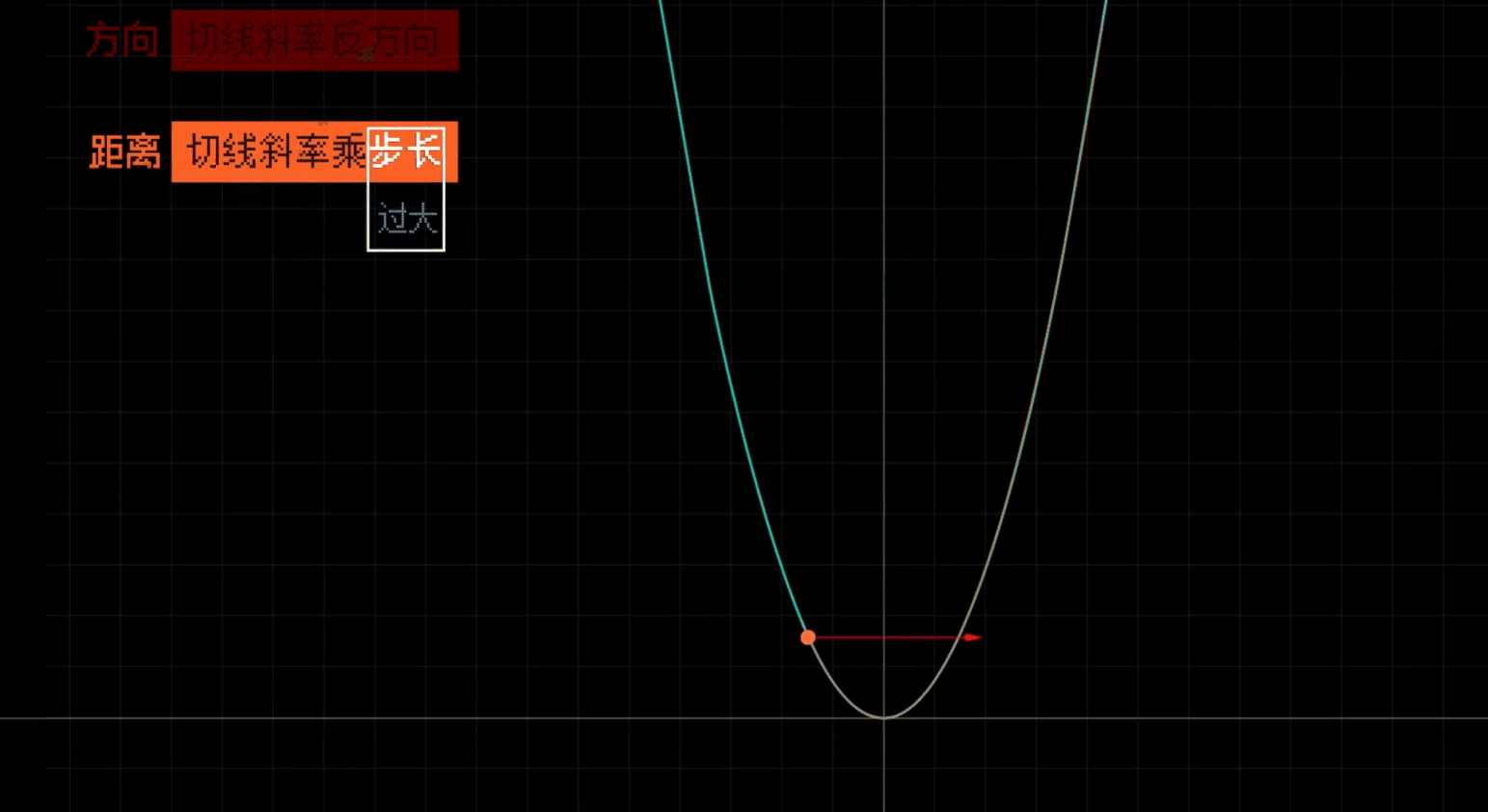
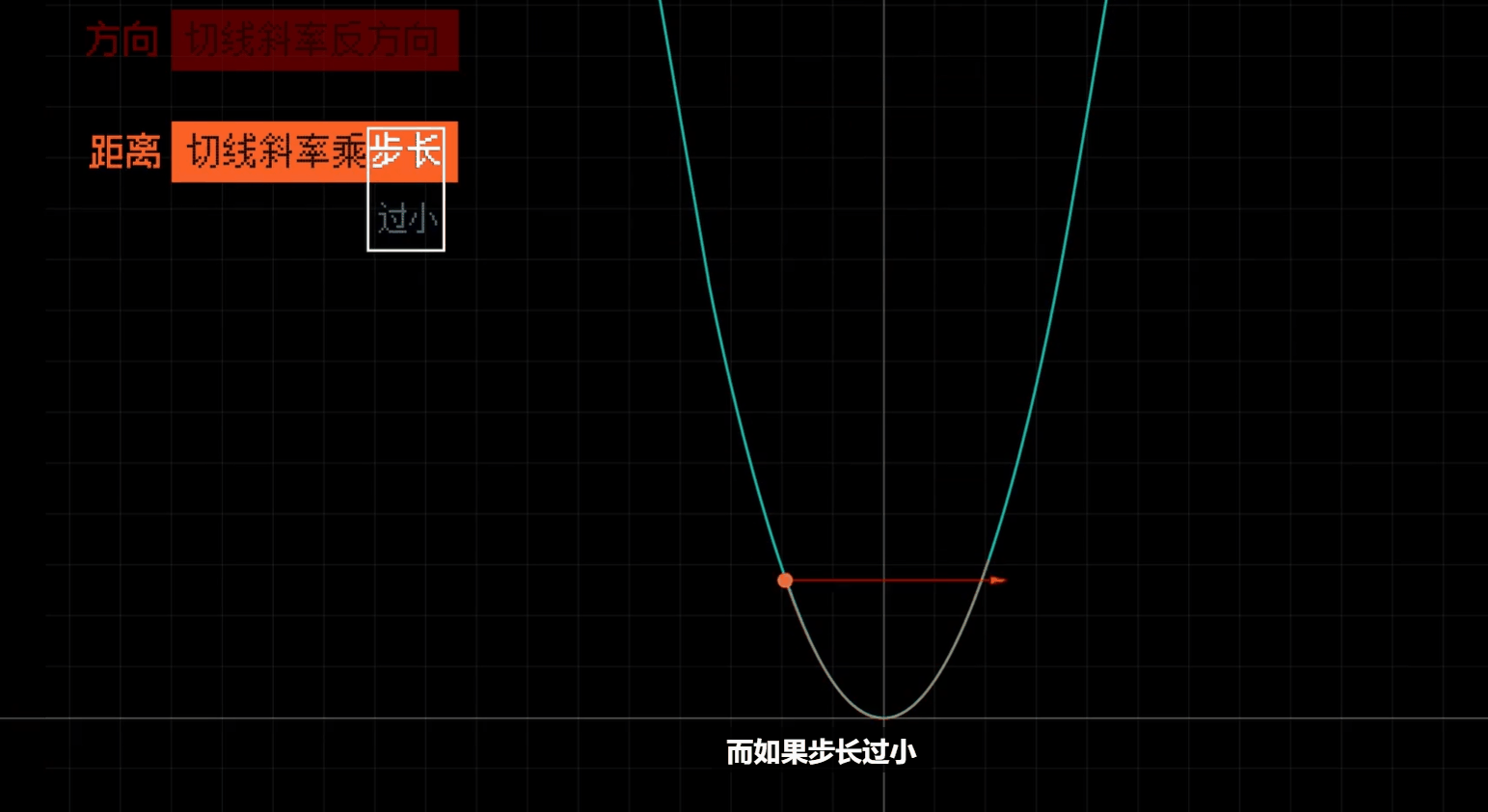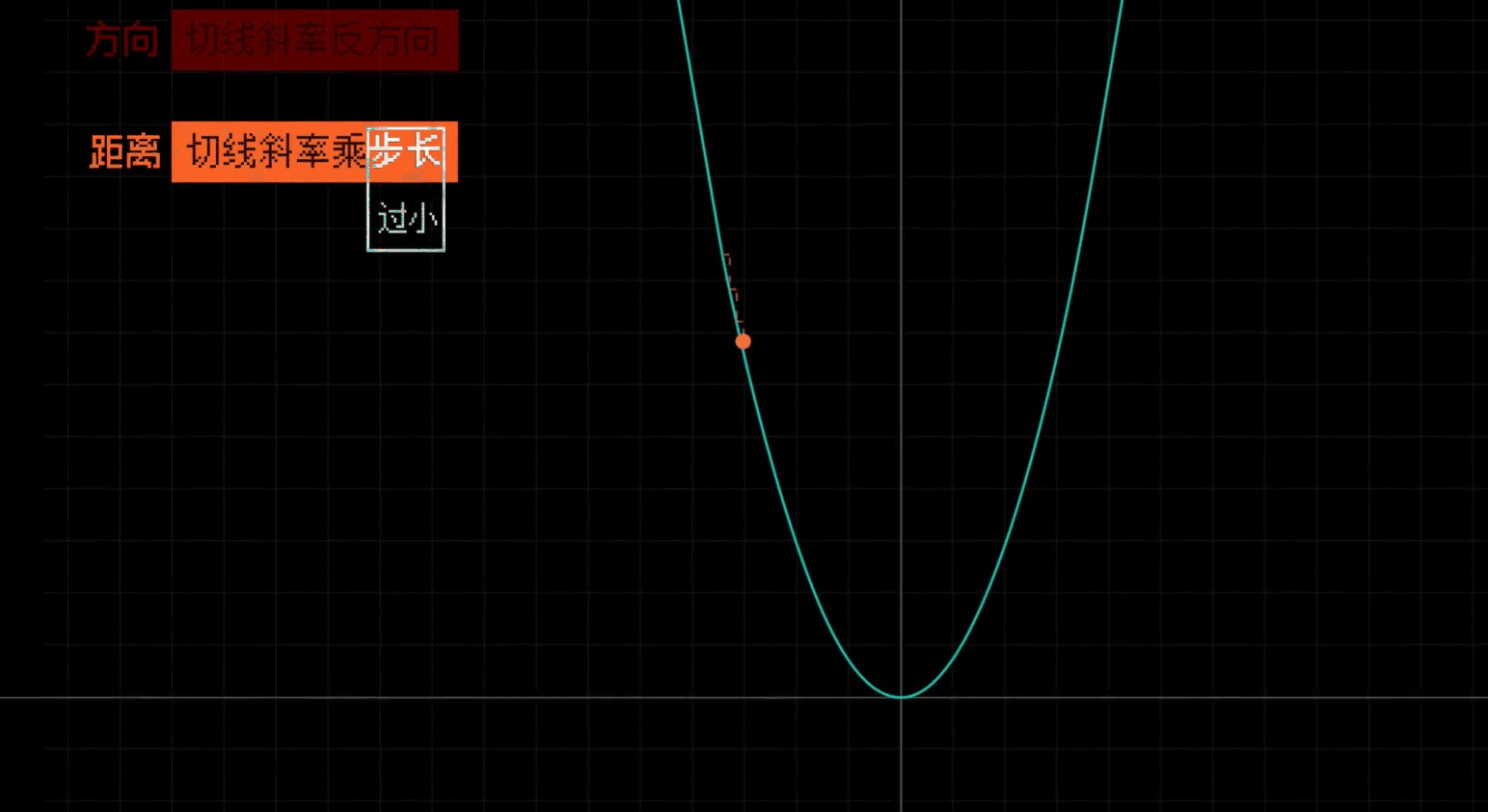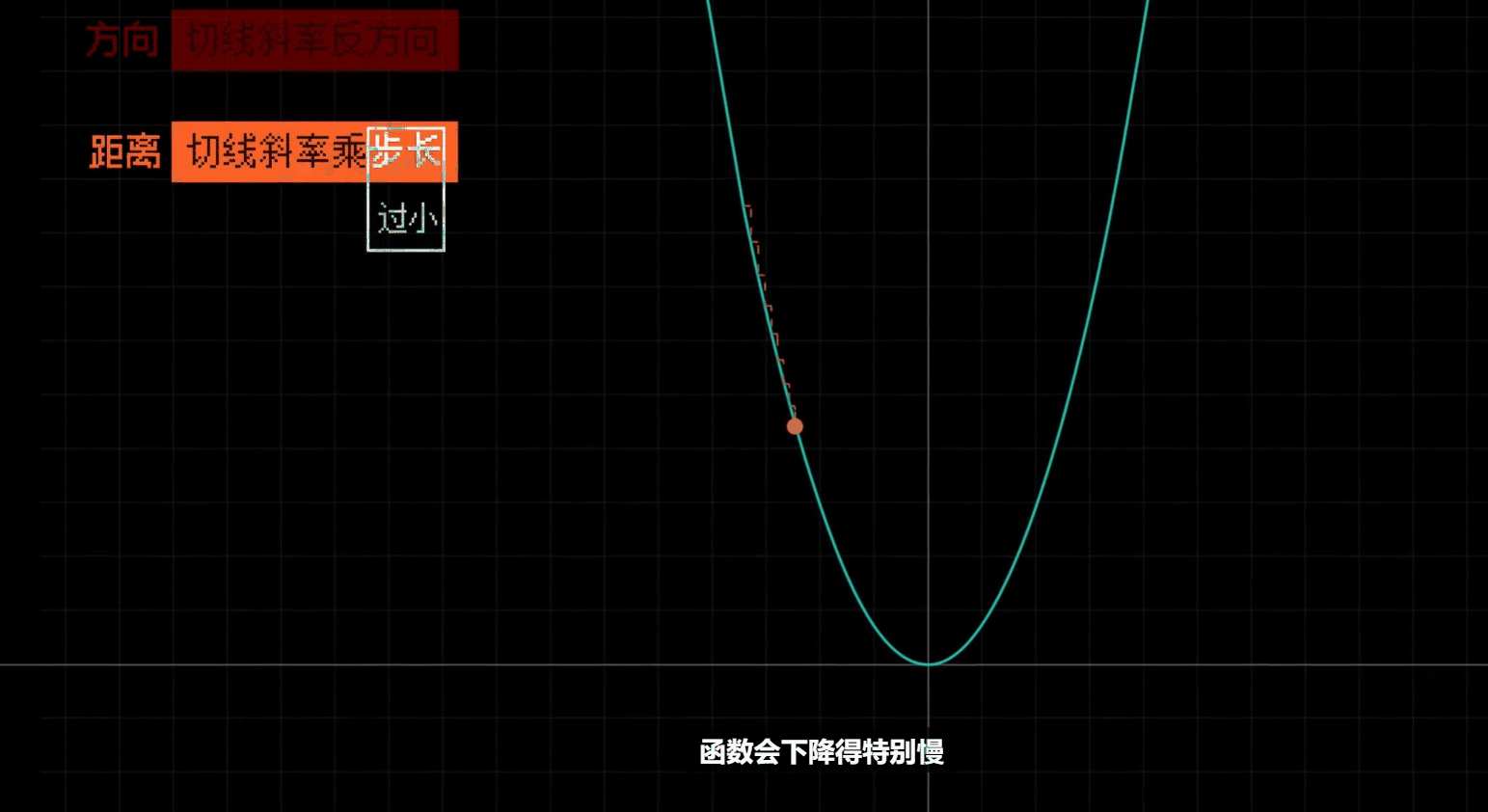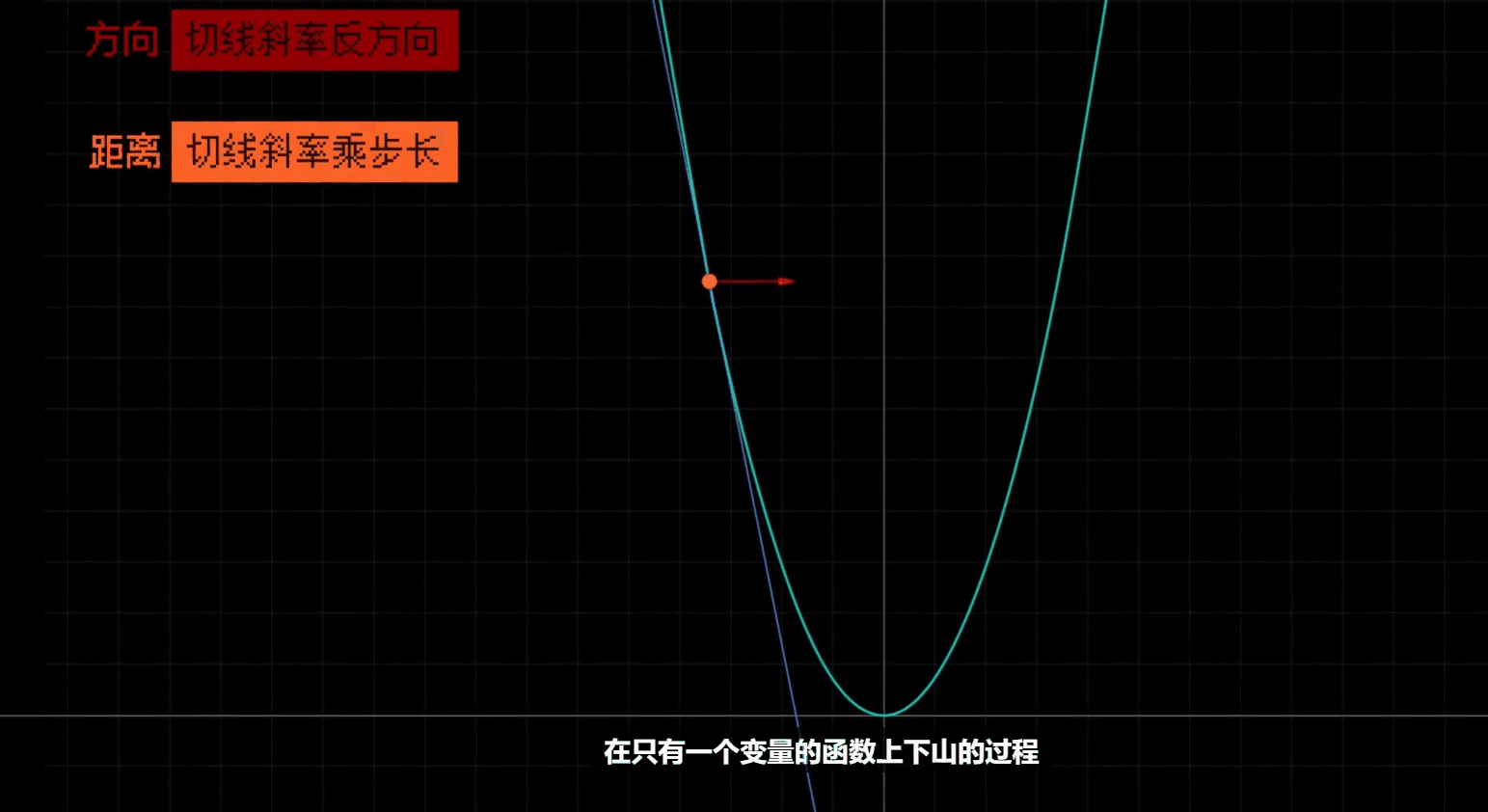
# 需要同时赋值

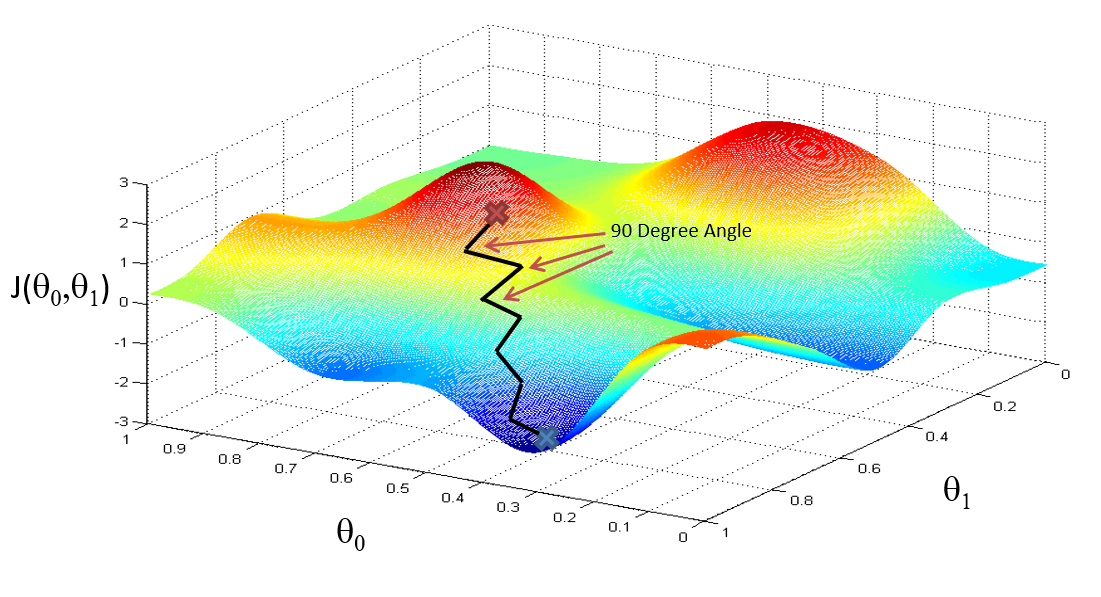
- 这样才能够保证走的方向是梯度最大的方向
- 如果一前一后地赋值, 那么走的路线是这样ZigZag形状的, 可能能够运作, 但显然不是我们想要的运作方式.
# Different Gradient Descent Methods
Different_Gradient_Descent_Methods
Linear Regression & Gradient Descent
Linear_Regression&Gradient_Descent
Relation_Between_Linear_Regression&Gradient_Descent_梯度下降和线性回归的关系
Logistic Regression & Gradient Descent
Part.14_Logistic_Regression&Gradient_Descent(ML_Andrew.Ng.)