Part.7_Feature_Scaling(ML_Andrew.Ng.)
# Feature Scaling
Tags: #MachineLearning #FeatureEngineering
深入阅读的链接: https://sebastianraschka.com/Articles/2014_about_feature_scaling.html
# When to Use
- 在梯度下降的时候, 缩放数据可以让梯度变化更平滑
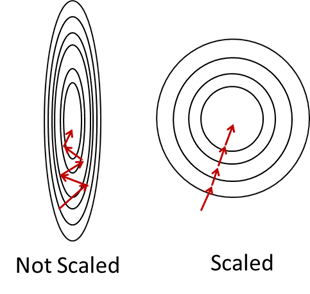
If an algorithm uses gradient descent, then the difference in ranges of features will cause different step sizes for each feature. To ensure that the gradient descent moves smoothly towards the minima and that the steps for gradient descent are updated at the same rate for all the features, we scale the data before feeding it to the model. Having features on a similar scale will help the gradient descent converge more quickly towards the minima.
Specifically, in the case of Neural Networks Algorithms, feature scaling benefits optimization by:
- It makes the training faster
- It prevents the optimization from getting stuck in local optima
- It gives a better error surface shape
- Weight decay and Bayes optimization can be done more conveniently
- 在以距离为基础的算法里面, 放缩数据可以让数据分布更均匀
Distance-based algorithms like KNN, K-means, and SVM are most affected by the range of features. This is because behind the scenes they are using distances between data points to determine their similarity and hence perform the task at hand. Therefore, we scale our data before employing a distance-based algorithm so that all the features contribute equally to the result.
- 在主成分分析里面, 放缩数据可以让凸显出数据的"变化", (一个数量级很大的数据变一点点»一个数量级很小的数据变化几倍)
In PCA we are interested in the components that maximize the variance. If one component (e.g. age) varies less than another (e.g. salary) because of their respective scales, PCA might determine that the direction of maximal variance more closely corresponds with the ‘salary’ axis, if those features are not scaled. As a change in the age of one year can be considered much more important than the change in salary of one euro, this is clearly incorrect.
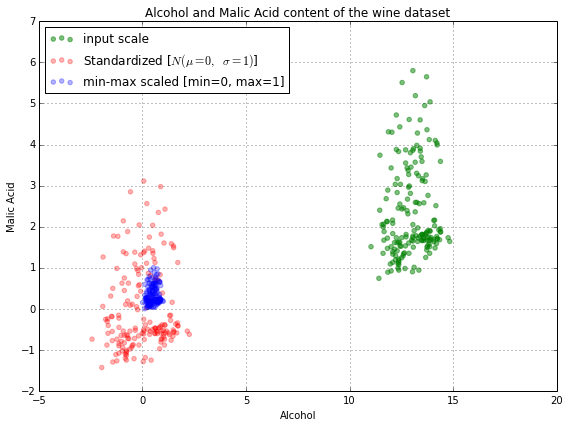
# Normalization 归一化
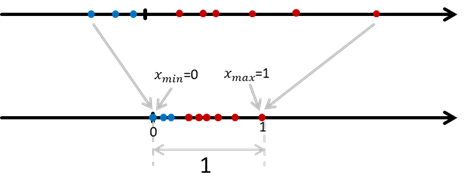
$$x^\prime= \frac{x-x_{min}}{x_{max}-x_{min}}$$
可以自己调控数据分布的范围, 比如你想让数据分布在$[a,b]$范围内, 公式变为: $$x^{\prime}=a+\left(\frac{x-\min (x)}{\max (x)-\min (x)}\right)(b-a)$$
归一化对离群值十分敏感
会缩小很大的数据, 会改变数量级
# Standardization 标准化

- 拿正态分布的数据做例子: 就相当于把其他颜色的曲线都变成红色的那条标准正态曲线
$$x^\prime= \frac{x-\mu}{\sigma}$$ $\mu$是均值, $\sigma$是标准差(方差的平方根)
对离群值不是那么敏感
标准化也改变数量级, 会减去均值
# 如何选择2
Normalization 在数据不符合正态分布的时候比较适用, 像KNN这种对数据分布没有要求的模型更适用于归一化
在神经网络里面常常要求数据分布在0-1之间, 这时候归一化必不可少; 另一个例子是图像处理的时候常常会把数据缩小到一个范围(比如0-255), 在这时标准化更加适用.
Standardization 在数据满足正态分布的时候更加适用, 并且在放缩的时候没有范围限制, (不像归一化可以明确的规定一个范围$[a,b]$)
在聚类中, 标准化在比较不同特征的相似性的时候很好用(why? #todo), 另一个例子是PCA的时候常常用标准化来突出数据分布的差异度, 而不是用归一化把最大的变成一. ^375f2a
- 总之:
- Standardization 适用于正态分布的数据,
- Normalization 适用于非正态分布的数据
- Normalization里面离群值对数据的影响显著
- 不知道怎么办就都试试, 比较哪一个效果最好
# Feature Scaling & Regression
在多项式回归里面, 数据放缩很重要, 因为级数增长很快
# Don’t Confuse Regularization Normalization & Standardization
- Regularization: 正则化
- Normalization: 归一化
- Standardization: 标准化