Part.9_Normal_Equation(ML_Andrew.Ng.)
# Normal Equation
Tags: #MachineLearning #NormalEquation #LinearRegression
- Normal Equation 是解 线性回归(Linear Regression) 问题的一种代数方法.
# Definition
The value of $\theta$ that minimizes $J(\theta)$ can be given in closed form by the equation $$ \theta=\left(X^{T} X\right)^{-1} X^{T} \vec{y} $$
其中 $$ X_{m\times (n+1)}=\left[\begin{array}{c} -\left(x^{(1)}\right)^{T}- \\ -\left(x^{(2)}\right)^{T}- \\ \vdots \\ -\left(x^{(m)}\right)^{T}- \end{array}\right] . $$ (其中$x$是$n+1$维列向量) $$ \vec{y}_{m\times 1}=\left[\begin{array}{c} y^{(1)} \\ y^{(2)} \\ \vdots \\ y^{(m)} \end{array}\right] . $$
# Intuitive
- 这实际上是在求$X$矩阵列空间:$\mathrm{Col}(X)$中, 最接近向量$\vec{y}$的向量$X\vec\theta$(投影$\mathrm{proj}_{\mathrm{Col(}X\mathrm )}(\space \vec y\space )$1), 这里$\theta$可以看作是这个投影在列空间里面的坐标.
- 这里的列向量就是所有样本里面的每一个单独的Feature构成的向量.
- 这样看来, 问题的求解就是要在特征构成的"特征空间"里面找到一个点, 这个点最接近真实值$\vec y$ (这其实是
Linear Regression的Intuition, Normal Equation方法促使我用线性代数的角度来看待这个问题)
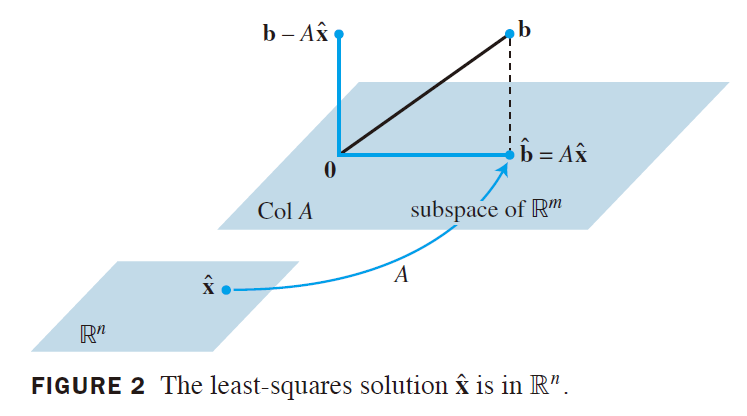 2
上图是__线性代数及其应用__此书里面一个形象的图例, 参数$\hat x / \theta$的维数与特征数相同(n或者n+1), 而每一个特征的"长度"是样本数m, 真实值的数量也是m
2
上图是__线性代数及其应用__此书里面一个形象的图例, 参数$\hat x / \theta$的维数与特征数相同(n或者n+1), 而每一个特征的"长度"是样本数m, 真实值的数量也是m - 注意列空间的维数很可能不是$m$, 但是真实值向量$\vec y$是在$\mathbb R_m$里面取的, 所以我们常常需要求一个近似解$X\vec\theta$
- 如果列空间的维数就是m, 那么我们能够把损失函数降为0, 即拟合曲线经过所有样本点. 3
具体的数学知识参见Linear Algebra and Its Applications by David C. Lay 第6章
# 推导
假设要得到$\theta$, 使$X\theta$尽可能靠近$\vec y$
# 通过向量空间推导
详细推导见上方提及的书Linear Algebra and Its Applications by David C. Lay 第6章
大概思路: $X$ 的列向量垂直于$(\vec y -\mathrm {proj}_{Col(X)}\space \vec y)=(\vec y-X\theta)$, 所以$X$的列与$(\vec y-X\theta)$的内积为0, 也就相当于$X^T$与$(\vec y-X\theta)$的矩阵积为0 $\Rightarrow X^T(\vec y-X\theta)=0 \Rightarrow X^T\vec y=X^TX\theta$
然后如果$X$的列向量独立, 那么$X^TX$可逆, 那么$\theta=(X^TX)^{-1}X^T\vec y$
# 求导数
Normal_Equation_Proof_2_Matrix_Method
# 局限性
首先, 正规方程法做的只是尽可能地让拟合的曲线与样本点的差别最小, 即使曲线通过所有的样本点也不代表模型的预测效果很好, 因为还要考虑模型选取的合理性(曲线还是直线, etc), 数据里面的噪声等等因素. 这样看来正规方程法其实只是一种解方程的方法.
Normal Equation方法解决的问题都具有这样的形式: $$y=X\beta+\varepsilon$$(其中$\varepsilon$是余差向量, 相当于预测值与真实值的误差), 这样的方程称为线性模型.4
线性模型可以进行直线拟合也可以进行曲线拟合, 所求的最优解都是最小二乘拟合.
- 曲线的一个例子:
$$ \begin{aligned} &\left[\begin{array}{c} y_{1} \\ y_{2} \\ \vdots \\ y_{n} \end{array}\right]=\left[\begin{array}{ccc} 1 & x_{1} & x_{1}^{2} \\ 1 & x_{2} & x_{2}^{2} \\ \vdots & \vdots & \vdots \\ 1 & x_{n} & x_{n}^{2} \end{array}\right]\left[\begin{array}{c} \beta_{0} \\ \beta_{1} \\ \beta_{2} \end{array}\right]+\left[\begin{array}{c} \varepsilon_{1} \\ \varepsilon_{2} \\ \vdots \\ \varepsilon_{n} \end{array}\right]\\ &\quad y\quad=\quad\quad X \quad \quad\quad \quad \beta\quad+\quad\varepsilon \end{aligned}$$
- 一般的, 一个有两个独立变量$u,v$的线性模型可以用以下方程来预测: $$ y=\beta_{0} f_{0}(u, v)+\beta_{1} f_{1}(u, v)+\cdots+\beta_{k} f_{k}(u, v) $$ 此处, $f_{0}, \cdots, f_{k}$ 是某类已知函数, $\beta_{0}, \cdots, \beta_{k}$ 是未知权值.
# Normal Equation & Noninvertibility
因为方程是$\theta=\left(X^{T} X\right)^{-1} X^{T} \vec{y}$ , 在以下两种情况的时候, 可能会出现$(X^{T} X)$不可逆的情况:
- 有多余的特征 / 特征之间线性相关 $\rightarrow$ 删除多于特征即可
- 特征数目大于样本数目: $n>m$, $\rightarrow$ 删除一些特征或者利用"正则化Regularization"
- Don’t Confuse Regularization Normalization and Standardization
在Octave语言里面 pinv (pseudo inverse) 可以用于求不可逆矩阵的逆 (inv 只能用于可逆矩阵)
# Normal Equation & Gradient Descent
Normal Equation方法只能解决线性回归问题(或者, 更一般地: 多重回归的线性模型4), 相比之下, 梯度下降能解决更多机器学习模型的参数问题
下面是对两个方法的一个比较:
| Gradient Descent | Normal Equation |
|---|---|
| Need to choose alpha | No need to choose alpha |
| Needs many iterations | No need to iterate |
| $O(kn^2)$ | $O(n^3)$, need to calculate inverse of $X^TX$ |
| Works well when n is large | Slow if n is very large |
在正规方程法里面, 计算矩阵的逆的时间复杂度是$\mathcal{O}\left(n^{3}\right) .$ 所以在特征数量很大的时候, 这个方法的速度会很慢. 在实际应用中, 如果n > 10,000 就需要考虑使用梯度下降这种迭代形式来求参数的最优解了.
# 在应用的时候需要注意的地方
在完成作业的时候, 我发现利用Normal Equation 方法和 梯度下降方法所得到的$\theta$值不一样:
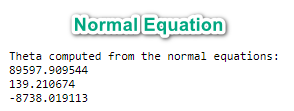
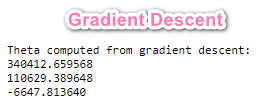
这是因为在梯度下降里面我们运用了Feature Scaling, 而在Normal Equation方法里面, 我们不需要对变量进行放缩.
最后他们的预测结果是完全一样的(考虑误差):

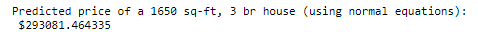
Linear Algebra and Its Applications (4th Edition) by David C. Lay 第6.5节 ↩︎
这时可能有一解或者多解, 联系线性代数里面线性方程组的知识, 如果有多解, 那么说明列向量并不是独立的, 说明特征不是独立的. 具体参见 Linear Algebra and Its Applications (4th Edition) by David C. Lay 第6.5节 ↩︎
Linear Algebra and Its Applications (4th Edition) by David C. Lay 第6.6节, 最小二乘法在线性模型中的应用:
↩︎例4表明,多重回归的线性模型和前面例题中的简单回归模型具有同样的抽象形式,线性代数为我们理解所有线性模型内在的一般原理提供了帮助,定义只要$X$适当,关于$β$的标准方程就具有相同的矩阵形式,不管包含多少变量,这样,对$X^TX$可逆的任何线性模型,最小二乘中的$\hat β$总可由$\left(X^{T} X\right)^{-1} X^{T} \vec{y}$ 计算得到.