Part.23_Forward_Propagation-Neural_Network(ML_Andrew.Ng.)
# Forward Propagation
Tags: #NeuralNetwork #MachineLearning
# Vectorized Implementation
$$\begin{aligned} a_{1}^{(2)} &=g\left(\Theta_{10}^{(1)} x_{0}+\Theta_{11}^{(1)} x_{1}+\Theta_{12}^{(1)} x_{2}+\Theta_{13}^{(1)} x_{3}\right) \\ a_{2}^{(2)} &=g\left(\Theta_{20}^{(1)} x_{0}+\Theta_{21}^{(1)} x_{1}+\Theta_{22}^{(1)} x_{2}+\Theta_{23}^{(1)} x_{3}\right) \\ a_{3}^{(2)} &=g\left(\Theta_{30}^{(1)} x_{0}+\Theta_{31}^{(1)} x_{1}+\Theta_{32}^{(1)} x_{2}+\Theta_{33}^{(1)} x_{3}\right) \\ \end{aligned}$$ 我们把Sigmoid函数里面的部分用$z$代替: $$\begin{aligned} &a_{1}^{(2)}=g\left(z_{1}^{(2)}\right) \\ &a_{2}^{(2)}=g\left(z_{2}^{(2)}\right) \\ &a_{3}^{(2)}=g\left(z_{3}^{(2)}\right) \end{aligned}$$ 同时: $$\begin{aligned} &X = \left[\begin{array}{cccc} x_0 \x_1 \x_2 \x_3 \\ \end{array}\right] =a^{(1)} \end{aligned}$$
第一步变为: $$\begin{aligned} \Theta^{(1)}X =Z^{(1)}= \left[\begin{array}{cccc} z_1^{(2)} \z_2^{(2)} \z_3^{(2)} \\ \end{array}\right] \end{aligned}$$
带入Sigmoid函数得到第二层activation units的输出值:
$$\begin{aligned}
A^{(1)}= Sigmoid(\left[\begin{array}{cccc}
z_1^{(2)} \z_2^{(2)} \z_3^{(2)} \\ \end{array}\right]) = \left[\begin{array}{cccc}
a_1^{(2)} \a_2^{(2)} \a_3^{(2)} \\ \end{array}\right]
\end{aligned}$$
同时加上Bias Unit.
下一层重复上述步骤, 直到得到最终的结果
前向传播是从输入开始, 逐步向前, 利用权重计算输出的过程.
总览:
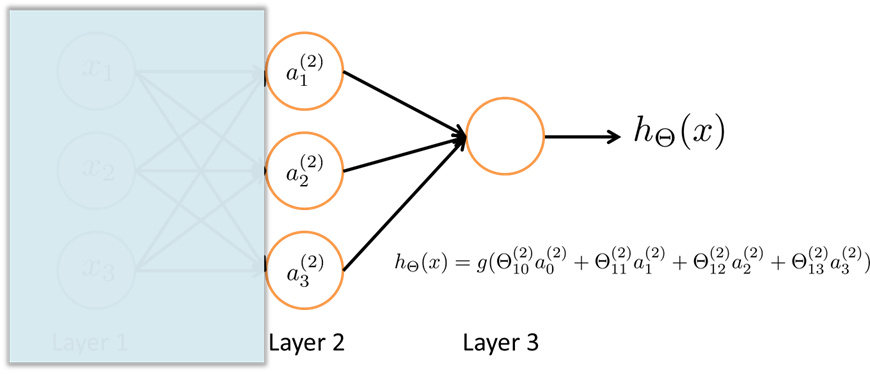
# 与Logistic Regression的联系
在最后一步的时候, 我们进行的操作其实和Logistic Regression一模一样, 每一个Activation Unit的计算过程都可以理解为一次Logistic Regression.