Part.27_Locally_Weighted_Linear_Regression(ML_Andrew.Ng.)

Last updated Sep 30, 2021 Edit Source

• All
• Machine learning
• Linear regression

Tags: #MachineLearning #LinearRegression

Abbreviation: LWR

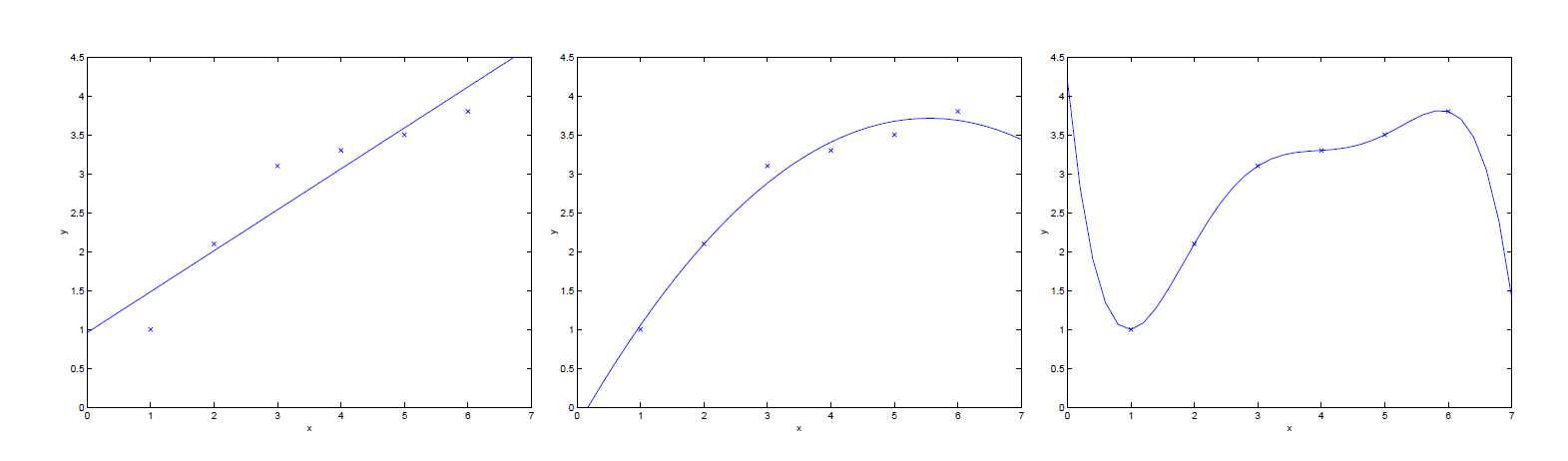
上图展现了Underfitting & Overfitting的情况，而 Locally weighted linear regression (LWR) is an algorithm which, assuming there is sufficient training data, makes the choice of features less critical.

In the original linear regression algorithm, to make a prediction at a query point $x$ (i.e., to evaluate $h(x)$ ), we would:

1. Fit $\theta$ to minimize $\sum_{i}\left(y^{(i)}-\theta^{T} x^{(i)}\right)^{2}$.
2. Output $\theta^{T} x$.

In contrast, the locally weighted linear regression algorithm does the following:

1. Fit $\theta$ to minimize $\sum_{i} w^{(i)}\left(y^{(i)}-\theta^{T} x^{(i)}\right)^{2}$.
2. Output $\theta^{T} x$.

不同:

• 多了一个$w^{(i)}$, 对于每一次query, 我们都需要重新拟合$\theta$

其中$w^{(i)}$的作用是 给最接近这次查询目标$x$的样本点更大的权重(样本越接近查询目标, 那么就可能和查询目标"更像")

一个常用的$w^{(i)}$是:

$$w^{(i)}=\exp \left(-\frac{\left(x^{(i)}-x\right)^{2}}{2 \tau^{2}}\right)$$ 向量形式: $$w^{(i)}= \exp\left(-\frac{(x^{(i)}-x)^{T}(x^{(i)}-x)} {(2 \tau^{2})}\right)$$

因为$w^{(i)}$的指数部分一定是非正的, 考虑指数函数的负半轴部分:

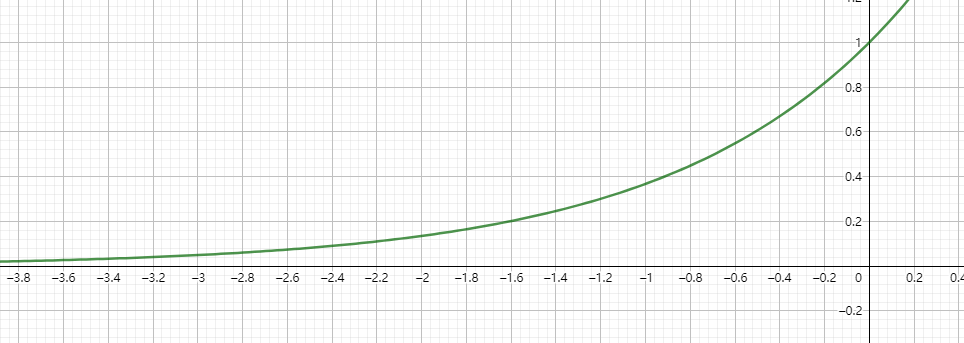
观察发现: $x$越接近$x^{(i)}$, 指数部分越接近$0$, $w^{(i)}$越接近$1$, 这部分特征在损失函数里面的权重越大, 会更着重于让这部分的损失越小, 那么就会更偏重于这部分的参数. 反之, If $w^{(i)}$ is small, then the $\left(y^{(i)}-\theta^{T} x^{(i)}\right)^{2}$ error term will be pretty much ignored in the fit.

bandwidth parameter: The parameter $\tau$ controls how quickly the weight of a training example falls off with distance of its $x^{(i)}$ from the query point $x ; \tau$ is called the bandwidth parameter. (调整"到底距离$x$多远才算重要的样本点")

• 虽然 $w^{(i)}$的这个形式和正态分布很像, 但是其实没有什么联系, 因为 $w^{(i)}$不是随机变量, 也不服从独立同分布.

• LWR是一种非参数算法, 因为这个算法的输出和样本还有紧密的联系:

• Locally weighted linear regression is the first example we’re seeing of a non-parametric algorithm. The (unweighted) linear regression algorithm that we saw earlier is known as a parametric learning algorithm, because it has a fixed, finite number of parameters (the $θ_i$’s), which are fit to the data. Once we’ve fit the $θ_i$’s and stored them away, we no longer need to keep the training data around to make future predictions. In contrast, to make predictions using locally weighted linear regression, we need to keep the entire training set around. The term “non-parametric” (roughly) refers to the fact that the amount of stuff we need to keep in order to represent the hypothesis h grows linearly with the size of the training set.