矩阵的不同乘法-Hadamard-Kronecker

Last updated Feb 1, 2022 Edit Source

• All
• Matrix
• Math

Tags: #Matrix #Math

对应位置的元素相乘 $$ \begin{bmatrix} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33} \end{bmatrix} \circ \begin{bmatrix} b_{11} & b_{12} & b_{13}\\ b_{21} & b_{22} & b_{23}\\ b_{31} & b_{32} & b_{33} \end{bmatrix} = \begin{bmatrix} a_{11}, b_{11} & a_{12}, b_{12} & a_{13}, b_{13}\\ a_{21}, b_{21} & a_{22}, b_{22} & a_{23}, b_{23}\\ a_{31}, b_{31} & a_{32}, b_{32} & a_{33}, b_{33} \end{bmatrix}$$

• Hadamard product 符号表示为: $A \circ B$ or $A \odot B$

• 克罗内克积（英语：Kronecker product）是两个任意大小的矩阵间的运算，表示为$\bigotimes$。克罗内克积是外积从向量到矩阵的推广，也是张量积在标准基下的矩阵表示。
• 类似于外积:
• 
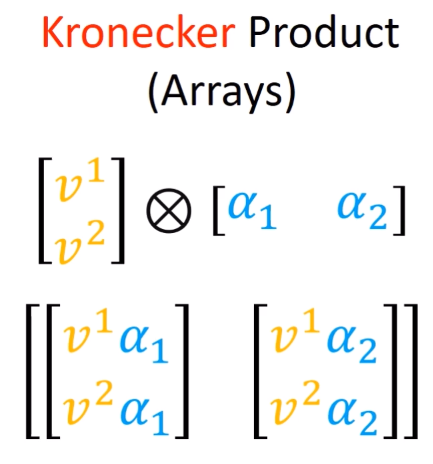
• 对于向量:
  • $$\mathbf{v} = \begin{bmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{bmatrix}$$ 和 $$\mathbf{w} = \begin{bmatrix} w_1 \\ w_2 \\ \vdots \\ w_m \end{bmatrix}$$ their outer product or Kronecker product is given by the $n \times m$ matrix $$\mathbf{v} \otimes \mathbf{w} = \begin{bmatrix} v_1 w_1 && v_1 w_2 && \cdots && v_1 w_m \\ v_2 w_1 && v_2 w_2 && \cdots && v_2 w_m \\ \vdots && \vdots && \ddots && \vdots \\ v_n w_1 && v_n w_2 && \cdots && v_n w_m\end{bmatrix}$$
• 进一步地, 对于 $2 \times 2$ 矩阵 $A$ 和 $3 \times 2$ 矩阵 $B$ 他们的Kronecker Product是$6 \times 4$ 矩阵: $$ \begin{aligned} \mathrm{A} \otimes \mathrm{B} &=\left[\begin{array}{lll} a_{11} \mathrm{~B} & a_{12} \mathrm{~B} \\ a_{21} \mathrm{~B} & a_{22} \mathrm{~B} \end{array}\right] \\ &=\left[\begin{array}{llll} a_{11} b_{11} & a_{11} b_{12} & a_{12} b_{11} & a_{12} b_{12} \\ a_{11} b_{21} & a_{11} b_{22} & a_{12} b_{21} & a_{12} b_{22} \\ a_{11} b_{31} & a_{11} b_{32} & a_{12} b_{31} & a_{12} b_{32} \\ a_{21} b_{11} & a_{21} b_{12} & a_{22} b_{11} & a_{22} b_{12} \\ a_{21} b_{21} & a_{21} b_{22} & a_{22} b_{21} & a_{22} b_{22} \\ a_{21} b_{31} & a_{21} b_{32} & a_{22} b_{31} & a_{22} b_{32} \end{array}\right] \end{aligned} $$

Tensor Product vs Kronecker Product

Tensors for Beginners 13: Tensor Product vs Kronecker Product - YouTube