D2L-1-What_is_a_tensor
# What is a tensor?
2022-01-25
Tags: #Tensor #DeepLearning
最初, 张量是在物理和数学里面的一个概念, 后来深度学习借用了这个名词, 但是意义有所改变.
在数学与物理学的语境里面, “Tensor"是一个抽象的概念, 用于表示在坐标变换下的一种不变量, 比如广义相对论中, 坐标的变换会引起观测的时空的变换。而爱因斯坦张量(Einstein tensor)是广义相对论中用来描述时空曲率的一个张量, 不随坐标的变换而变换.
在深度学习的语境里面, “Tensor"是多维数组的一种表示方式
要理清这其中的关系, 还需要稍微深入的认识一下张量是个什么东西.
# 张量 - 含义一
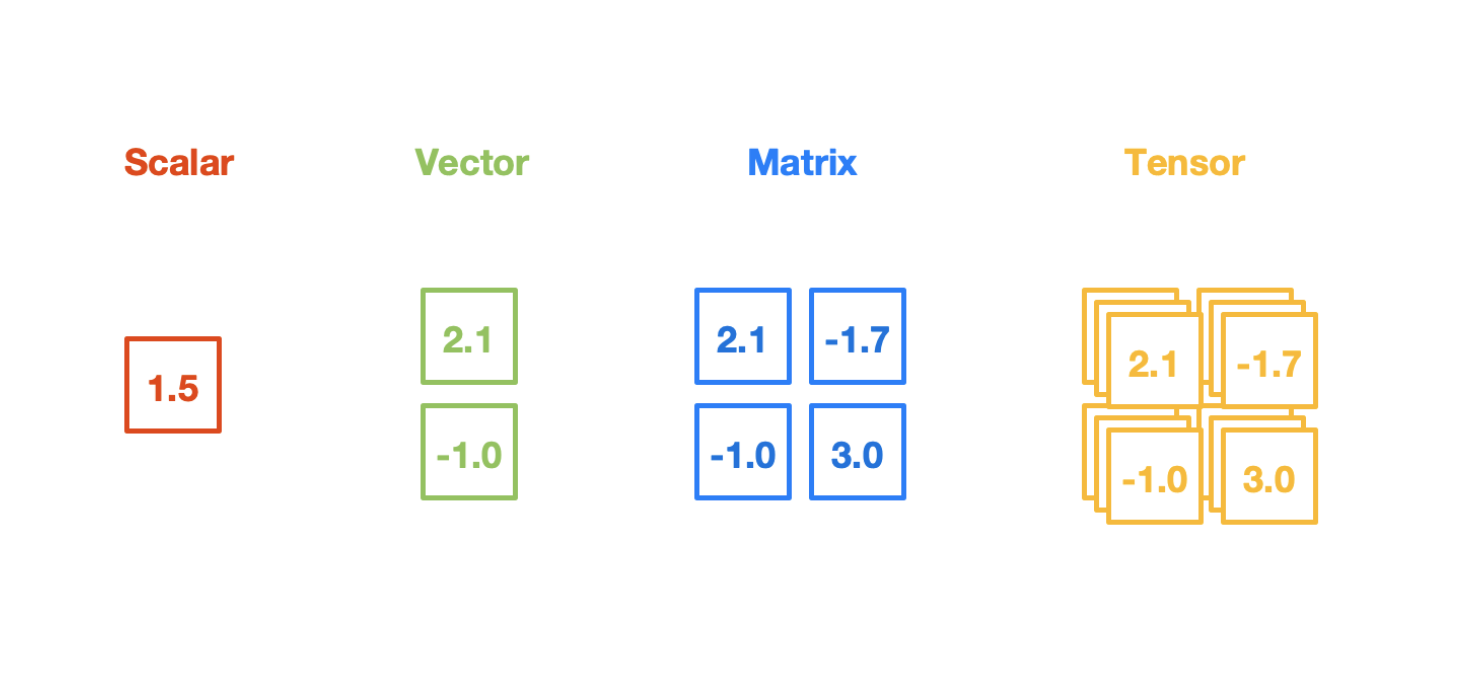
- 在给定坐标系的情况下, 张量可以表示为多维数组的形式. 比如标量(Scalar)就是一个零阶的张量, 向量是一阶的张量, 矩阵是二阶的张量. 在这个含义上, 张量可以看作矩阵的更高阶的推广形式.
- 但是这种定义张量的方式是片面的, 没有表明张量"坐标系变换下的不变性"这一个重要的特征, 后面我们会做简要说明.
# 深度学习里面的张量
搜索了多方资料1, 得知计算机科学里面的"张量"只是 N-d Array 的一种表述方法, 可以看作是矩阵表示法的一种多维推广, 而矩阵只是一种组织数字的二位形式而已.
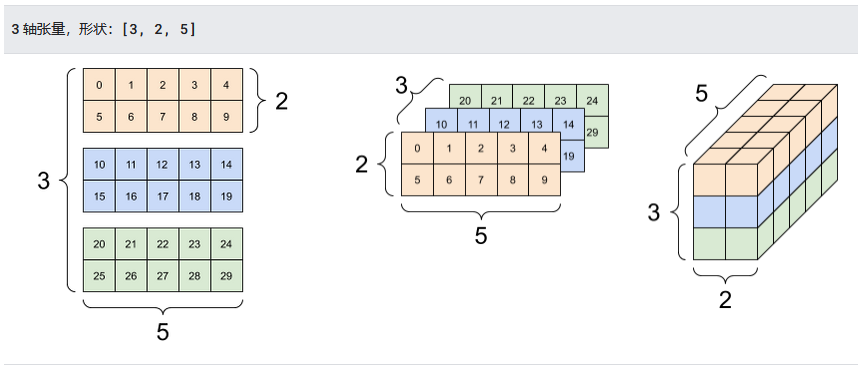
# Tensorflow为什么叫"Tensor"flow
根据Tensorflow给官方教程: 2
张量是具有统一类型(称为
dtype)的多维数组。您可以在tf.dtypes.DType中查看所有支持的dtypes。 如果您熟悉 NumPy,就会知道张量与np.arrays有一定的相似性。
和Wikipedia的介绍: 3
The name TensorFlow derives from the operations that such neural networks perform on multidimensional data arrays, which are referred to as tensors.
所以Tensorflow里面的Tensor其实就是多维数组的意思, 不具备数学定义上张量具备的其他性质.
# 张量: 其他含义
- Youtube上面的博主有一个关于张量的详细介绍4, 里面给出了张量的另外两种定义:
- 考虑定义2. 从一阶张量, 即向量的角度来看, 不变的是坐标系里面的向量自身, 而能够改变的Components是向量的坐标表示, 这个坐标表示根据坐标系的变化而变换, 变化的方式能够用基变换矩阵来刻画.
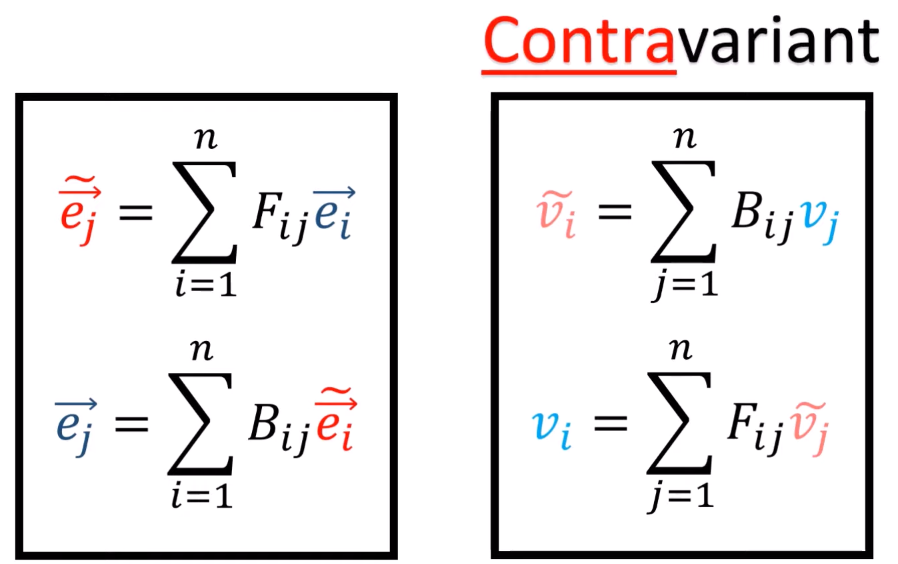
# Covector
Covector在正交基下面就是行向量, 可以看作是一个函数, 这个函数把向量映射成实数(内积).

- Covector的可视化:
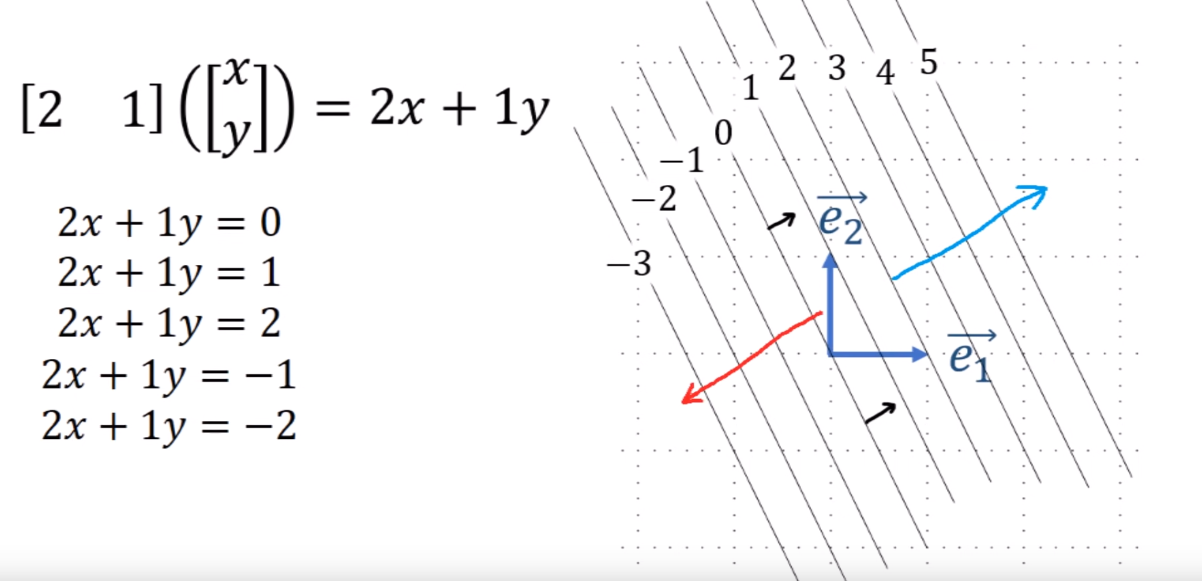
- Covector的变换规则: $\epsilon$是covector的基向量, $\alpha$是covector在$\epsilon$下的坐标


# Tensor Product

- 一个很好的简介:
The Tensor Product, Demystified
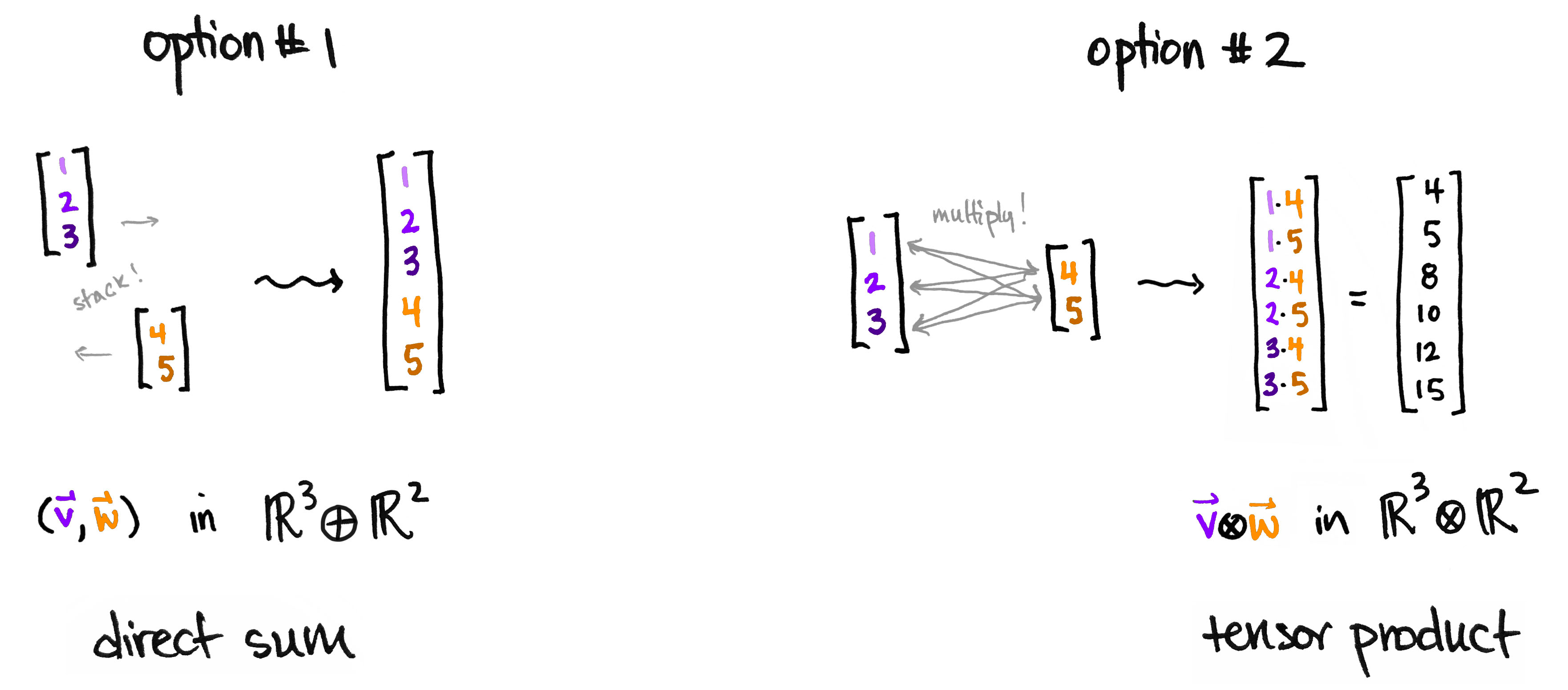
# Linear Map




