D2L-4-矩阵求导
# 矩阵求导
Tags: #Math #Matrix
- 矩阵的求导一直很让人头疼😖
- 之前的笔记: 矩阵的求导
- 李沐这次的讲解方式不太一样,是从标量逐步推广到矩阵,还蛮清晰的。
# 从标量到向量
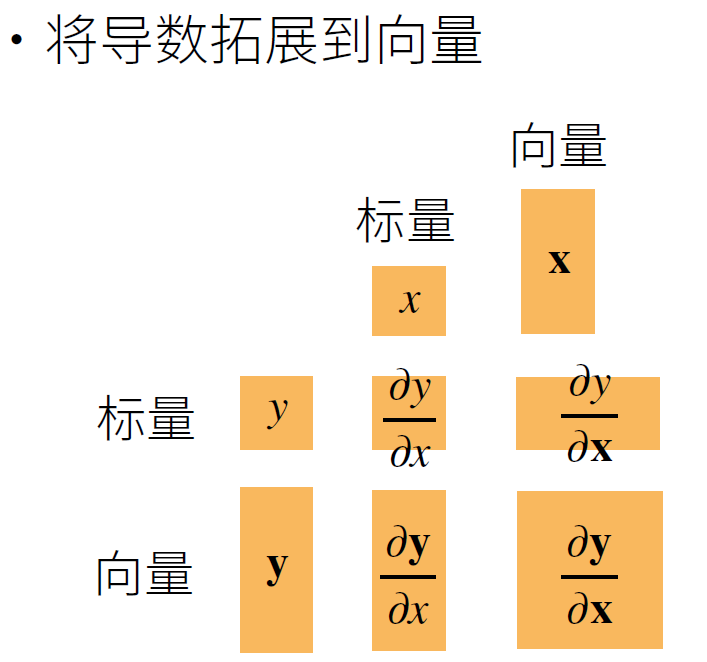 其中 $\Large{\frac{\partial y}{\partial x}, \frac{\partial \mathbf y}{\partial x}}$都很好理解, 尤其需要注意的是当求导的自变量$\mathbf x$为向量的时候, 为
$$\mathbf{x}=\left[\begin{array}{c}
x_{1} \\ x_{2} \\ \vdots \\ x_{n}
\end{array}\right] \quad \frac{\partial y}{\partial \mathbf{x}}=\left[\frac{\partial y}{\partial x_{1}}, \frac{\partial y}{\partial x_{2}}, \ldots, \frac{\partial y}{\partial x_{n}}\right]$$
结果变成了一个行向量.
其中 $\Large{\frac{\partial y}{\partial x}, \frac{\partial \mathbf y}{\partial x}}$都很好理解, 尤其需要注意的是当求导的自变量$\mathbf x$为向量的时候, 为
$$\mathbf{x}=\left[\begin{array}{c}
x_{1} \\ x_{2} \\ \vdots \\ x_{n}
\end{array}\right] \quad \frac{\partial y}{\partial \mathbf{x}}=\left[\frac{\partial y}{\partial x_{1}}, \frac{\partial y}{\partial x_{2}}, \ldots, \frac{\partial y}{\partial x_{n}}\right]$$
结果变成了一个行向量.
# Useful Results
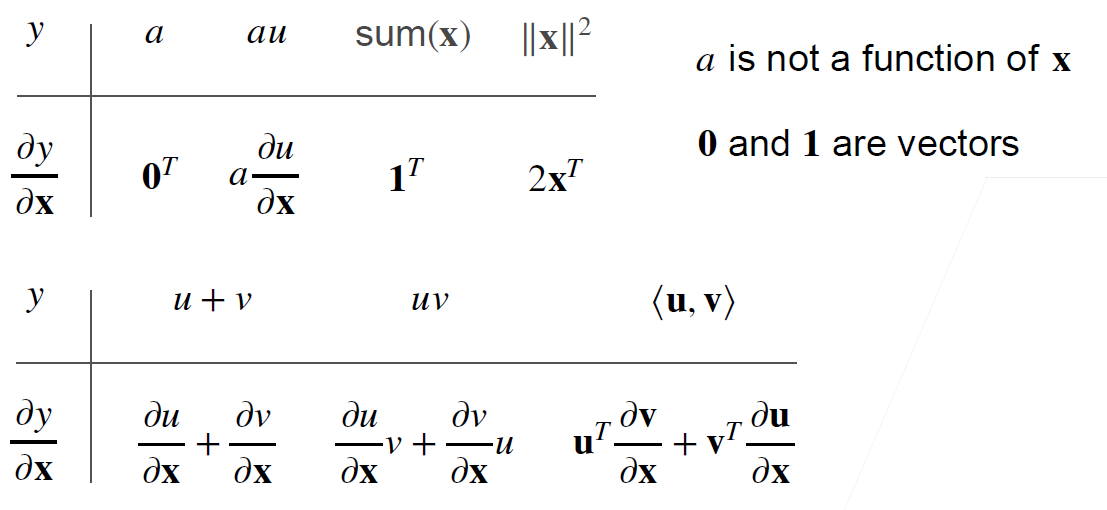
# $\frac{\partial |\mathbf{x}|^2}{\partial \mathbf x}=2\mathbf{x^T}$
$$\mathbf{x}=\left[\begin{array}{c} x_{1} \x_{2} \\vdots \x_{n} \end{array}\right]\quad |\mathbf{x}|^2=\sum^n_1x_i^2$$ $$\begin{aligned} \frac{\partial|\mathbf{x}|^2}{\partial \mathbf{x}}&= \left[\frac{\partial x_i^2}{\partial x_{1}}, \frac{\partial x_i^2}{\partial x_{2}}, \ldots, \frac{\partial x_i^2}{\partial x_{n}}\right]\\ &=\left[2x_1, 2x_{2}, \ldots, 2x_{n}\right]\\ &=2\mathbf{x^T} \end{aligned}$$
# 进一步
而当$\mathbf{x, y}$都是向量的时候, 可以这样理解: $$\begin{aligned} &\mathbf{x}=\left[\begin{array}{c} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \end{array}\right] \quad \mathbf{y}=\left[\begin{array}{c} y_{1} \\ y_{2} \\ \vdots \\ y_{m} \end{array}\right] \\ \end{aligned}$$ $$\frac{\partial \mathbf{y}}{\partial \mathbf{x}}= \left[\begin{array}{c} \frac{\partial y_{1}}{\partial \mathbf{x}} \\ \frac{\partial y_{2}}{\partial \mathbf{x}} \\ \vdots \\ \frac{\partial y_{m}}{\partial \mathbf{x}} \end{array}\right]=\begin{bmatrix} \frac{\partial y_{1}}{\partial x_{1}}& \frac{\partial y_{1}}{\partial x_{2}}& \ldots& \frac{\partial y_{1}}{\partial x_{n}} \\ \frac{\partial y_{2}}{\partial x_{1}}& \frac{\partial y_{2}}{\partial x_{2}}& \ldots& \frac{\partial y_{2}}{\partial x_{n}} \\ &&\vdots \\ \frac{\partial y_{m}}{\partial x_{1}}& \frac{\partial y_{m}}{\partial x_{2}}& \ldots& \frac{\partial y_{m}}{\partial x_{n}} \end{bmatrix}$$
也就是说: $$\mathbf{x} \in \mathbb{R}^{n}, \quad \mathbf{y} \in \mathbb{R}^{m}, \quad \frac{\partial \mathbf{y}}{\partial \mathbf{x}} \in \mathbb{R}^{m \times n}$$
# 直观含义
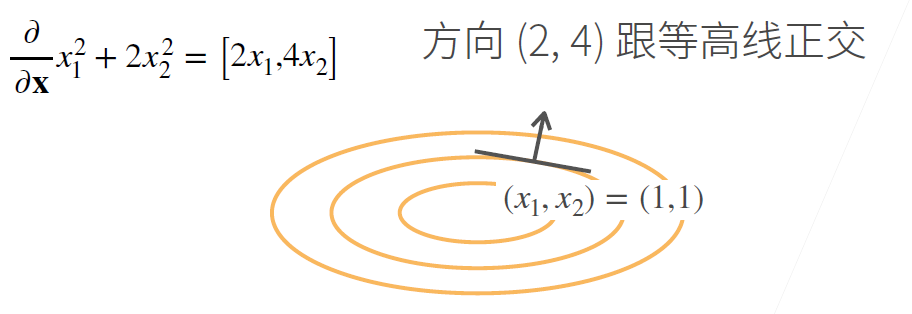 求导后得到梯度向量, 为增长最快的方向
求导后得到梯度向量, 为增长最快的方向
# Useful Results
# $\frac{\partial \mathbf x}{\partial \mathbf x}=I$
$$\frac{\partial \mathbf{x}}{\partial \mathbf{x}}= \begin{bmatrix} \frac{\partial x_{1}}{\partial \mathbf{x}} \\ \frac{\partial x_{2}}{\partial \mathbf{x}} \\ \vdots \\ \frac{\partial x_{m}}{\partial \mathbf{x}} \end{bmatrix}=\begin{bmatrix} \frac{\partial x_{1}}{\partial x_{1}}& \frac{\partial x_{1}}{\partial x_{2}}& \ldots& \frac{\partial x_{1}}{\partial x_{n}} \\ \frac{\partial x_{2}}{\partial x_{1}}& \frac{\partial x_{2}}{\partial x_{2}}& \ldots& \frac{\partial x_{2}}{\partial x_{n}} \\ &&\vdots \\ \frac{\partial x_{m}}{\partial x_{1}}& \frac{\partial x_{m}}{\partial x_{2}}& \ldots& \frac{\partial x_{m}}{\partial x_{n}} \end{bmatrix}= \begin{bmatrix} 1 &0 &\ldots &0 \\ 0 &1 &\ldots &0 \\ \vdots &\vdots&\ddots &\vdots \\ 0 &0 &\ldots &1 \end{bmatrix} $$
# $\frac{\partial \mathbf{Ax}}{\partial \mathbf x}=\mathbf A$
$$\mathbf{x} \in \mathbb{R}^{n}, \quad \mathbf{A} \in \mathbb{R}^{m\times n}$$ 令$\mathbf r_i$代表矩阵$\mathbf A$的行向量, 用 $\langle \mathbf{a} , \mathbf{b} \rangle$表示内积, 第二行为了简化表示, 使用了 Einstein Notation:
$$\begin{aligned}\frac{\partial \mathbf{Ax}}{\partial \mathbf{x}}&= \begin{bmatrix} \frac{\partial \langle r_1 , \mathbf x\rangle}{\partial \mathbf{x}} \\ \frac{\partial \langle r_2 , \mathbf x\rangle}{\partial \mathbf{x}} \\ \vdots \\ \frac{\partial \langle r_m , \mathbf x\rangle}{\partial \mathbf{x}} \\ \end{bmatrix}\&= \large{\begin{bmatrix} \frac{\partial a_{1i}x_i}{\partial x_{1}}& \frac{\partial a_{1i}x_i}{\partial x_{2}}& \ldots& \frac{\partial a_{1i}x_i}{\partial x_{n}} \\ \frac{\partial a_{2i}x_i}{\partial x_{1}}& \frac{\partial a_{2i}x_i}{\partial x_{2}}& \ldots& \frac{\partial a_{2i}x_i}{\partial x_{n}} \\ &&\vdots \\ \frac{\partial a_{mi}x_i}{\partial x_{1}}& \frac{\partial a_{mi}x_i}{\partial x_{2}}& \ldots& \frac{\partial a_{mi}x_i}{\partial x_{n}} \end{bmatrix}}\&= \begin{bmatrix} a_{11} &a_{12} &\ldots &a_{1n} \\ a_{21} &a_{22} &\ldots &a_{2n} \\ \vdots &\vdots&\ddots &\vdots \\ a_{m1} &a_{m2} &\ldots &a_{mn} \end{bmatrix}=\mathbf{A} \end{aligned}$$
# $\frac{\partial \mathbf{x^{T}A}}{\partial \mathbf x}=\mathbf{A^T}$
$$\mathbf{x} \in \mathbb{R}^{n}, \quad \mathbf{A} \in \mathbb{R}^{\color{red}{n\times m}}$$ 令$\mathbf c_i$代表矩阵$\mathbf A$的列向量: $$\begin{aligned}\frac{\partial \mathbf{x^{T}A}}{\partial \mathbf{x}}&= \begin{bmatrix} \frac{\partial \langle c_1 , \mathbf x\rangle}{\partial \mathbf{x}} \\ \frac{\partial \langle c_2 , \mathbf x\rangle}{\partial \mathbf{x}} \\ \vdots \\ \frac{\partial \langle c_n , \mathbf x\rangle}{\partial \mathbf{x}} \\ \end{bmatrix}\&= \large{\begin{bmatrix} \frac{\partial a_{1i}x_i}{\partial x_{1}}& \frac{\partial a_{1i}x_i}{\partial x_{2}}& \ldots& \frac{\partial a_{1i}x_i}{\partial x_{n}} \\ \frac{\partial a_{2i}x_i}{\partial x_{1}}& \frac{\partial a_{2i}x_i}{\partial x_{2}}& \ldots& \frac{\partial a_{2i}x_i}{\partial x_{n}} \\ &&\vdots \\ \frac{\partial a_{mi}x_i}{\partial x_{1}}& \frac{\partial a_{mi}x_i}{\partial x_{2}}& \ldots& \frac{\partial a_{mi}x_i}{\partial x_{n}} \end{bmatrix}}\&= \begin{bmatrix} a_{11} &a_{12} &\ldots &a_{1n} \\ a_{21} &a_{22} &\ldots &a_{2n} \\ \vdots &\vdots&\ddots &\vdots \\ a_{m1} &a_{m2} &\ldots &a_{mn} \end{bmatrix}=\mathbf{A^T} \end{aligned}$$
# 特例: $\frac{\partial \mathbf{x^T}}{\partial \mathbf x}=\mathbf{I}$
$$\frac{\partial \mathbf{x^T}}{\partial \mathbf x}= \frac{\partial\mathbf{x^{T}I}}{\partial \mathbf x}=\mathbf{I^T}=\mathbf{I}$$
# 复合运算
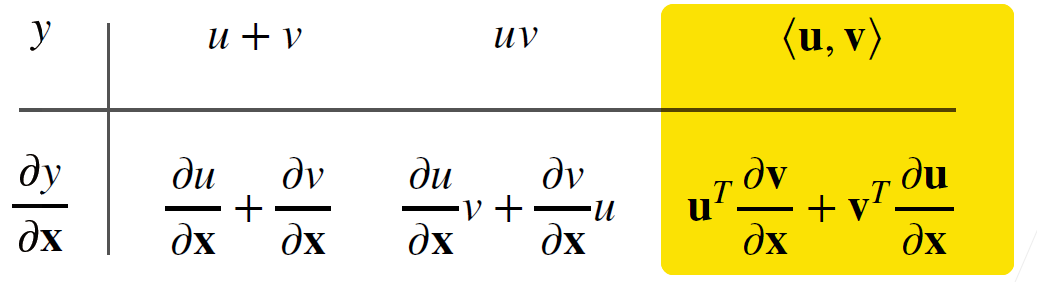
- 需要注意的是$u, v$都是标量, $\mathbf{u,v}$则是向量, 上面可以看出标量相乘的运算律和向量相乘(内积)的运算律是不一样的, 向量内积需要转置, 并且交换位置.
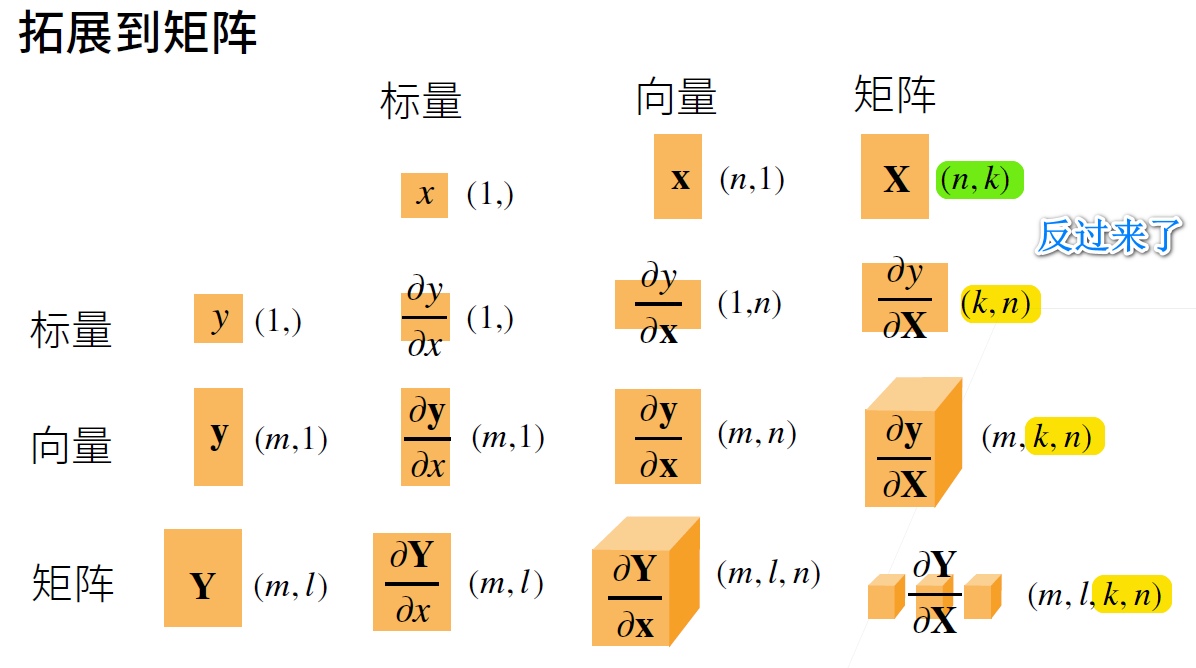
# 从向量到矩阵