D2L-7-自动求导
# 自动求导
2022-02-02
Tags: #DeepLearning
在机器学习里面, 深度学习框架可以帮我们自动求导, 计算梯度.
# 自动求导的两种方式
基于链式法则, 求导有两种顺序:
- 正向累积 $$\frac{\partial y}{\partial x}=\frac{\partial y}{\partial u_{n}}\left(\frac{\partial u_{n}}{\partial u_{n-1}}\left(\ldots\left(\frac{\partial u_{2}}{\partial u_{1}} \frac{\partial u_{1}}{\partial x}\right)\right)\right)$$
- 反向累积、又称反向传递 $$ \frac{\partial y}{\partial x}=\left(\left(\left(\frac{\partial y}{\partial u_{n}} \frac{\partial u_{n}}{\partial u_{n-1}}\right) \ldots\right) \frac{\partial u_{2}}{\partial u_{1}}\right) \frac{\partial u_{1}}{\partial x} $$
# 反向累积/传播
反向传播分为两个阶段: 正向阶段和反向阶段
例子: $$z=(\langle\mathbf{x}, \mathbf{w}\rangle-y)^{2}$$
# 正向阶段
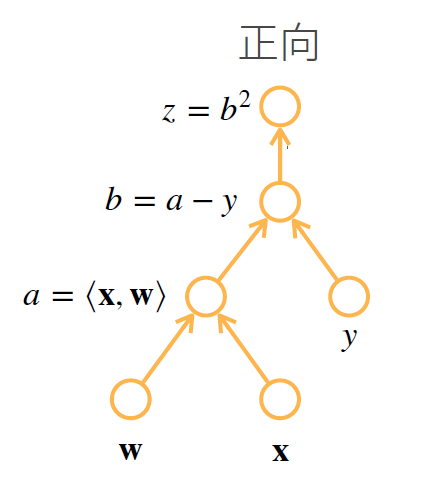根据
计算图, 我们先按照箭头的方向向前计算一次, 并且存储每一步的中间结果. 在反向计算的时候, 我们需要用这些中间结果来计算梯度.
# 反向阶段
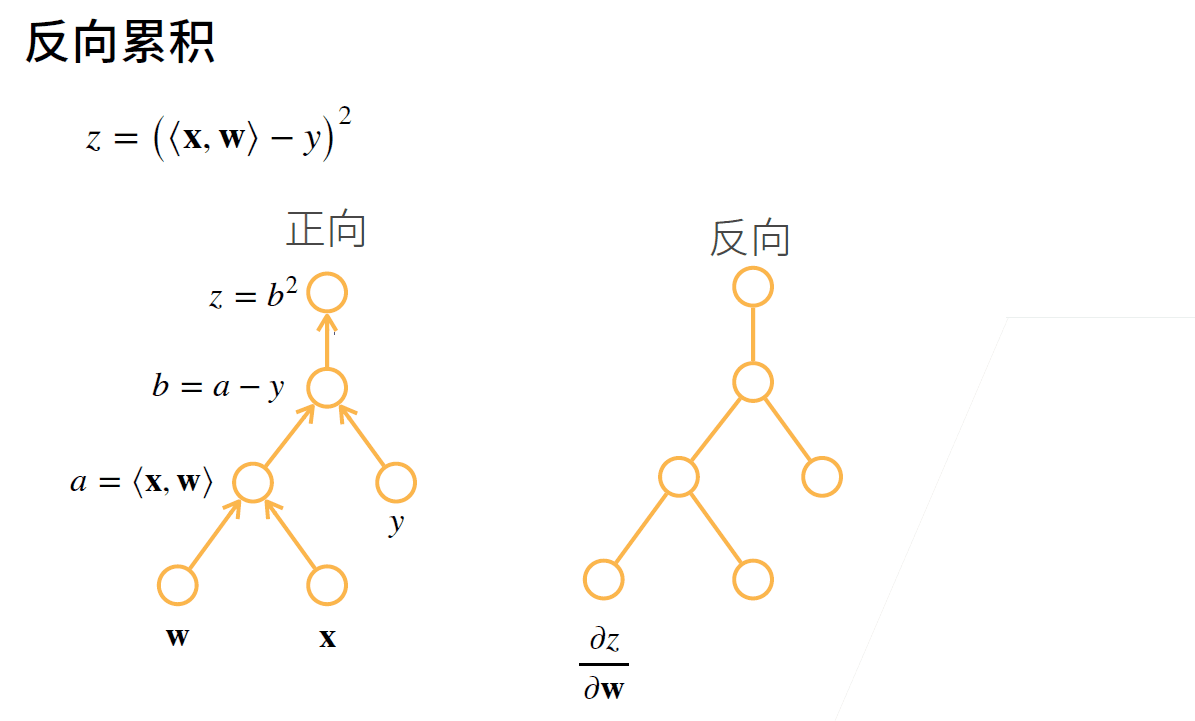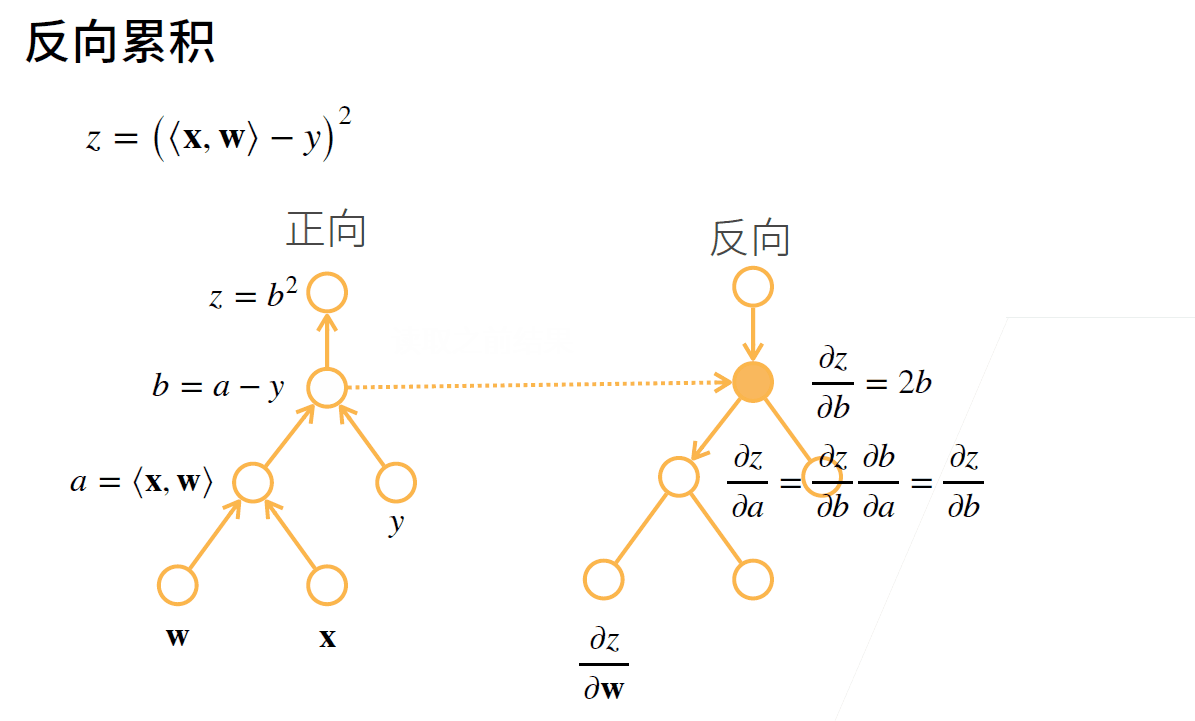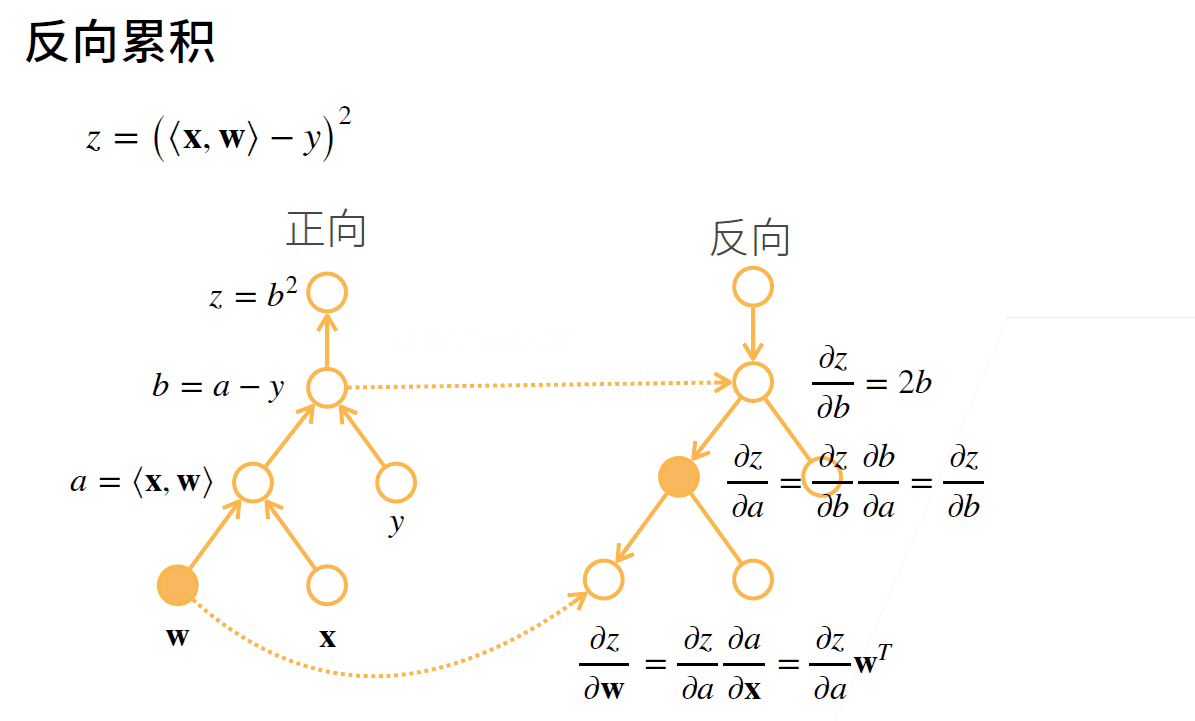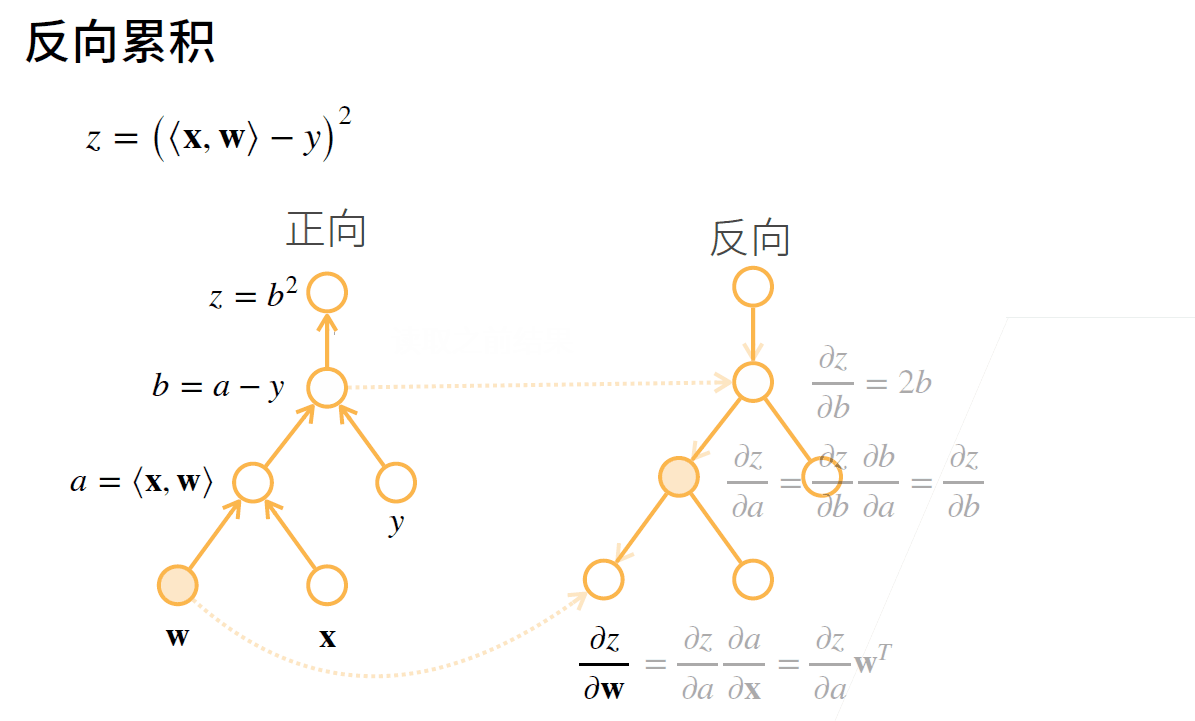反向传播通过不断调用前一步的结果, 从前向后计算每一步的偏导数.