为什么Softmax回归不用MSE
# 为什么Softmax (或者Logistic) 不用MSE作为损失函数?
Tags: #DeepLearning #MachineLearning #SoftmaxRegression #LogisticRegression #CostFunction #MeanSquareError #CrossEntropy
回顾:
- MSE假设样本误差i.i.d., 并且服从正态分布, 最小化MSE等价于极大似然估计. 通常用于回归问题. MSE基于输出与真实值的欧氏距离.
- 最小化Cross Entropy等价于最小化KL散度, 相当于最小化输出概率分布与真实概率分布之间的区别. 通常用于分类问题
在分类问题里面, 我们不使用MSE的原因主要有:
分类问题里面MSE并不是一个凸函数, 这可能会导致算法无法学习到最优的参数.
交叉熵梯度的变化趋势与值域都更理想:
交叉熵的计算更简单.
下面我们依次探究这几点, 由于Logistic回归就是特殊的Softmax回归, 我们先讨论逻辑斯蒂回归, 然后再进一步讨论Softmax.
# Logistic
- 我们先进行公式推导, 然后进行相应的解释.
# 公式推导
对于一个样本 $(\mathbf{x}, y)$ 回忆 Logistic Regression的Hypothesis (我们将偏置直接加到 $\mathbf{w, x}$ 里面): $$h(\mathbf{x})=\operatorname{Sigmoid}(\mathbf{w^T x})$$
损失函数为交叉熵: Part.13_Cost_Function-Logistic_Regression(ML_Andrew.Ng.)] $$L\left(h(\mathbf{x}), y\right)=-y \log \left(h(\mathbf{x})\right)-(1-y) \log \left(1-h(\mathbf{x})\right)$$
- 对其求导 Part.14_Logistic_Regression&Gradient_Descent(ML_Andrew.Ng.) $$\frac{\partial}{\partial w_{j}} L\left(h(\mathbf{x}), y\right) =\left(y-h(\mathbf x)\right) x_{j}$$
- 对其求二阶导: 证明Logistic回归的损失函数是凸函数 $$\frac{\partial^2}{\partial w_{j}^2} L\left(h(\mathbf{x}), y\right) =h(\mathbf x)\left(1-h(\mathbf x)\right) x^2_{j}$$
- 需要注意的是上面都是对于一个样本的情况, 对于多个样本需要加上求和符号
损失函数为MSE: $$L\left(h(\mathbf{x}), y\right)=\frac 1 2(y-h(\mathbf{x}))^2$$
- 对其求导: $$\begin{aligned}\frac{\partial}{\partial w_{j}} L\left(h(\mathbf{x}), y\right)&=-(y-h(\mathbf{x}))\frac{\partial \operatorname{Sigmoid}(\mathbf{w^T x})}{\partial w_{j}}\\ &=-(y-h(\mathbf{x}))h’(\mathbf{x})\frac{\partial\mathbf{w^T x}}{\partial w_{j}}\\ &=-(y-h(\mathbf{x}))h’(\mathbf{x})x_{j}\\ \text{(变成预测值的函数)}&=-(y-h(\mathbf{x}))(1-h(\mathbf{x}))h(\mathbf{x})x_{j} \end{aligned}$$
- 求二阶导数(过程略): $$\begin{aligned}\frac{\partial^2}{\partial w_{j}^2} L\left(h(\mathbf{x}), y\right)&=-\left(3\cdot h^2(\mathbf{x})-2\cdot h(\mathbf{x}) -2y\cdot h(\mathbf{x})+y\right)h’(\mathbf{x})(x_j)^2 \end{aligned}$$
# 解释
- 可视化的函数页面:
Cross Entropy Loss and MSE – GeoGebra
- 注: 这个例子假设有三个样本: $(a,1);(b,1);(c,0)$, 其中输入: $abc$ 都是可以调节的
# 分类问题里面MSE并不是一个凸函数, 这可能导致算法无法学习到最优的参数.
我们作出MSE的二阶导函数图像如下:
 可以看到并不是恒为非负的, 这说明函数并不是凸函数.
可以看到并不是恒为非负的, 这说明函数并不是凸函数.
- 而交叉熵的二阶导图像为:
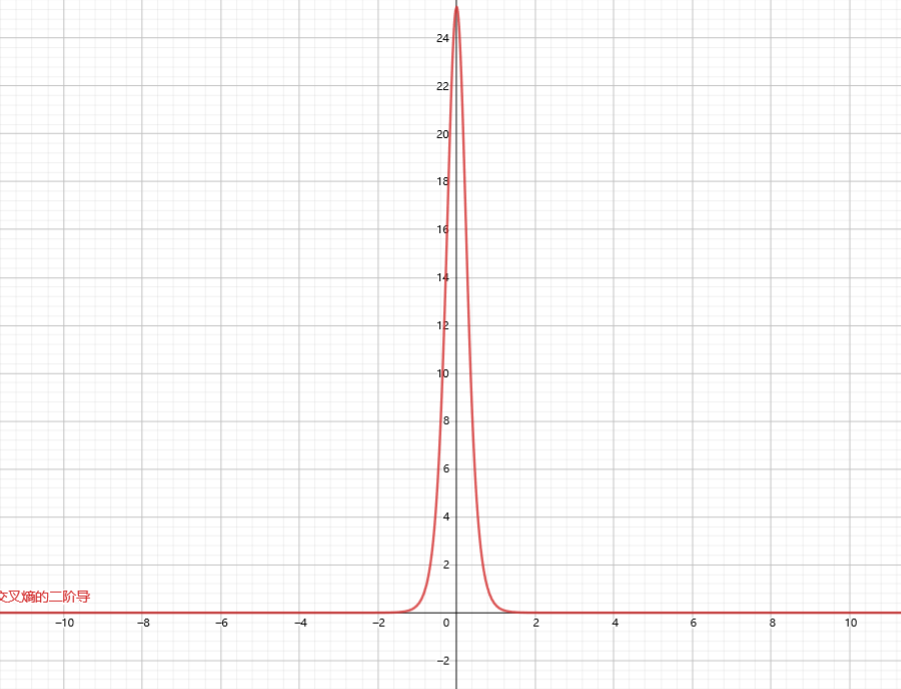
- 这是一个凸函数: 详细证明见: 证明Logistic回归的损失函数是凸函数
# 交叉熵梯度的变化趋势与值域都更理想
值域: 相比均方误差,交叉熵的梯度大小更均匀, 而MSE梯度过小且不够均匀, 容易出现梯度消失的问题.
下图是原函数的图像. 可以看到交叉熵的坡度很"平稳", 梯度下降能够愉快地滑到最低值.
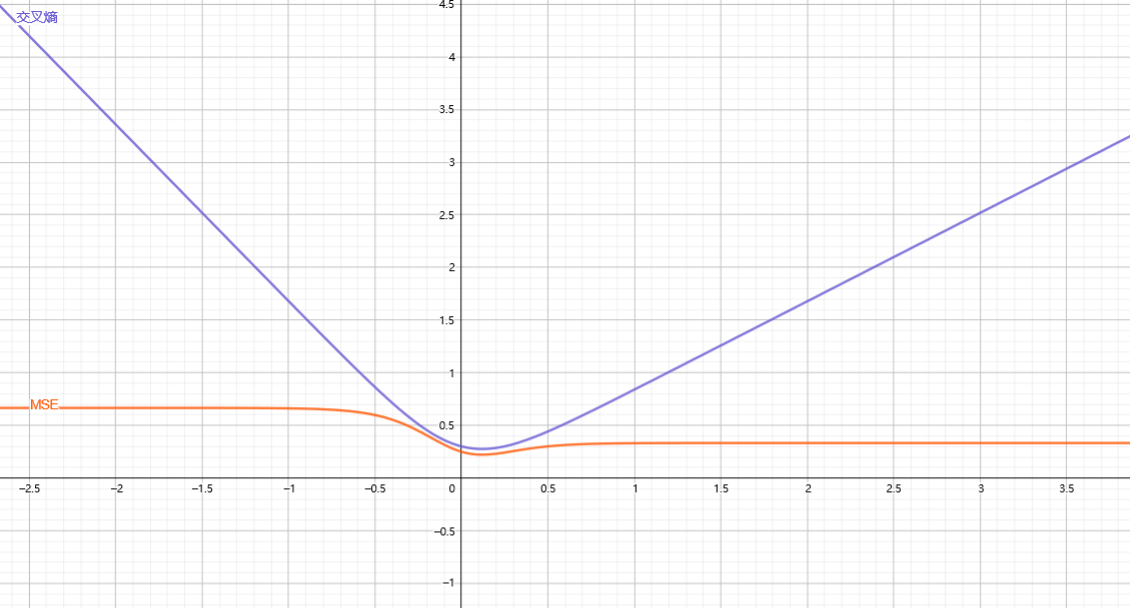
我们再做出其梯度图像:
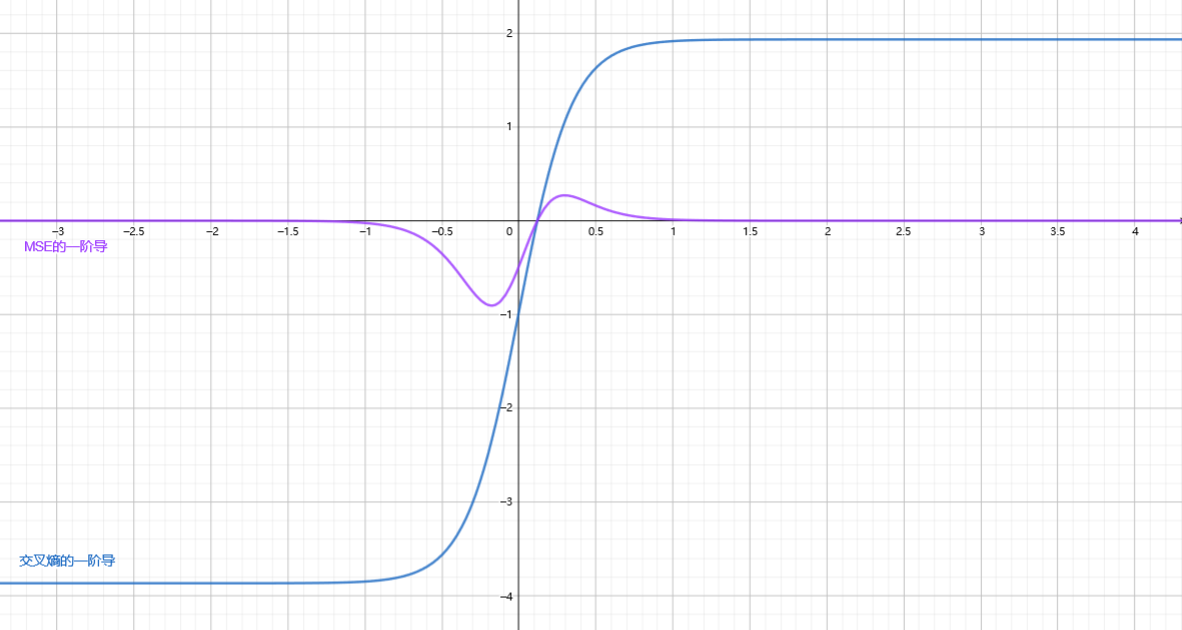
我们发现: MSE的梯度不仅范围小, 而且值的变化还很反常, 在距离最优值(梯度零点)很远的地方反而变得很小.
- 这导致的后果是: 如果参数初始化在距离最优值很远的地方, 训练没有进展.
我们再从数学上分析一下其中的原因:
- 交叉熵的一阶导数为: $$\frac{\partial}{\partial w_{j}}L\left(h(\mathbf{x}), y\right)=\left(y-h(\mathbf x)\right) x_{j}$$
- MSE的一阶导数为: $$\frac{\partial}{\partial w_{j}} L\left(h(\mathbf{x}), y\right)=(y-h(\mathbf{x}))h’(\mathbf{x})x_{j}$$
- MSE的梯度表达式里面多了一项Sigmoid函数的导数, 而Sigmoid函数的导数长下面这个样子(红色虚线):
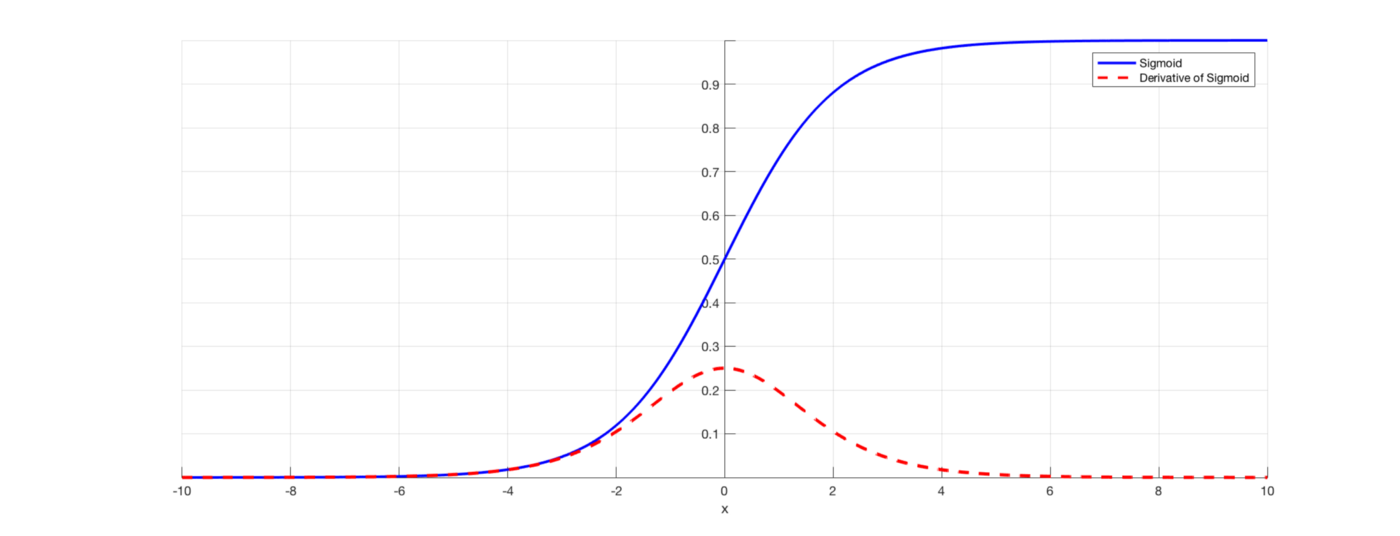 可以看到在绝对值较大的地方, Sigmoid的导数会变得很小, 这也是MSE梯度不理想的原因.
可以看到在绝对值较大的地方, Sigmoid的导数会变得很小, 这也是MSE梯度不理想的原因.
(来自一篇博客1) ….Finally, it reminds me of something said in DL-book by Bengio, ‘You must have some log form loss to cancel the exponential part when your output is sigmoid’
- 如果你网络的最后一层是Sigmoid, 那么你的损失函数需要一些 $\log$ 的部分来抵消掉(Sigmoid里面的)指数部分.
# 交叉熵的计算更简单
- 这是因为:
- 交叉熵的一阶导数为: $$\frac{\partial}{\partial w_{j}}L\left(h(\mathbf{x}), y\right)=\left(y-h(\mathbf x)\right) x_{j}$$
- MSE的一阶导数为: $$\frac{\partial}{\partial w_{j}} L\left(h(\mathbf{x}), y\right)=(y-h(\mathbf{x}))h’(\mathbf{x})x_{j}$$
- 很明显交叉熵少了一个 $h’(\mathbf{x})$
# 另注
在有些解说里面, 作者做出的图像是损失函数关于模型输出的曲线, 我认为这虽然有一定道理, 但也是不太合理的:
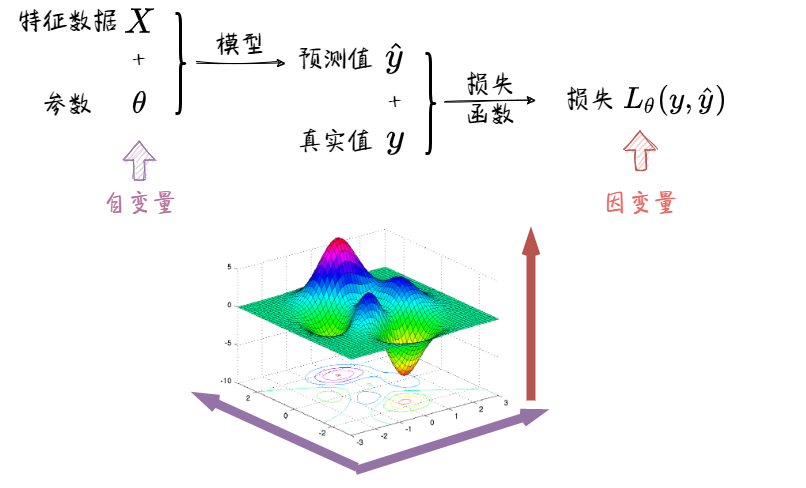
- 我们可以看到要得到损失与参数的关系, 不仅需要经过损失函数, 还需要经过模型, 而模型并不一定是线性的. 所以"预测值-损失"图像并不能真实地反映损失函数是如何影响梯度的大小与变化速度, 进而影响参数更新过程的.
举个例子: 下图展示了真实值 $y=1$ 时, 梯度 $\frac{\partial}{\partial w_{j}} L\left(h(\mathbf{x}), y\right)$ 相对于模型预测值 $h(\mathbf{x})$ 的变化图像:
- 蓝色为交叉熵, 绿色为MSE
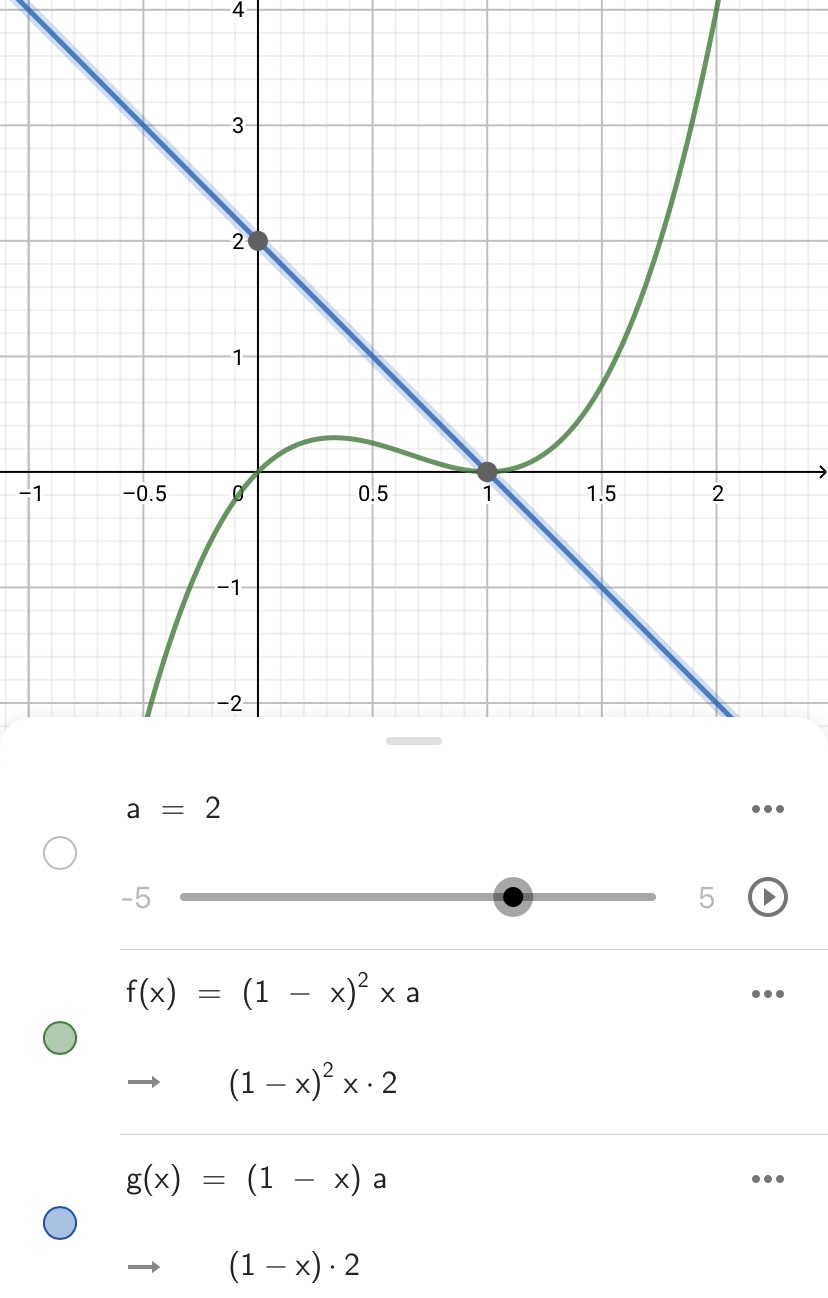
- 蓝色为交叉熵, 绿色为MSE
虽然看起来交叉熵的变化更平稳, 而且单调性很好, 但是因为自变量是模型输出, 我们并不知道实际上参数更新时到底平不平稳. 而且这个图给人一种错觉: 好像要是模型一开始的输出小于0.25, 那么就永远也学习不到正确的参数了.
下图是一个正确的例子, 图中也可以看出交叉熵作为损失的优越性.2
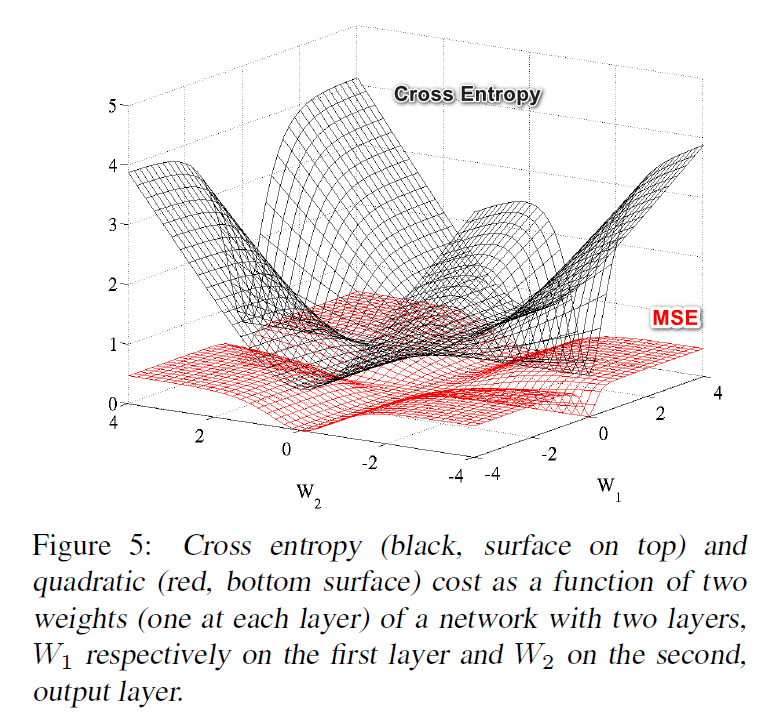
# Softmax
Softmax的情况太复杂了, 我们给出一些其他论文里面的论证:
一个验证实验的结果: Sigmoid-MSE vs. Softmax Cross-Entropy – Weights & Biases
- MSE也能够训练, 但是精确度要低一点
有一篇论文3探究了交叉熵与平方损失的不同, 对于梯度, MSE在Softmax里面有同样的问题: 距离最优值较远的时候梯度也很小:

# Others
- 网上看到这张图蛮有意思的, 但是他好像说的不太对4
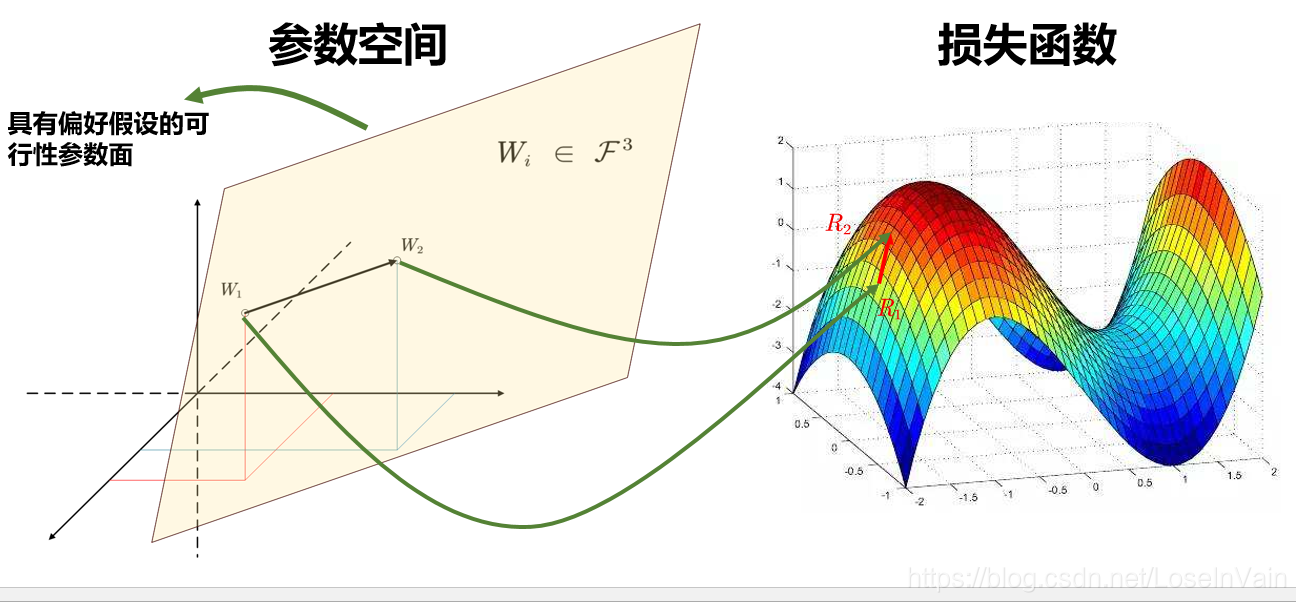
这篇文章是Xavier初始化的文章(zotero://select/items/@glorot2010understanding) ↩︎
P. Golik, P. Doetsch, and H. Ney, “Cross-entropy vs. squared error training: a theoretical and experimental comparison,”(zotero://select/items/@Golik2013CrossentropyVS) 2013. doi: 10.21437/Interspeech.2013-436 . ↩︎