对于等价的网络, 小的卷积核参数更少

Last updated Unknown Edit Source

• All

• 我们知道 2个3x3卷积核堆叠后等价于一个5x5卷积核, 以此为例我们来比较一下两者的参数大小.

卷积层参数大小的计算

• 假设输入通道数为 $C_{in}$, 输出通道数为 $C_{out}$

• 对于 $5\times5$ 卷积, 参数数量为: $$5\times5\times C_{in} \times C_{out}$$

• 对于 $3\times3$ 卷积, 假设第一次卷积的输出通道数为 $C_{mid}$

  • 一次 $3\times3$ 卷积的参数数量为 $$3\times3\times \textcolor{Orange}{C_{in}}\times \textcolor{ForestGreen}{C_{mid}}$$
  • 第二次卷积的参数数量为 $$3\times3\times \textcolor{ForestGreen}{C_{mid}}\times \textcolor{RoyalBlue}{C_{out}}$$
  • 总的参数数量为: $$9\times\textcolor{ForestGreen}{C_{mid}}\left(\textcolor{Orange}{C_{in}}+\textcolor{RoyalBlue}{C_{out}}\right)$$

• 如果输入输出频道数相同:

  • $5\times5$ 卷积: $$25\times C^2$$
  • $3\times3$ 卷积: $$18\times C^2$$
  • 显然更小的卷积核参数数量更少

• 如果输入输出频道数不同:

  • 对于 $3\times3$ 卷积:
    • 我们通常选取 $\textcolor{ForestGreen}{C_{mid}}$ 为 $\textcolor{Orange}{C_{in}},\textcolor{RoyalBlue}{C_{out}}$ 的几何平均数, 也就是说: $$\textcolor{ForestGreen}{C_{mid}}=\sqrt{\textcolor{Orange}{C_{in}}\textcolor{RoyalBlue}{C_{out}}}$$ 如果 $\textcolor{Orange}{C_{in}}\times \alpha=\textcolor{RoyalBlue}{C_{out}}$, 则 $$\textcolor{ForestGreen}{C_{mid}}=\sqrt{\alpha}\times\textcolor{Orange}{C_{in}}$$
  • 对比一下两者的参数数量:

    • $5\times5$ 卷积: $$25\times C_{in} \times C_{out}$$

    • $3\times3$ 卷积: $$9\times \sqrt{\textcolor{Orange}{C_{in}}\textcolor{RoyalBlue}{C_{out}}}\left(\textcolor{Orange}{C_{in}}+\textcolor{RoyalBlue}{C_{out}}\right)$$

    • 这个就不是很好比较了, 我们把图做出来看看: 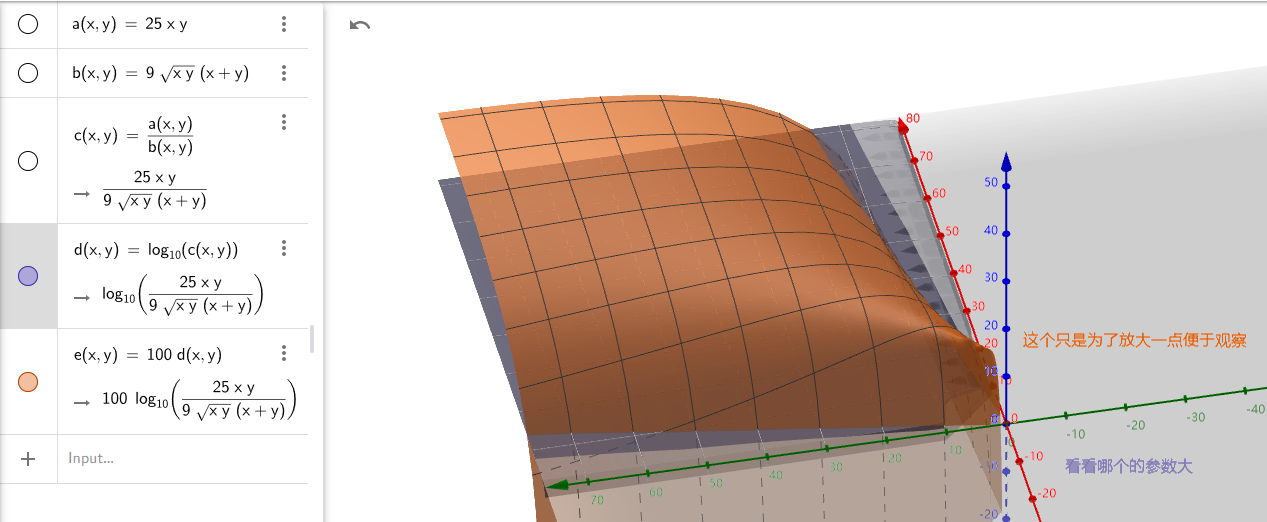¹

    • 可以看到一般的参数范围内, 都是小的卷积核参数更少.