D2L-24-数值稳定性

Last updated Feb 17, 2022 Edit Source

• All
• Deep learning
• Numerical computing
• Todo

Tags: #DeepLearning #NumericalComputing

• 数值稳定性的问题发生在反向传播的时候.
• 对于一个很深的模型, 计算在损失 $\ell$ 关于第 $t$ 层权重 $\mathbf{W_t}$ 的梯度的时候, 如果第 $t$ 层关于输出较远, 则结果由许多矩阵乘法构成, 这会导致梯度爆炸或者梯度消失.
  • 考虑如下有 $\mathrm{d}$ 层的神经网络 $$\mathbf{h}^{t}=f_{t}\left(\mathbf{h}^{t-1}\right) \quad \text { and } \quad y=\ell \circ f_{d} \circ \ldots \circ f_{1}(\mathbf{x})$$
  • 对于一个一百层的模型: $$1.5^{100} \approx 4 \times 10^{17} \quad 0.8^{100} \approx 2 \times 10^{-10}$$
  • 两者都远远超出了常用的16位浮点数能表示的最大值 $65504$ 和最小精度 $2^{-24}\approx 6e(-8)$

• 这是导致数值不稳定的根本问题
• 例子: MLP (为了简单省略了偏移) $$\mathbf{h}^{t}=f_{t}\left(\mathbf{h}^{t-1}\right)=\sigma\left(\mathbf{W}^{t} \mathbf{h}^{t-1}\right)$$
  • $\sigma$ 是激活函数 $$\frac{\partial \mathbf{h}^{t}}{\partial \mathbf{h}^{t-1}}=\operatorname{diag}\left(\sigma^{\prime}\left(\mathbf{W}^{t} \mathbf{h}^{t-1}\right)\right)\left(\mathbf{W}^{t}\right)^{T}$$¹
  • $\sigma^{\prime}$ 是 $\sigma$ 的导数函数, 则 $$\prod_{i=t}^{d-1} \frac{\partial \mathbf{h}^{i+1}}{\partial \mathbf{h}^{i}}=\prod_{i=t}^{d-1} \operatorname{diag}\left(\sigma^{\prime}\left(\mathbf{W}^{i} \mathbf{h}^{i-1}\right)\right)\left(\mathbf{W}^{i}\right)^{T}$$
• 我们选择ReLU作为激活函数, 则其导数为:

  • $$\sigma(x)=\max (0, x) \quad \text { and } \quad \sigma^{\prime}(x)= \begin{cases}1 & \text { if } x>0 \\ 0 & \text { otherwise }\end{cases}$$

  • 则前面的梯度为$$\prod_{i=t}^{d-1} \frac{\partial \mathbf{h}^{i+1}}{\partial \mathbf{h}^{i}}=\prod_{i=t}^{d-1} \operatorname{diag}\left(\sigma^{\prime}\left(\mathbf{W}^{i} \mathbf{h}^{i-1}\right)\right)\left(\mathbf{W}^{i}\right)^{T}$$

  • 其中 $\operatorname{diag}\left(\sigma^{\prime}\left(\mathbf{W}^{i} \mathbf{h}^{i-1}\right)\right)$ 是全部由0和1构成的对角矩阵. 这使得结果的一些元素来自于 $$\prod_{i=t}^{d-1} \left(W^{i} \right)^{T}$$

  • 在 $d-t$ 较大的时候, 如果其中出现大于1的数连乘, 则很可能出现梯度爆炸. 同样, 如果其中出现小于1的数连乘, 则很可能出现梯度消失.

• 除了矩阵连乘, 激活函数的导数值也可能导致数值问题
  • 例: $Sigmoid$ Function 它的导函数是: $$\sigma’(x)=\sigma(x)(1-\sigma(x))$$
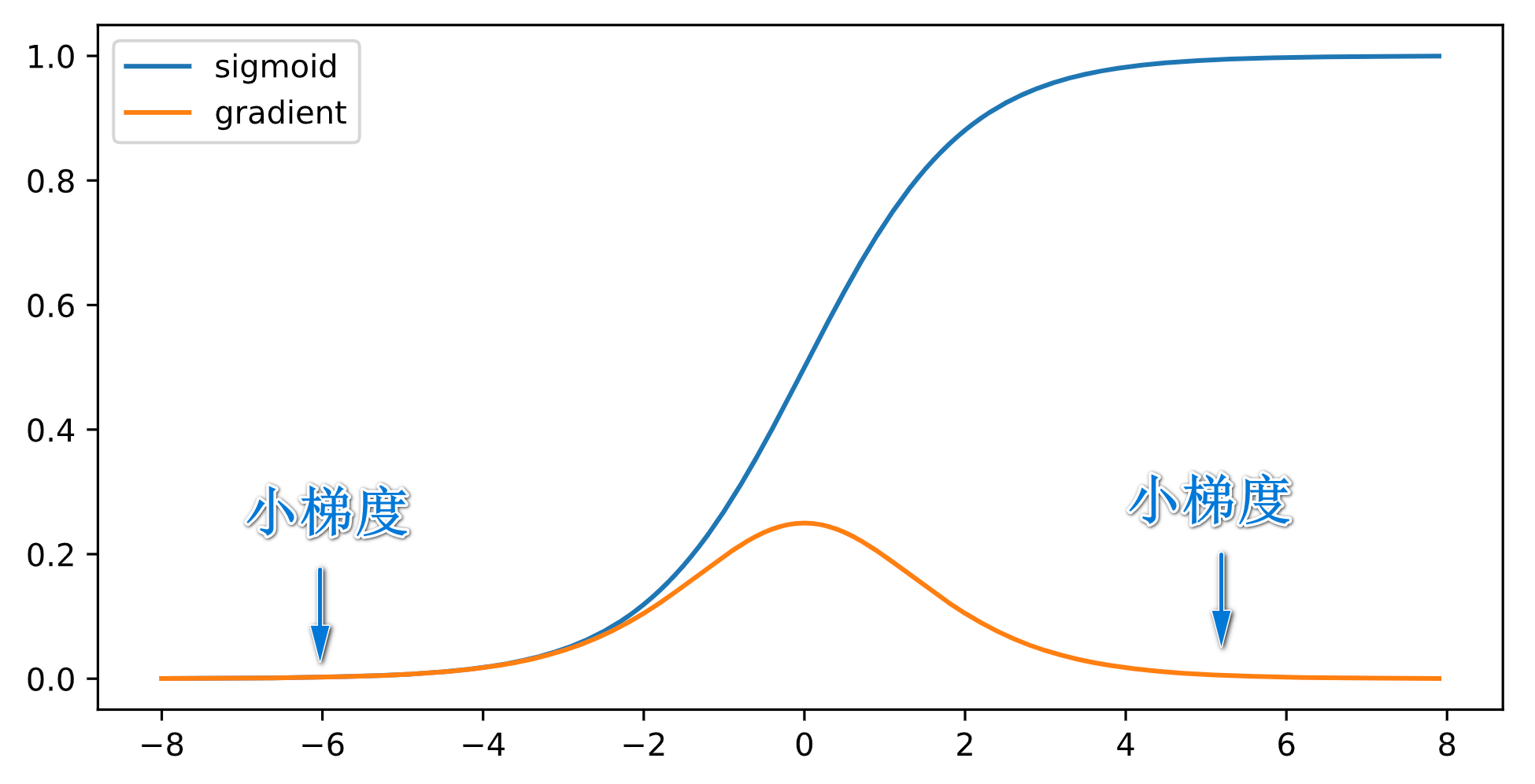
  • 当输入较大的时候, $\operatorname{diag}\left(\sigma^{\prime}\left(\mathbf{W}^{i} \mathbf{h}^{i-1}\right)\right)$ 会变得很小 ,则 $$\prod_{i=t}^{d-1} \frac{\partial \mathbf{h}^{i+1}}{\partial \mathbf{h}^{i}}=\prod_{i=t}^{d-1} \operatorname{diag}\left(\sigma^{\prime}\left(\mathbf{W}^{i} \mathbf{h}^{i-1}\right)\right)\left(\mathbf{W}^{i}\right)^{T}$$ 是 $d-t$ 个小数值的乘积. 这很容易造成梯度消失.

• 最直接的后果是梯度值超出范围

  • 梯度爆炸: inf, 梯度消失: 0

• 而这会导致训练的时候很难选择学习率

  • 梯度爆炸: 学习率被限制在一个很小的范围内. 太大了会导致梯度爆炸, 太小了则会导致训练缓慢.
    • 我们可能需要在训练时不断调整学习率
  • 梯度消失: 学习率无论怎么调整, 训练都没有进展

• 对于网络结构, 梯度消失会使得模型仅仅在靠近输出的一端训练的很好, 而靠近输入的一端则由于梯度消失, 完全得不到优化.