D2L-25-让训练更加稳定-Xavier初始化

Last updated Feb 18, 2022 Edit Source

• All
• Deep learning

Tags: #DeepLearning

• 因为我们无法改变 梯度问题的根本原因, 所以我们的目标是将梯度的值控制在一个合理的范围内.

• 将乘法变加法: 如ResNet, LSTM

• 归一化: 梯度归一化, Gradient Clipping-梯度剪裁

• 合理地初始化权重并选择合适的激活函数:

  • 初始化方案的选择在神经网络学习中起着举足轻重的作用， 它对保持数值稳定性至关重要。
  • 此外，这些初始化方案的选择可以与非线性激活函数的选择有趣的结合在一起。

目标: 我们可以将每层的输出 $h_i^s$ 和梯度 $\frac{\partial \ell}{\partial h_{i}^{s}}$ 都看做随机变量, 通过让它们的均值和方差都保持一致, 实现对梯度的归一化 $$\begin{gathered} \text{正向:}\quad\mathbb{E}\left[h_{i}^{s}\right]=0 \quad \operatorname{Var}\left[h_{i}^{s}\right]=a \\\ \text{反向:}\quad\mathbb{E}\left[\frac{\partial \ell}{\partial h_{i}^{s}}\right]=0 \quad \operatorname{Var} \left[\frac{\partial \ell}{\partial h_{i}^{s}}\right]=b \quad \forall i, s\end{gathered}$$ 其中 $a,b$ 均为常数.

• 我们可以通过合理的权重初始化来达到上面的目标
• 对于一个中等难度的问题, 框架默认的随机初始化通常很有效(例如 $\mathcal{N}(0,0.01)$ ), 但是对于很深的神经网络则难以保证效果.
• 现在标准且实用的一种方法叫做Xavier初始化

# Xavier初始化1

Xavier初始化的详细例子

• 从例子中可以看出, 如果正向反向都要保证方差一致, 那么需要同时满足 $n_{s}\gamma_{s}=1$ 和 $n_{s-1} \gamma_{s}=1$, 其中 $\gamma_s$ 是第 $s$ 层权重的方差, $n_{s-1}, n_{s}$ 是输入和输出的维度.

  • 因为隐藏层的输入和输出维度很可能不一致, 所以这其实是很难满足的.

• Xavier初始化则令 $$\frac{\gamma_{s}\left(n_{s-1}+n_{s}\right)}{2} =1 \quad \rightarrow\quad \gamma_{s}=\frac{2}{n_{s-1}+n_{s}}$$

  • 尽管在上述数学推理中，“不存在非线性”的假设在神经网络中很容易被违反， 但Xavier初始化方法在实践中被证明是有效的。

• 正态分布 $$\mathcal{N}\left(0, \sqrt{\frac{2}{n_{s-1}+n_{s}}}\right)$$

• 均匀分布 $$\mathscr{U}\left(-\sqrt{\frac{6}{n_{s-1}+n_{s}}}, \sqrt{\frac{6}{n_{s-1}+n_{s}}}\right)$$

  • 分布 $\mathscr{U}[-a, a]$ 的方差是 $a^{2} / 3$

• Bonus Question: 为什么参数不能初始化为同一个常数?

• 现在我们先假设损失函数是一个线性的函数 $\sigma(x)=\alpha x+\beta$, 来看看输入和输出的均值和方差经过 $\sigma(x)$ 后会有什么变化.

  • 令 $\mathbf{h}^{\prime}=\mathbf{W}^{t} \mathbf{h}^{t-1} \quad \text { and } \quad \mathbf{h}^{t}=\sigma\left(\mathbf{h}^{\prime}\right)$
  • 前面我们已经知道 $\mathbf{h}^{s}=\mathbf{W}^{s} \mathbf{h}^{s-1}$ 时, $\mathbb{E}(\mathbf{h}^{s})=\mathbb{E}(\mathbf{h}^{s-1})=0$. 且反向也一样, 所以我们根据方差的性质可以知道: $$\begin{aligned} \mathbb{E}\left[h_{i}^{t}\right] &=\mathbb{E}\left[\alpha h_{i}^{\prime}+\beta\right]=\beta \\ \operatorname{Var}\left[h_{i}^{t}\right] &=\mathbb{E}\left[\left(h_{i}^{t}\right)^{2}\right]-\mathbb{E}\left[h_{i}^{t}\right]^{2} \\ &=\mathbb{E}\left[\left(\alpha h_{i}^{\prime}+\beta\right)^{2}\right]-\beta^{2} \\ &=\mathbb{E}\left[\alpha^{2}\left(h_{i}^{\prime}\right)^{2}+2 \alpha \beta h_{i}^{\prime}+\beta^{2}\right]-\beta^{2} \\ &=\alpha^{2} \operatorname{Var}\left[h_{i}^{\prime}\right] \end{aligned}$$ 如果要保持均值和方差不变, 则要求 $\beta=0, \alpha=\pm1$
  • 反向也类似

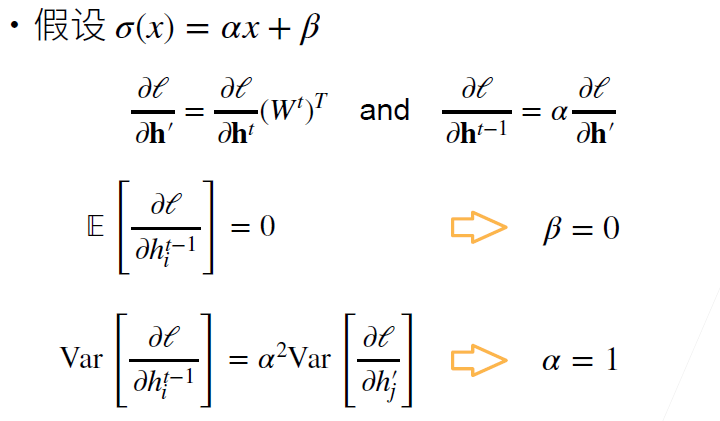
• 现在我们来检查各个激活函数的形状:

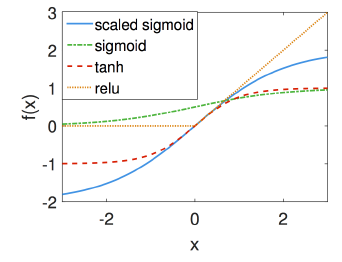
• 使用泰勒展开 $$\operatorname{sigmoid}(x)=\frac{1}{2}+\frac{x}{4}-\frac{x^{3}}{48}+O\left(x^{5}\right)$$ $$\tanh (x)=0+x-\frac{x^{3}}{3}+O\left(x^{5}\right)$$ $$\operatorname{ReLU}(x)=0+x \quad for\quad x \geq 0$$ 可以看到, 除了Sigmoid以外, 其他函数在原点附近都基本满足 $\alpha=\pm1, \beta=0$ 的条件.

• 我们可以规范化Sigmoid函数: $$\text{scaled Sigmoid: }=\quad 4\times \operatorname{Sigmoid}(x)-2$$ 减 $2$ 是为了让函数关于原点对称