D2L-26-环境和分布偏移

Last updated Feb 19, 2022 Edit Source

• All
• Deep learning
• Distribution shift
• Covariate shift

Tags: #DeepLearning #DistributionShift #CovariateShift

• 环境是变化的，数据也是。有时通过将基于模型的决策引入环境，我们可能会破坏模型¹。我们需要合理地调整模型来适应这种可能的变化。

• 顾名思义，就是输入数据（特征、协变量）的分布发生了偏移。也就是说，输入变得不一样了，原来是真实的猫猫狗狗， 现在变成了卡通的猫猫狗狗！
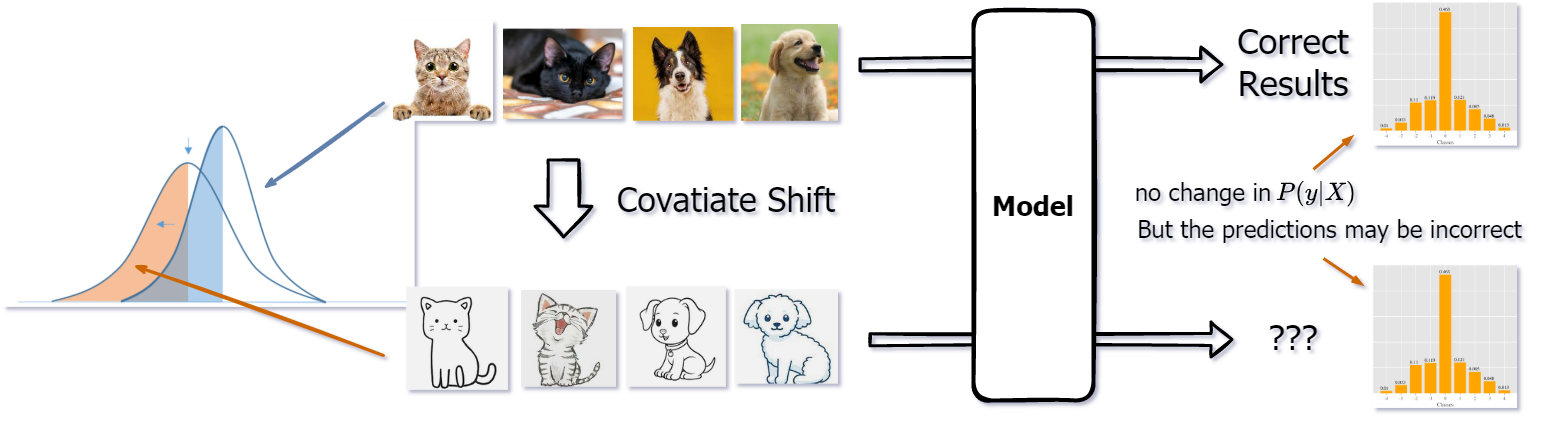
• 形式化地说, 就是输入数据的分布 $P(X)$ 发生了变化, 但是在输入确定之后, 最终输出的标签分布 $P(y\space |\space X)$ 不变.

• 协变量偏移是输入的原始数据分布发生了偏移, 而标签偏移则是原始数据对应的标签分布发生了偏移.
• 比如在鼠疫的诊断上, 鼠疫最初的症状有头痛、双眼充血、咳嗽、以及怠倦感，与普通呼吸道疾病相似。虽然其症状在十三世纪时和现在都是差不多的, 但是随着医学的进步, 鼠疫的发病率已经大大降低了. 所以现在面对相同的症状, 诊断为呼吸道疾病的概率是要大于鼠疫的. 也就是说, 在鼠疫的判断问题上发生了标签偏移. ²
• 形式化地来说, 就是一个标签对应的特征分布 $P(X\space |\space y)$ 不变, 而标签的边缘概率分布 $P(y)$ 发生了变化.

• 直观的理解, 概念分布就是一个事物的定义(概念)发生了变化, 比如下图表示了美国不同地区对于Soft Drink的不同定义:

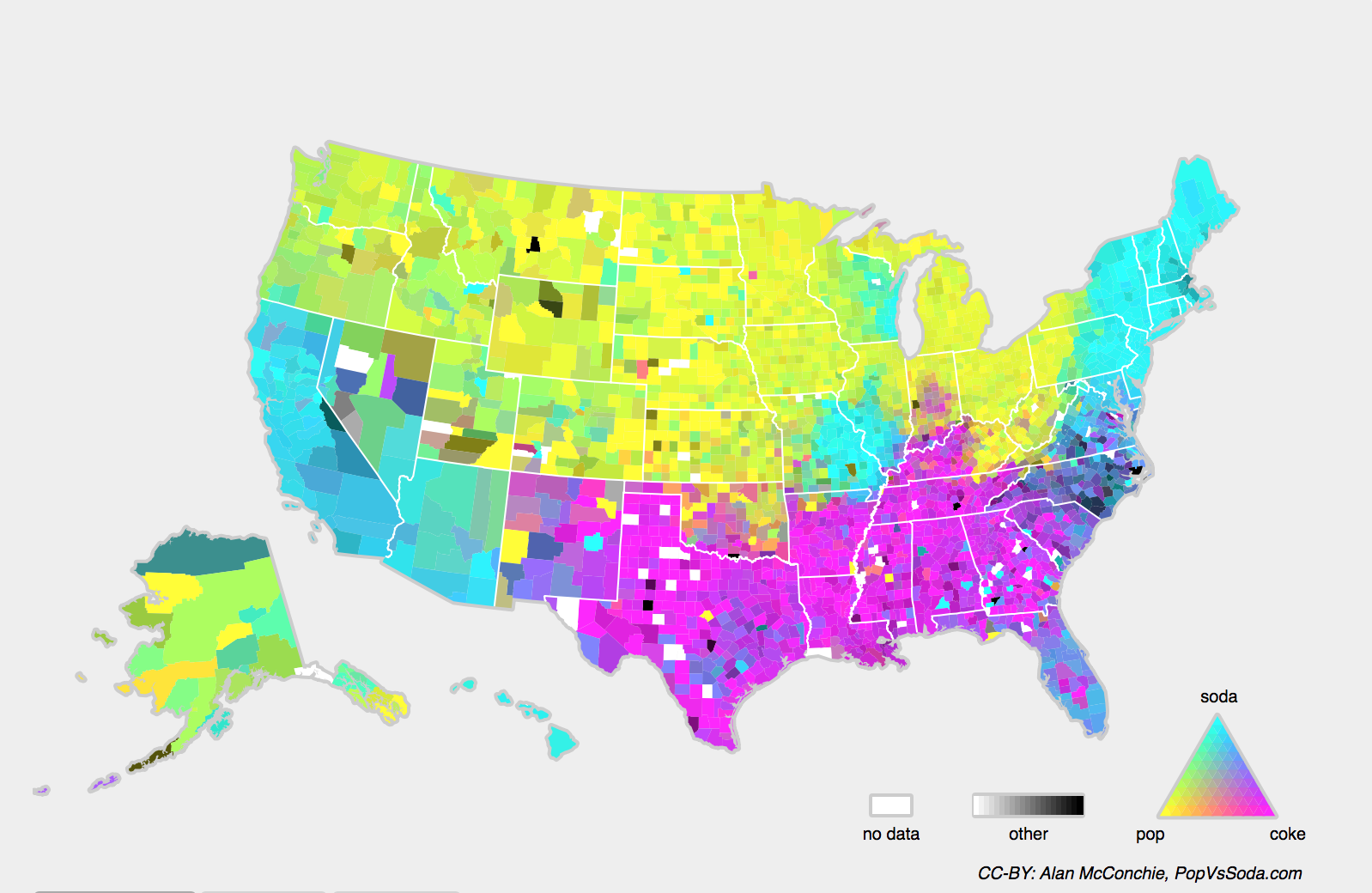
• 形式化地来说, Concept Shift就是 $X$ 与 $y$ 的相互关系发生了变化³, 而它们的概率分布可能不变.

• 更多的例子: Environment and Distribution Shift — Examples of Distribution Shift

对于训练数据 $\left{\left(\mathbf{x}{1}, y{1}\right), \ldots,\left(\mathbf{x}{n}, y{n}\right)\right}$, 我们最小化损失函数的过程可以表示为: $$\operatorname{minimize} \frac{1}{n} \sum_{i=1}^{n} l\left(f\left(\mathbf{x}{i}\right), y{i}\right)$$ 在统计的语境里面, 上面的损失也称为 经验损失 (Empirical Risk). 也就是损失 $l(f(\mathbf{x}), y)$ 在整个数据的真实分布 $p(\mathbf{x}, y)$ 上面的数学期望: $$E_{p(\mathbf{x}, y)}[l(f(\mathbf{x}), y)]=\iint l(f(\mathbf{x}), y) p(\mathbf{x}, y) d \mathbf{x} d y$$ 但是在实际过程中我们不知道数据的真实分布 $p(\mathbf{x}, y)$, 所以我们只能近似地去最小化Empirical risk.

• 假设由于Covariate Shift, 特征的分布由 $q(\mathbf{x})$ 偏移到了 $p(\mathbf{x})$, 并且标签的分布没有发生变化: $q(y \mid \mathbf{x})=p(y \mid \mathbf{x})$. 则我们可以用如下等式来对原来的模型进行修正: $$\iint l(f(\mathbf{x}), y) p(y \mid \mathbf{x}) p(\mathbf{x}) d \mathbf{x} d y=\iint l(f(\mathbf{x}), y) q(y \mid \mathbf{x}) q(\mathbf{x}) \textcolor{red}{\frac{p(\mathbf{x})}{q(\mathbf{x})}} d \mathbf{x} d y$$
• 可以看到关键便是利用系数 $\beta_{i}$ 来对每一个样本 $\mathbf{x}{i}$ 进行修正: $$\beta{i} \stackrel{\text { def }}{=}\frac{p\left(\mathbf{x}{i}\right)}{q\left(\mathbf{x}{i}\right)}$$
• 最小化损失函数的过程变为了 $$\underset{f}{\operatorname{minimize}} \frac{1}{n} \sum_{i=1}^{n} \textcolor{red}{\beta_{i}} l\left(f\left(\mathbf{x}{i}\right), y{i}\right)$$

• 因为训练样本是已知的, 所以 $q(\mathbf{x})$ 很好计算, 但是偏移之后的 $p(\mathbf{x})$ 则不是很好计算. 尽管有一些花哨的方法⁴可以用来估计 $\beta_{i}$ , 但我们也可以用简单的 Logistic_Regression来解决这个问题:

• 我们的想法是: 利用Logistic Regression来训练一个分类器, 用来区分 $p(\mathbf{x})$ 和 $q(\mathbf{x})$.

  • 如果分类器不能区分的话, 说明这个样本没有发生偏移;
  • 对应的, 要是分类器能够区分的话, 我们便利用分类器的输出对样本进行相应的加权(利用Logistic回归的输出来生成权重 $\beta_{i}$)

• 为了简单起见, 我们假设 $p(\mathbf{x})$ 和 $q(\mathbf{x})$ 有同样数量的样本 $X=\mathbf{{x_1,\cdots, x_n}}$ 和 $U=\mathbf{{u_1,\cdots, u_n}}$, 对于从新的分布 $p$ 里面采样的样本, 我们令标签 $z=1$, 从旧的分布 $q$ 里面采样的样本, 我们令标签 $z=-1$, 则得到样本集合: $$\left{\left(\mathbf{x}{1},-1\right), \ldots,\left(\mathbf{x}{n},-1\right),\left(\mathbf{u}{1}, 1\right), \ldots,\left(\mathbf{u}{m}, 1\right)\right}$$

  • 因为有: $$P(z=1 \mid \mathbf{x})=\frac{p(\mathbf{x})}{p(\mathbf{x})+q(\mathbf{x})} \text{ and }P(z=-1 \mid \mathbf{x})=\frac{q(\mathbf{x})}{p(\mathbf{x})+q(\mathbf{x})}$$
  • 两式相除: $$ \frac{P(z=1 \mid \mathbf{x})}{P(z=-1 \mid \mathbf{x})}=\frac{p(\mathbf{x})}{q(\mathbf{x})}$$
  • 我们又知道 $$P(z=1 \mid \mathbf{x})=\frac{1}{1+\exp (-h(\mathbf{x}))}$$
  • 所以有: $$\beta_{i}=\frac{1 /\left(1+\exp \left(-h\left(\mathbf{x}{i}\right)\right)\right)}{\exp \left(-h\left(\mathbf{x}{i}\right)\right) /\left(1+\exp \left(-h\left(\mathbf{x}{i}\right)\right)\right)}=\exp \left(h\left(\mathbf{x}{i}\right)\right)$$
  • 这便是权重的估计值, 如果考虑到范围还可以约束为 $\beta_{i}=\min \left(\exp \left(h\left(\mathbf{x}_{i}\right)\right), c\right)$, $c$ 为常量.
  • 注意上面的算法依赖于一个重要的假设： 需要目标分布中的每个数据样本在训练时出现的概率非零(就是说偏移后的数据也得在原来的分布里面存在: $q(\mathbf{x})\neq0$ )。 如果我们找到 $p(\mathbf{x})>0$ 但 $q(\mathbf{x})=0$ 的点， 那么相应的权重 $\beta_{i}$ 会是无穷大。

• 标签偏移的纠正方法和上面很相似. 我们假设标签的分布从 $q(y)$ 偏移到了 $p(y)$, 同时每一个类的特征分布是不变的: $q(\mathbf{x} \mid y)=p(\mathbf{x} \mid y)$. 那么我们可以根据下面的等式来纠正标签偏移: $$\iint l(f(\mathbf{x}), y) p(\mathbf{x} \mid y) p(y) d \mathbf{x} d y=\iint l(f(\mathbf{x}), y) q(\mathbf{x} \mid y) q(y) \textcolor{red}{\frac{p(y)}{q(y)}} d \mathbf{x} d y$$
• 同样, 修正的权重可以定义为: $$\beta_{i} \stackrel{\text { def }}{=} \frac{p\left(y_{i}\right)}{q\left(y_{i}\right)}$$
• 训练数据里面的标签分布 $q(y_{i})$ 是已知的, 所以我们只需要估计 $p(y_{i})$

• 如果标签偏移的程度不是特别大, 我们其实可以将原始的标签 $q(\mathbf{y})$ 进行线性变换来得到新的输出: $p(\mathbf{y})$

• 详细的来说, 我们可以构造一个 $k\times k$ 的混淆矩阵⁵ $C$ ($k$ 是类别的数目). 其中列索引对应Validation set数据的真实标签, 行索引则对应模型的输出标签. 每一个元素 $c_{ij}$ 的值则是整个Validation Set里面, 模型把类别 $j$ 预测为类别 $i$ 的概率.

  • 举个例子, 要是数据没有发生偏移, 那么C就是一个单位矩阵. 模型和单位矩阵差的越多, 标签偏移就越严重.

• 我们可以将模型实际预测时的结果记录下来, 得到输出 $\mu(\hat{\mathbf{y}}) \in \mathbb{R}^{k}$, 其中第 $i$ 个分量 $\mu\left(\hat{y}_{i}\right)$ 是模型预测值为 $i$ 的概率.

• 将所有模型输出为 $i$ 的情况统计起来, 有 $$\sum_{j=1}^{k} c_{i j} p\left(y_{j}\right)=\mu\left(\hat{y}_{i}\right)$$

• 所以 $$\mathbf{C} p(\mathbf{y})=\mu(\hat{\mathbf{y}})$$

• 只要这个分类器在一开始是足够准确的, 并且偏移的程度不太大, 那么矩阵C就是可逆的, 我们便能够根据 $C$ 和 $\mu(\hat{\mathbf{y}})$ 近似得到新的标签分布 $p(\mathbf{y})=C^{-1}\mu(\hat{\mathbf{y}})$

• 概念偏移通常是很难修正的, 因为"X和y相互关系的变化"通常很难衡量. 举个极端的例子, 将分类猫猫狗狗的分类器拿去区分老虎和大象, 效果肯定不好. 这时候通常我们只能重新收集数据进行训练.