D2L-32-Convolution-卷积
# 卷积 - Convolution
Tags: #DeepLearning #Convolution
关键点:
Convolution Determines the Output of a System for any Input1
从数学的角度理解, 卷积是通过两个函数 ($f$ 和 $g$ ) 生成第三个函数 ($fg$) 的一种数学算子, 卷积函数 $fg$ 表示了两个函数相互影响的结果.
# 卷积: 直观理解
# 卷积可以衡量许多瞬时输入的累计影响
The Motivation of Convolution 这是一个交互的例子, 强烈建议点进去
- 以室外温度对室内温度的影响为例, 假设某一天的气温对于以后几天的室内温度的影响呈如下指数分布:
- 我们可以看到影响随着时间的增长衰减的很快.
- 显然室外温度变化是一个连续的函数, 如下面蓝色曲线所示. 而这个蓝色曲线上每一点对室内气温的影响的变化, 都是上方的红色曲线.
- 我们怎样衡量今天以前所有的室外气温对今日气温的总影响呢? 这就要求我们计算无数个瞬时输入的累计影响, 而卷积可以做到这一点:
- 我们计算 $f(\lambda)\cdot h(t-\lambda)$ 相对于 $\lambda$ 的变化曲线:
- 这就是 $t$ 时刻, 所有影响在时间上的分布, 为了计算累计影响, 我们需要对这个函数关于 $\lambda$ 进行积分: $$y(t)=\int_{-\infty}^{+\infty} h(t-\lambda) \cdot f(\lambda) \cdot d \lambda$$
- 上式就是卷积 $y(t)=h*f$ 的定义, 通过衡量输入 $f$ 在 $t$ 时刻以前的所有影响 $h$, 我们得到了累计影响随着时间的变化 $y(t)$
- 我们计算 $f(\lambda)\cdot h(t-\lambda)$ 相对于 $\lambda$ 的变化曲线:
- 以室外温度对室内温度的影响为例, 假设某一天的气温对于以后几天的室内温度的影响呈如下指数分布:
Some minor points
- 因为衡量的是 $t$ 时刻以前的累计影响, 所以我们需要"翻转"影响函数 $h$ 再进行"滑动".
- 对于每一个时刻 $t$, 我们都需要计算整个坐标轴上面所有点对于 $t$ 时刻的影响, 这也是为什么 $y(t)$ 的定义里面有一个积分符号.
- Live Demo
# 其他理解
- 下面是两个从离散变量角度来理解的例子
- 这是卷积在图像处理时的应用.
# 卷积的数学定义
$$(f * g)(t):=\int_{-\infty}^{\infty} f (\tau) g (t-\tau) d \tau$$
# 一些性质2
交换律Commutativity: 既然可以 $g$ 滑动 $f$ 不动, 那么肯定也可以 $f$ 滑动 $g$ 不动, 它们重叠的面积肯定是不会变的, 这就有了交换律: $$(f * g)(t)=\int_{-\infty}^{\infty} f (\tau) g (t-\tau) d \tau=\int_{-\infty}^{\infty} f (t-\tau) g (\tau) d \tau$$ in short: $$f * g=g * f$$
结合律Associativity: 假设有函数 $f,g,h$, 那么可以先叠加 $f$ 和 $g$ 的影响, 再叠加 $h$ 的影响, 也可以相叠加 $g$ 和 $h$ 的影响, 再叠加 $f$ 的影响, 结果肯定是不变的. $$f *(g * h)=(f * g) * h$$
分配律Distributivity: $$f *(g+h)=(f * g)+(f * h)$$
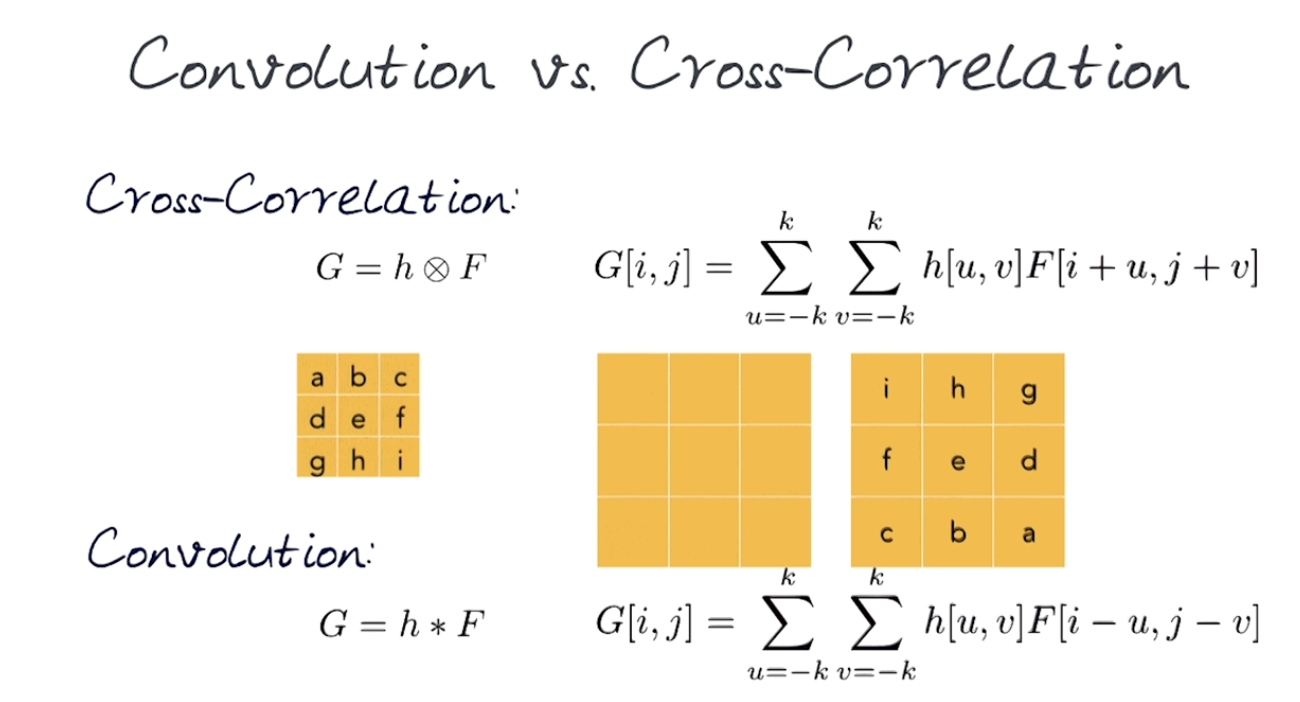
# 卷积与交叉相关 Convolution & Cross-Correlation
来源: 3
# 啥是交叉相关
Cross-correlation - Wikipedia 实数域上, 交叉相关是 $$(f \star g)(t) := \int_{-\infty}^{\infty} f(\tau) g(t+\tau) d \tau$$ 交叉相关和卷积就差了一个正负号
- In signal processing, cross-correlation is a measure of similarity of two series (序列) as a function of the displacement of one relative to the other.
交叉相关用于衡量图片相似度的一个例子
两者的差别不大, 含义都是类似的.
在计算卷积核的时候, 实际上我们计算的是交叉相关, 这是深度学习里面的一个术语误用.
# 数值计算: 卷积与傅里叶变换
卷积的计算复杂度是很高的, 所以我们想要找到一个高效的方法来计算卷积, 幸运的是, 卷积与傅里叶变换有以下联系 (Convolution Theorem): $$\mathcal{F}(fg)=\mathcal{F}(f)\mathcal{F}(g)$$ 也就是说 $$fg=\mathcal{F}^{-1}\left(\mathcal{F}(f)\mathcal{F}(g)\right)$$ 我们可以用傅里叶变换来代替卷积运算.
推导:
对于Cross-Correlation也是一样的, 只不过是在推导的时候把 $t-\tau$ 变成 $t+\tau$
Fast Fourier transfer (FFT) reduces the complexity of convolution from $𝑂(𝑛^2)$ to $𝑂(𝑛\log𝑛)$
GPU-accelerated FFT implementations perform up to 10 times faster than CPU only alternatives. (e.g. NVIDIA CUDA libraries) .
一个更详细的实例解释
下一部分谈论卷积神经网络