D2L-33-卷积神经网络CNN

Last updated Feb 26, 2022 Edit Source

• All
• Cnn
• Deep learning
• Convolution

Tags: #CNN #DeepLearning #Convolution

随着图像分辨率的提高, MLP显露出以下不足:

• 假设我们的图像分辨率为 $1920\times 1080$, 那么一张图片就有 $2,073,600$ 个像素点, 假设和输入层相连的隐藏层有 $1000$ 个单元, 那么光是第一个全连接层就有大约 $2\times10^9$ ($20$ 亿) 个参数, 训练这样的网络是难以想象的, 况且这还只是网络的第一层.

• 为了减少网络参数的大小, 我们需要想办法缩减参数的大小.

之前 MLP 的输入输出都是一维的： 图像可以看作像素点构成的二维矩阵。如果网络输入输出的形状都是二维的矩阵的话, 那么网络每一层的权重会变成一个四维张量: 规范地说, 就是: $$h_{i, j}=\sum_{k, l} w_{i, j, k, l} x_{k, l}$$ 其中索引 $k,l$ 的作用是对于每一个隐藏单元, 遍历所有输入 $X$; 索引 $i,j$ 的作用是遍历所有的隐藏单元（$H_h\times H_w$）.

¹

• 在一张图片里面平移一个物体, 这个物体的形状应该是不变的. 所以我们想, 能不能利用这种相似性来减少参数的大小呢?

• Parameter Sharing : 既然物体在图像哪里的形状都一样, 那么在图像任意位置识别这个物体的权重也大致相似. 也就是说, 我们可以在各个隐藏单元之间"分享权重".

• 数学上说, 就是: $$h_{i, j}=\sum_{k, l} w_{k, l} x_{k, l}$$ 权重不再和隐藏单元的索引 $i,j$ 相关了, 所有隐藏单元的权重都是同一个矩阵. 这是一个很大的进步!

• 平移不变性还意味着输入中"物体的平移"将导致输出中"激活的平移"

• 一张图像可以看作一团像素点, 而图像中相隔较远的像素点往往联系不大. 我们可以利用这种"重要性的衰减"来进一步缩减参数的大小.
• 要缩减我们关注像素点的范围, 自然需要减小权重矩阵的大小, 为了方便数学上的表示, 我们对索引 $k,l$ 进行以下变换: $$\begin{aligned}h_{i, j}&=\sum_{k, l} w_{k, l} x_{k, l}\\ &=\sum_{a, b} v_{a, b} x_{i+a, j+b} \end{aligned}$$
  • 其中 $w_{k,l}=v_{i+a, j+b}$ , 如果 $x$ 下标的范围不变, 这就意味着 $a\in[-i,k-i],$ $b\in[-j,l-j]$, 其实就相当于"以 $(i, j)$ 为中心开始计算 $h_{i, j}$ "
• 缩减参数的范围意味着要丢弃距离 $(i, j)$ 太远的权重, 也就是说： 当 $|a|,|b|>\Delta$ 时, 使得 $v_{a, b}=0$ $$h_{i, j}=\sum_{a=-\Delta}^{\Delta} \sum_{b=-\Delta}^{\Delta} v_{a, b} x_{i+a, j+b}$$

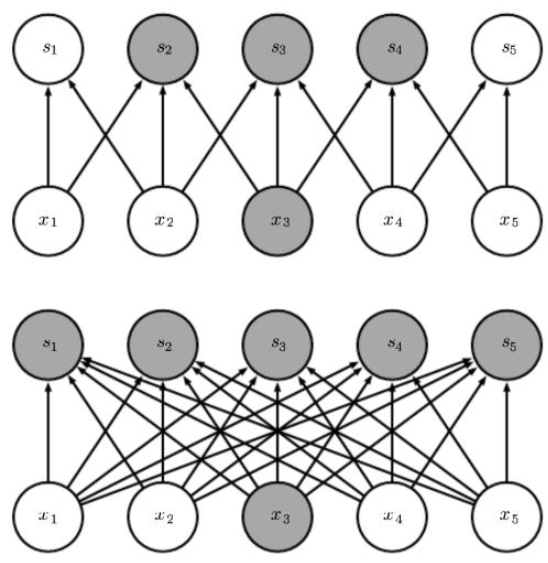
• 平移不变性和局部性是我们对全连接层的进一步约束, 也就是说: 卷积是一种特殊的全连接层.

• 相比全连接层 (FC Layer), 卷积层有更少的参数, 自然有着更快的运算速度与更小的存储开销

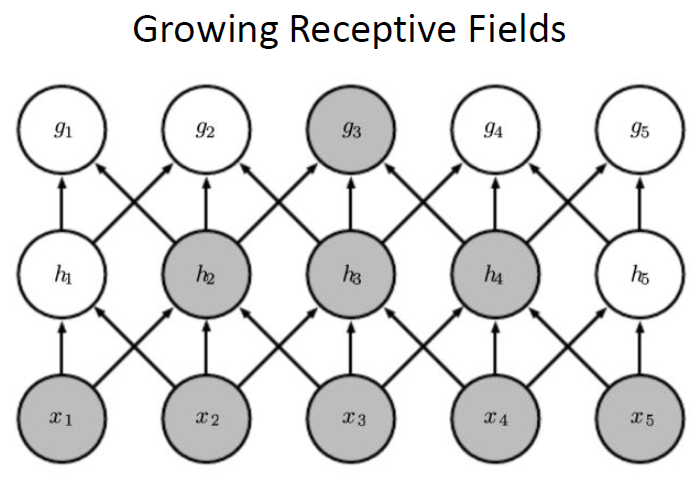
• 局部性是否意味着深度神经网络只注意细节而"不观大局"呢?
• 其实深度神经网络里面较深的层通常能间接地 (Indirectly) 关联更多的输入, 这使得神经网络能够从简单而稀疏的关系中组合出复杂的结构.
• 例如, 上图中第二层的 $h_i$ 只关联了3个输入, 而 $g_3$ 关联了所有五个输入.

卷积层的 归纳偏置 Inductive bias

• 卷积层中所有的权重学习都将依赖于归纳偏置(即局部性和平移不变性)。当这种偏置与现实相符时，我们就能得到样本有效的模型，并且这些模型能很好地泛化到未知数据中。
• 但如果这偏置与现实不符时，比如当图像不满足平移不变时，我们的模型可能难以拟合我们的训练数据。

一个例子: We build a face detector. It works well on all benchmarks. Unfortunately it fails on test data—the offending examples are close-ups where the face fills the entire image (no such data were in the training set).²

• 上面我们只是单纯地将图像看作像素点的二维矩阵, 但是实际上彩色图像有RGB三个通道 (Channel). 也就是说: 图像不是二维张量，而是一个由高度、宽度和颜色组成的三维张量.

• 因此，我们将 $X$ 索引为 $x_{i, j, k}$ . 对于图像的不同通道, 我们单独设置一个权重矩阵 $v_{a,\space b,\space i}$, 由此卷积相应地调整为 $v_{a,\space b,\space c}$ , 最后我们将不同输入通道的卷积结果相加: $$h_{i, j}=\sum_{a=-\Delta}^{\Delta} \sum_{b=-\Delta}^{\Delta}\sum_c v_{a,\space b,\space c}\space x_{i+a,\space j+b,\space c}$$

  • 现在我们将一个三维的图像 $X_{ijk}$ 变换为了一个二维的图像 $H_{ij}$, 权重变成了一个三维的张量 $v_{a,\space b,\space c}$

• 类比图像的颜色通道, 我们的隐藏表示 $H$ 能否也采用三维张量呢?

  • 实践表明这样是可以增强网络的表现能力的³, 这些通道有时也被称为_特征映射_（feature maps），因为每个通道都向后续层提供一组空间化的学习特征。
  • 直观上你可以想象在靠近输入的底层，一些通道专门识别边缘，而一些通道专门识别纹理。换句话说，对于每一个空间位置，我们采用一组而不是一个隐藏表示。 ⁴

• 为了支持输入 $X$ 和隐藏表示 $H$ 中的多个通道，我们可以在权重 $V$ 中添加第四个坐标，即 $v_{a,\space b,\space c,\space d}$ , 综上所述: $$h_{i,\space j,\space d}=\sum_{a=-\Delta}^{\Delta} \sum_{b=-\Delta}^{\Delta}\sum_c v_{a,\space b,\space c,\space d}\space x_{i+a,\space j+b,\space c}$$

  • 多个隐藏层通道意味着每一层有许多"块"不同的卷积核.

• CNN就是Kernel学习机器:
  • CNN学习到Kernel, 用这些Kernel处理输入, 得到隐藏层里面不同的特征: ✂️ From Kernel to CNN - YouTube