D2L-34-卷积层 - 填充 - Padding
# Padding - 填充
Tags: #DeepLearning #CNN #Padding
It’s always nice to have an interactive example:
卷积操作会使图像尺寸变小, 填充 (Padding) 可以减缓这个过程.
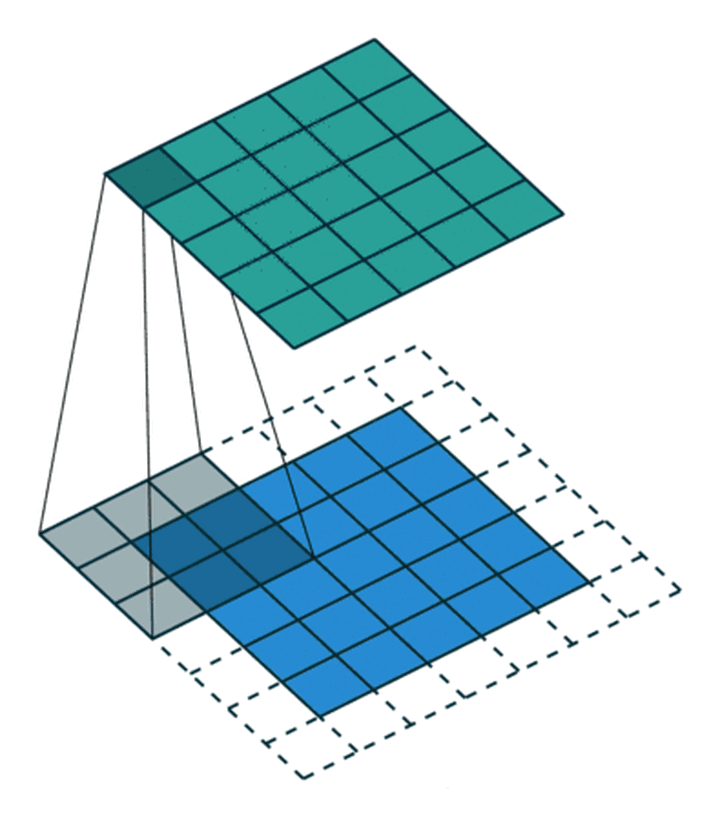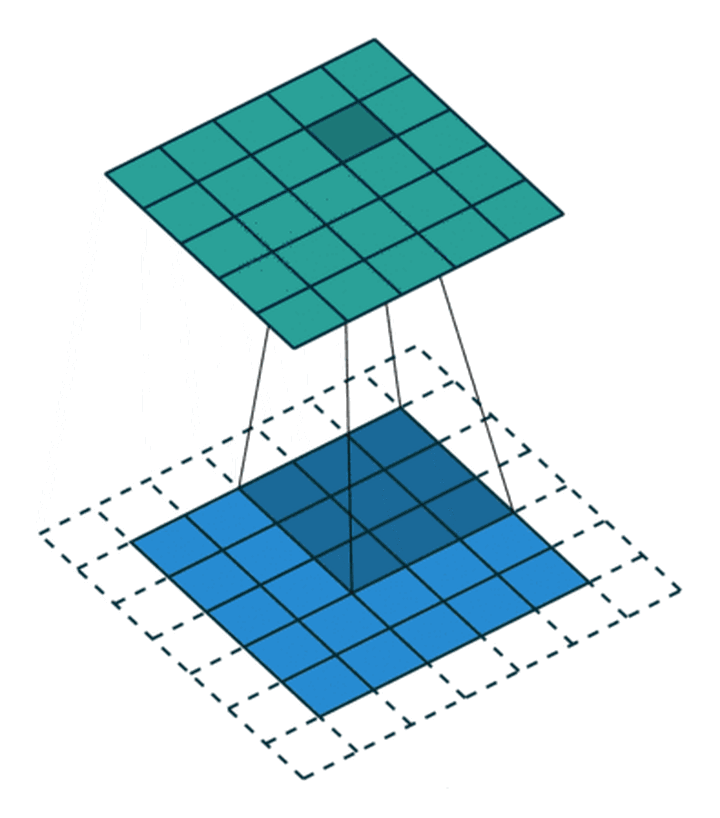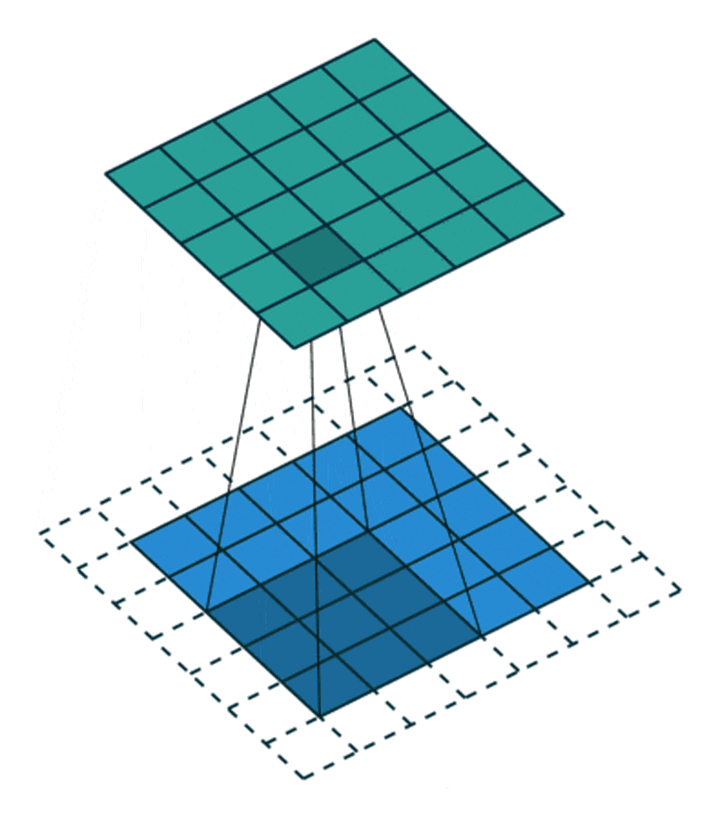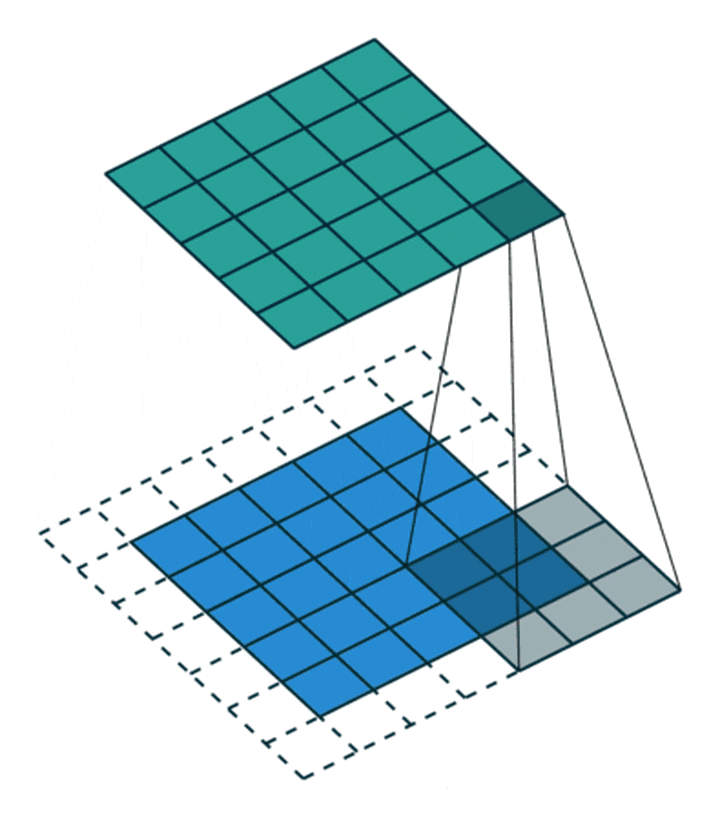
# 尺寸变化: 定量计算
我们假设输入的大小为 $x_h\times x_w$, 卷积核的大小为 $k_h\times k_w$
不带Padding的卷积: $$x_h\times x_w \quad\stackrel{conv}{\longrightarrow}\quad \left (x_{h}-k_{h}+1\right) \times\left (x_{w}-k_{w}+1\right)$$
假设Padding大小为 $p_h\times p_w$, 其中 $p_h$ 代表对height的填充(大约一半在顶部,一半在底部), $p_w$ 代表对width的填充(大约一半在左侧,一半在右侧)
注意这里的填充和Pytorch里面的padding有一点不同: Pytorch里面的
Padding=(4, 2)是指height中, 上面填充4排, 下面也填充四排, width同理.填充后图像大小增加相应的值: $$x_h\times x_w \quad\stackrel{conv}{\longrightarrow}\quad \left (x_{h}-k_{h}+1+p_{h}\right) \times\left (x_{w}-k_{w}+1+p_{w}\right)$$
# 填充大小的选取
在许多情况下,我们需要设置 $p_h=k_h−1$ 和 $p_w=k_w−1$,使输入和输出具有相同的高度和宽度 ($x_{h}-k_{h}+1+k_h−1=x_h$)。
假设 $k_h$ 是奇数,我们将在高度的两侧填充 $p_h/2$ 行。 但是如果 $k_h$ 是偶数,则一种可能性是在输入顶部填充 $⌈p_h/2⌉$ 行,在底部填充 $⌊p_h/2⌋$ 行,宽度同理。
- 所以卷积神经网络中卷积核的高度和宽度通常为奇数,例如1、3、5或7。这样保持空间维度的同时,我们可以在顶部和底部填充相同数量的行,在左侧和右侧填充相同数量的列。
最全面的大小计算公式
