KL_Divergence-KL散度

Last updated Feb 11, 2022 Edit Source

• All
• Math probability
• Deep learning

Tags: #Math/Probability #DeepLearning

¹

• KL散度可以衡量两个概率分布之间的相似性

• KL散度也称为相对熵

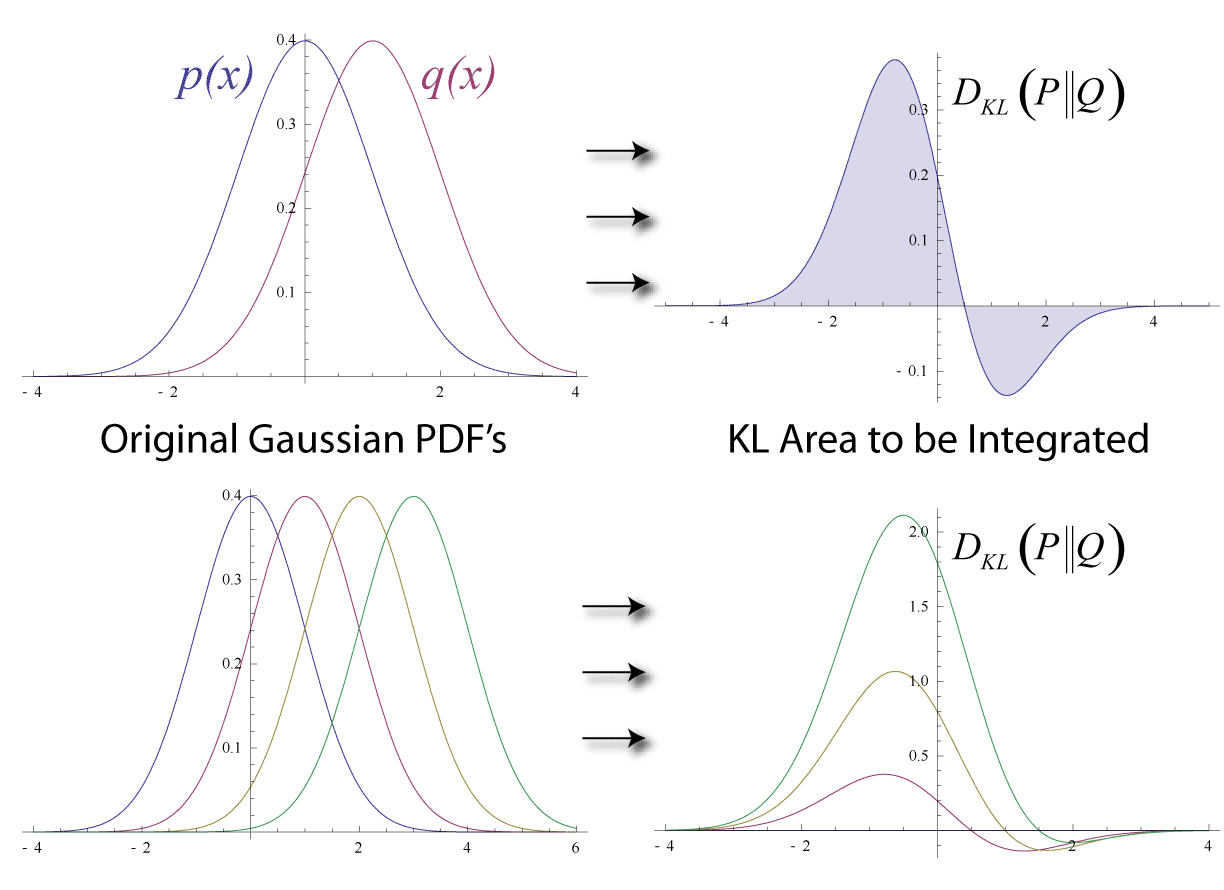
• Wikipedia: In mathematical statistics, the Kullback–Leibler divergence, $D _{KL} ( P ∥ Q )$ (also called relative entropy), is a statistical distance: a measure of how one probability distribution Q is different from a second, reference probability distribution P.

• 要理解相对熵是怎样衡量概率分布之间的差异的, 请看下面这个视频:

²

• 在机器学习里面, $D _{KL} ( P ∥ Q )$ 也被称为从Q切换到P的信息增益.
• 交叉熵越小, 说明两个概念越相似, 也就是PQ之间切换的信息增益越小.

• 对于相同概率空间 $\mathcal{X}$ 里面的离散概率分布 $P$ 和 $Q$, $P$相对于$Q$的相对熵定义如下: $$ D_{\mathrm{KL}}(P | Q)=\sum_{x \in \mathcal{X}} P(x) \log \left(\frac{P(x)}{Q(x)}\right) . $$ 也可以提一个负号出来: $$ D_{\mathrm{KL}}(P | Q)=-\sum_{x \in \mathcal{X}} P(x) \log \left(\frac{Q(x)}{P(x)}\right) $$

# 性质3

• 相对熵的值为非负数： $$D_{\mathrm{KL}}(P | Q) \geq 0,$$

  • 由吉布斯不等式可知，当且仅当 $P=Q$ 时 $D_{K L}(P | Q)$ 为零。这时两个分布具有相同的信息量.

• KL散度不具有对称性: 从分布 $P$ 到 $Q$ 的距离通常并不等于从 $Q$ 到 $P$ 的距离。 $$D_{\mathrm{KL}}(P | Q) \neq D_{\mathrm{KL}}(Q | P)$$

  • 原因很简单, 一个是$P(x)$在$log$外面, 另外一个是$Q(x)$在$log$外面
  • 尽管从直觉上 KL 散度是个度量或距离函数, 但是它实际上并不是一个真正的度量或距离。