Norm in Regularization - Intuition
# Norm in Regularization - Intuition
2022-02-14
Tags: #Norm #Regularization #DeepLearning #MachineLearning
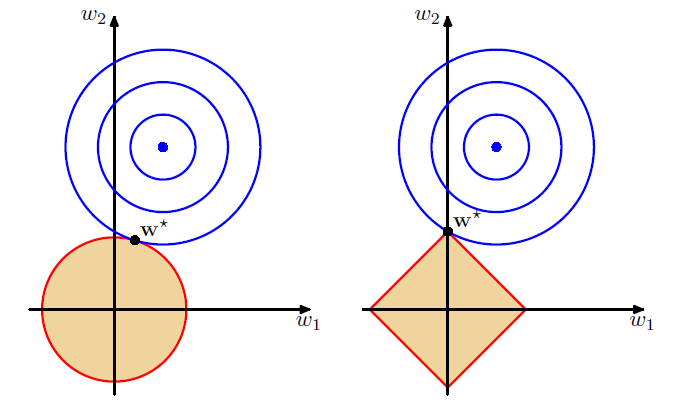
# L2 Norm $\ell_{2}$ in Regularization
L2 Norm 的等高线是圆形的
使用$L_2$范数的一个原因是它对权重向量的大分量施加了巨大的惩罚。 这使得我们的学习算法偏向于在大量特征上均匀分布权重的模型。 在实践中,这可能使它们对单个变量中的观测误差更为稳定。1
使用L2正规化在训练时"更稳定".
# L1 Norm $\ell_{2}$ in Regularization
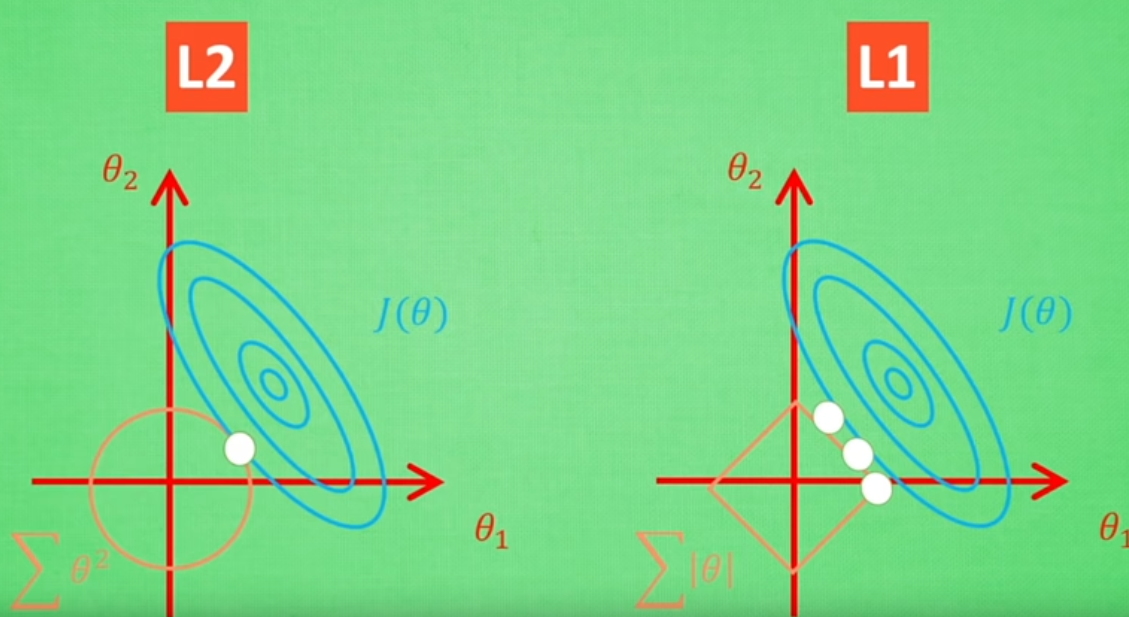
L1 Norm的等高线是方形的, 在正方形上面每一点的取值相同.
L1 范数形状更"尖锐", 从图形中可以看出正方形的四个角都在坐标轴上, 这使得L1范数找到的"平衡点"很可能将权重集中在一小部分特征上, 而将其他权重清除为零, 也就是说, L1范数约束后的解很"稀疏", 这在特征选择时是很有用的
- 这个视频将L1范数与稀疏性的关系讲的很好:
# L1 L2 范数约束下的线性回归: LASSO回归 与 岭回归
线性回归加上L2范数进行正则化就是岭回归, 岭回归通常在样本特征之间相关性很高的时候使用, “让参数的方差变小”, 获得比较稳定的解.
线性回归加上L1范数进行正则化则叫做LASSO回归(Least Absolute Shrinkage and Selection Operator, 套索回归), LASSO的主要思想是构造一个一阶惩罚函数获得一个精炼的模型, 通过最终确定一些变量的系数为0进行特征筛选。3
下面的文章可以进一步了解这两种方法: