D2L-44-Batch_Normalization-批量归一化

Last updated Mar 5, 2022 Edit Source

• All
• Batch normalization
• Normalization
• Deep learning
• Regularization

Tags: #BatchNormalization #Normalization #DeepLearning #Regularization

• 批量归一化是一种加速收敛的方法.

• 批量归一化作用于每一个mini-Batch, 先将这个Batch归一化, 然后再做一个统一的偏移与拉伸.

  • 最后这个偏移和拉伸的量是一个可以学习的超参数

• 对于全连接层, BN作用于每一个特征

• 对于卷积层, BN作用于每一个通道.

• 虽然BatchNorm效果很好, 但其实Batch Normalization效果好的原因并不明朗, 下面的原因也都是事后的推测.

• 原作者认为Batch Norm能够减少网络内部的"协变量偏移", 也就是说网络内部的特征分布可能发生变化. BatchNorm能够减弱这种变化

• 但是且不说作者误用了"协变量偏移"这个词, 一些研究表明Batch Norm并没有改变网络内部的变量分布, 而是使损失函数更加平滑了.

• 从权重稳定性的角度则可以这样理解:

BN层可以作用在全连接层或者卷积层的输出之前和输入之后, 并且在激活函数之前.

• 对于全连接层, BN作用于每一个特征 $$\mathbf{h}=\phi(\mathbf{B N}(\mathbf{W} \mathbf{x}+\mathbf{b}))$$

• 对于卷积层, BN作用于每一个通道.

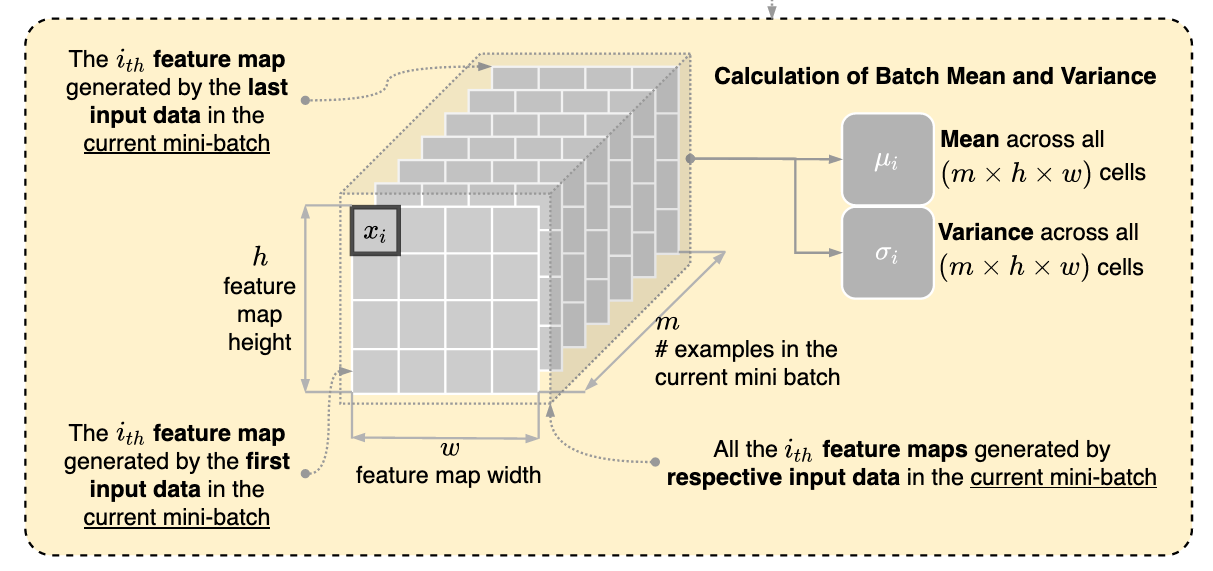
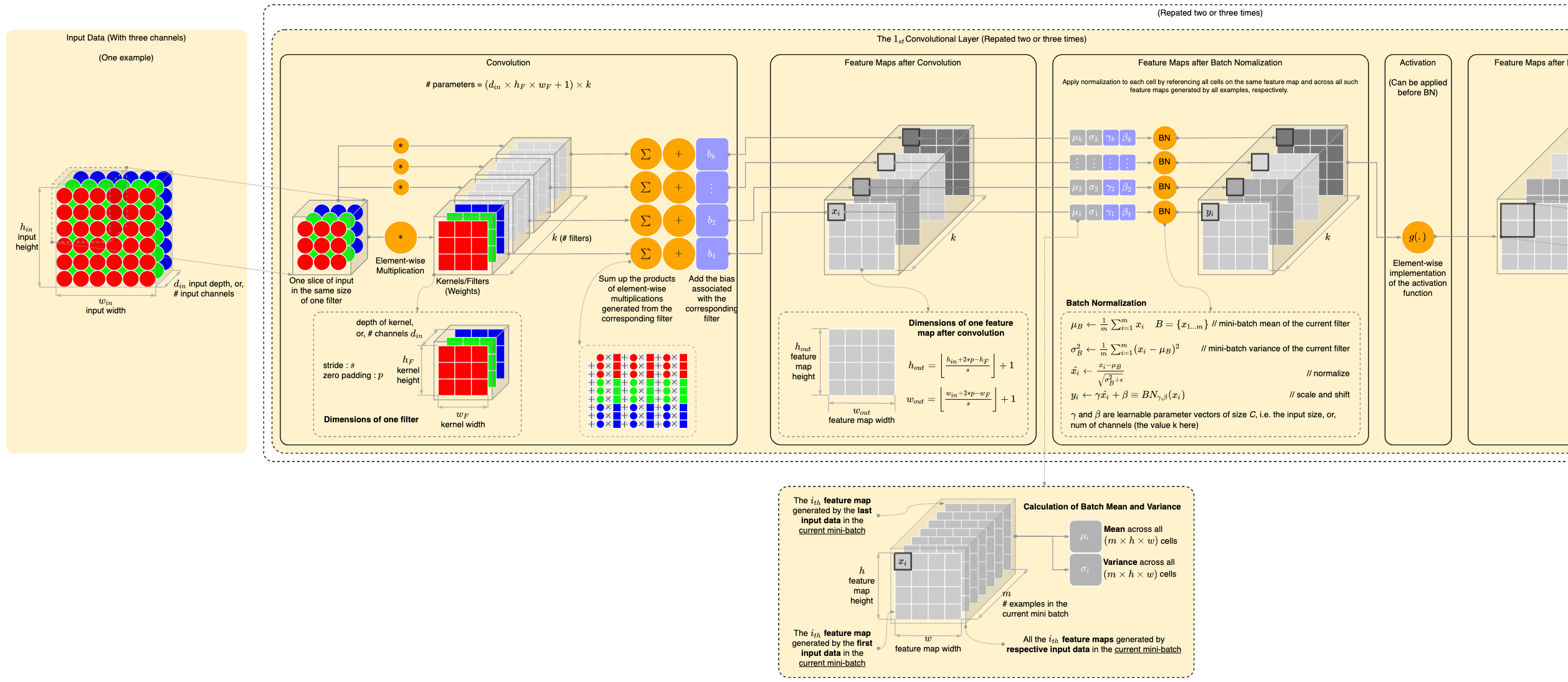
• 也就是说, 假设每一个Batch有 $n$ 个样本 $X_1, X_2, \cdots, X_n$, 这些样本经过卷积之后得到 $n$ 个输出 $O_1, O_2, \cdots, O_n$, 每一个输出有 $c$ 个通道 $O_i^{(1)}, O_i^{(2)}, \cdots, O_i^{(c)}$, 通道的大小为 $h\times w$

• BatchNorm将每一个输出 $O_i$ 里面的第 $k$ 个通道 $O_i^{(k)}$ 取出来, 全部展开拉成一条向量(Flatten), 里面一共有 $n\times h\times w$ 个元素 , 然后计算这个长条所有元素的平均值 $\mu_k$ 和方差 $\sigma_k$.

  • 接下来用均值 $\mu_k$ 和方差 $\sigma_k$ 对每一个元素进行归一化.
  • 进一步, 利用参数 $\beta_k$ 和 $\gamma_k$ 对所有元素进行拉伸和平移.
  • 最后将所有元素拼成原来的形状, 塞回原来的位置¹

  ²

• 每一个通道对应一对 $\beta_k$ 和 $\gamma_k$ , $\beta_k$ 和 $\gamma_k$ 都是可以学习的参数.

• 从形式上来说, 用 $\mathbf{x} \in \mathcal{B}$ 表示一个来自小批量 $\mathcal{B}$ 的输入，批量规范化BN对 $\mathbf{x}$ 的作用可以表示为: $$\operatorname{BN}(\mathbf{x})=\gamma \odot \frac{\mathbf{x}-\hat{\boldsymbol{\mu}}{\mathcal{B}}}{\hat{\boldsymbol{\sigma}}{\mathcal{B}}}+\boldsymbol{\beta}$$

  • 上式中 $\hat{\boldsymbol{\mu}}{\mathcal{B}}$ 是小批量 $\mathcal{B}$ 的样本均值, $\hat{\boldsymbol{\sigma}}{\mathcal{B}}$ 是小批量 $\mathcal{B}$ 的样本标准差。
  • 应用标准化后, 生成的小批量的平均值为 0 和单位方差为 1 。
  • 将输出进行这样的标准化是一个比较强的约束, 这并不总是合理的, 因此我们通常包含 拉伸参数（scale） $\gamma$ 和偏移参数（shift） $\boldsymbol{\beta}$, 它们的形状与 $\mathbf{x}$ 相同。
  • 请注意, $\gamma$ 和 $\boldsymbol{\beta}$ 是需要与其他模型参数一起学习的参数。

• 请注意，如果我们尝试使用大小为1的小批量应用批量规范化，我们将无法学到任何东西。 这是因为在减去均值之后，每个隐藏单元将为0。 所以，只有使用足够大的小批量，批量规范化这种方法才是有效且稳定的。 请注意，批量大小的选择在有BN时比没有BN时更重要。

• 每一个批量的均值 $\hat{\boldsymbol{\mu}}{\mathcal{B}}$ 和方差 $\hat{\boldsymbol{\sigma}}{\mathcal{B}}$ 的计算如下所示: $$\begin{aligned} \hat{\boldsymbol{\mu}}{\mathcal{B}} &=\frac{1}{|\mathcal{B}|} \sum{\mathbf{x} \in \mathcal{B}} \mathbf{x} \\ \hat{\boldsymbol{\sigma}}{\mathcal{B}}^{2} &=\frac{1}{|\mathcal{B}|} \sum{\mathbf{x} \in \mathcal{B}}\left(\mathbf{x}-\hat{\boldsymbol{\mu}}_{\mathcal{B}}\right)^{2}+\epsilon \end{aligned}$$

  • 请注意, 我们在方差估计值中添加一个小的常量 $\epsilon>0$, 以确保即使方差很小, 我们也永远不会除以零。
  • 估计值 $\hat{\boldsymbol{\mu}}{\mathcal{B}}$ 和 $\hat{\boldsymbol{\sigma}}{\mathcal{B}}$ 与Batch的随机性密切相关, 也就是说, 在对输入进行归一化的同时其实是会引入噪声的, 。你可能会认为这种噪声是一个问题, 而事实上它是有益的。
    • This turns out to be a recurring theme in deep learning. For reasons that are not yet well-characterized theoretically, various sources of noise in optimization often lead to faster training and less overfitting: this variation appears to act as a form of regularization. In some preliminary research, Teye et al., 2018 and Luo et al., 2018 relate the properties of batch normalization to Bayesian priors and penalties respectively. In particular, this sheds some light on the puzzle of why batch normalization works best for moderate minibatches sizes in the 50∼100 range.³

• 这里面N是样本的个数, D是特征数

• 训练的时候是以Batch进行的, 而预测的时候我们通常输入的是单张图片, 那我们怎么计算均值和方差呢?
  • 我们使用训练样本整体的均值和方差来代替