D2L-45-ResNet

Last updated Mar 6, 2022 Edit Source

• All
• Res net
• Cnn
• Deep learning

Tags: #ResNet #CNN #DeepLearning

• ResNet在网络中引入了残差连接的思想, 简单的改变带来了很棒的效果.

• 残差连接让每一层很容易地包含了原始函数¹, 这样能保证新增加的每一层都能包含原来的最优解, 进一步在原来的基础上继续改进.

• 我们定义 $\mathcal{F}$ 是某个模型能够拟合的所有函数构成的函数类. 即对于 $\forall f\in \mathcal{F}$, 都存在一组参数使得模型能够拟合到 $f$.

• 假设对于某个问题存在最优的函数 $f^*$.

  • 如果 $f^*\in\mathcal{F}$, 那么网络很容易就能找到最优解.
  • 但是生活总是充满了艰辛, 我们通常都只能委曲求全, 在 $\mathcal{F}$ 里面寻找一个最优近似 $f^*_{\mathcal{F}}$.

• 形式化的说, 我们训练网络的过程就是在寻找: $$f_{\mathcal{F}}^{*} \stackrel{\text { def }}{=} \underset{f}{\operatorname{argmin}} L(\mathbf{X}, \mathbf{y}, f) \text { subject to } f \in \mathcal{F}$$

  • 其中 $L$ 是损失函数.

• 为了找到更好的近似解, 我们需要改进我们的模型: $\mathcal{F}\rightarrow \mathcal{F}’$. 但是新的近似解 $f^*_{\mathcal{F’}}$ 总是更好的吗?

  • 要是 $\mathcal{F}\notin \mathcal{F}’$, 那么新的解可能还不如原来的解. 就像上图中表示的那样: 我们不断地改进模型, 函数类却离最优解越来越远, 模型的表现越来越差.

  • 为了保证我们能够脚踏实地向着目标前进, 我们就必须要保证 $\mathcal{F}\in \mathcal{F}’$, 这样每一步都是在前一次最好结果的基础上改进的.

    • 加了一层网络, 即使没有变好, 但至少不会变差.

• 怎么让 $\mathcal{F}\in \mathcal{F}’$ 呢? 我们可以让新的结构尽可能简单地包含原始函数, 或者说要让新的函数很容易变成恒等映射.

  • 最简单的方法就是让网络能够直接跳过新的结构 $f(\mathbf{x})$
  • 也就是说, 让网络的输出 $g(\mathbf x)=f(\mathbf{x})+\mathbf{x}$. 这样只需要让新结构 $f(\mathbf{x})$ 的参数变成0, 就能恢复原来网络的表达能力. 这就是构建Residual Block的基本直觉.

• 现在让我们从另一个角度来考虑残差连接的有效性.
• 一昧的加深神经网络并不能带来模型性能的提升. 这有时候是因为 模型容量 与数据集不匹配导致了 过拟合, 有时则是因为过深的网络造成了梯度爆炸或者梯度消失的问题.
  • 对于 后一种问题, 谨慎地初始化参数可能会有一些帮助, 但是这并不能从根本上解决问题. 而残差连接提供了一种新的思路: 用加法代替乘法.²
• 为了简单起见, 我们将靠近输入的网络抽象为 $f(\mathbf x)$, 靠近输出的网络表示为 $g(\mathbf x)$.
  • 如果我们将前一层网络的输出作为下一层网络的输入, 则模型表示为 $$g\left(f(\mathbf x)\right)$$
  • 嵌套网络在 $f(\mathbf x)$ 层的梯度为: $$\begin{aligned} \frac{\partial}{\partial\mathbf{w}}g\left(f(\mathbf x)\right)&=\frac{\partial g\left(f(\mathbf x)\right)}{\partial f(\mathbf x)}\frac{\partial f(\mathbf x)}{\partial \mathbf w} \end{aligned}$$
    • 因为梯度是反向传播的, 如果网络比较深, 这个梯度会因为矩阵连乘变得较小³ . 这进一步会导致网络深层的更新较慢, 甚至因为梯度消失而不收敛.
    • 下图是论文里面提供的一个例子. 可以看到更深的网络的训练误差和测试误差都更高, 这说明网络"学不动了".
• 我们来看看残差链接是怎样解决这个问题的, 对于含残差连接的网络, 可以形象化的表示为 $$g(\left(f(\mathbf x)\right) +f(\mathbf x)$$
  • 这个网络在 $f(\mathbf x)$ 层的梯度为: $$\begin{aligned} \frac{\partial}{\partial\mathbf{w}}\left(g\left(f(\mathbf x)\right)+f(\mathbf x)\right)&=\frac{\partial g\left(f(\mathbf x)\right)}{\partial \mathbf w}+\frac{\partial f(\mathbf x)}{\partial \mathbf w} \end{aligned}$$
    • 尽管前面那部分依然有梯度消失的问题, 但是后面的 $\frac{\partial f(\mathbf x)}{\partial \mathbf w}$ 依然能保证训练的继续进行.

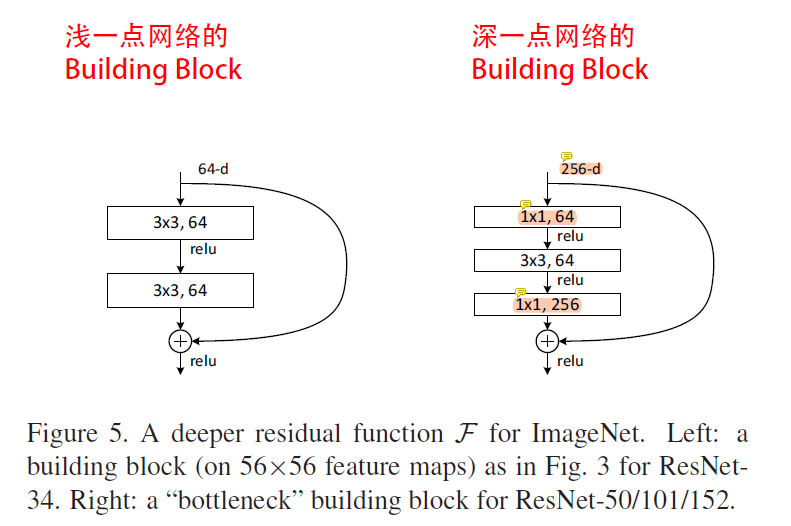
• 遵循上面的设计思路, ResNet残差块的基本结构如上所示

• ResNet沿用了VGG完整的 $3×3$ 卷积层设计。 残差块里首先有2个有相同输出通道数的 $3×3$ 卷积层。 每个卷积层后接一个批量归一化层(BN)和ReLU激活函数。

• 残差通路(Shortcut) 则跳过这2个卷积运算，将输入直接加在最后的ReLU激活函数前。

  • 因为需要将卷积后的输出与残差通路相加, 所以这样的设计要求卷积层的输入输出形状一样。
  • 如果想改变通道数，就需要引入一个额外的 $1×1$ 卷积层来将输入变换成需要的形状后再做相加运算。
  • 残差块的实现如下：

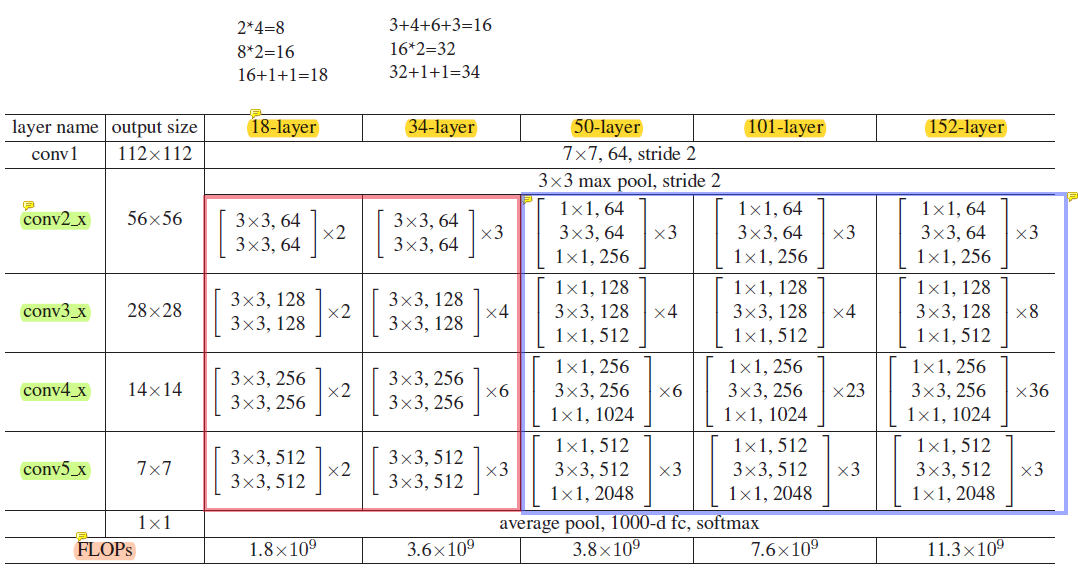
• ResNet遵循了VGG的模块思想, 并且进一步为不同规模的模型构建了两种不同的Building Block: ⁴
  • 深层的网络输入通道会更多, 因此ResNet先利用 $1\times1$ 的卷积将输入通道进行融合, 在卷积后再还原原来的通道数目.⁵
  • 下图是不同规模ResNet的基本架构, 可以看出50层往上的ResNet都采用了第二种架构. ⁴

• GoogLeNet在后面接了4个由Inception块组成的模块。 ResNet则使用4个由残差块组成的模块，每个模块使用若干个同样输出通道数的残差块。
• 更详细的模型实现参见教材(ResNet18): 7.6. 残差网络（ResNet） ResNet模型