D2L-48-序列模型-Sequence_Models

Last updated Mar 7, 2022 Edit Source

• All
• Sequence model
• Sequential data

Tags: #SequenceModel #SequentialData

• 两种流行的序列模型是自回归模型和隐变量自回归模型

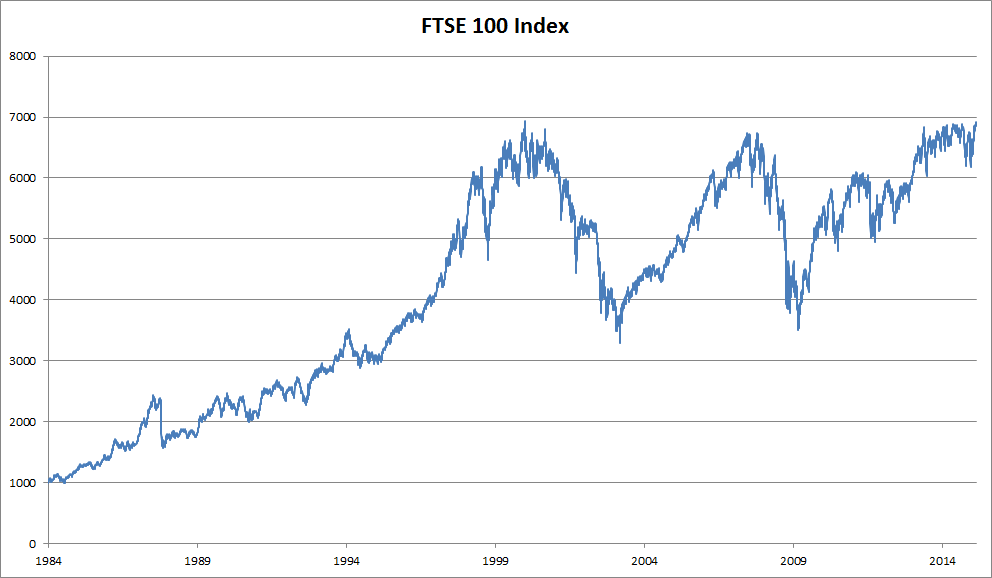
• 假设我们想要根据前 $t-1$ 天的股票价格预测今天的股票价格 $x_t$, 这个问题可以抽象为： $$x_{t} \sim P\left(x_{t} \mid x_{t-1}, \ldots, x_{1}\right)$$

  • 问题的关键在于估计 $P\left(x_{t} \mid x_{t-1}, \ldots, x_{1}\right)$

• 一个简单的想法是使用回归模型来估计概率。但是我们首先需要解决这么一个问题： 随着时间的流逝，模型的输入 $x_1, \cdots，x_{t-1}$ 会不断增加，计算会变得越来越困难，直到不可接受。

• 基于不同的假设，我们得到了两种模型：自回归模型 和 隐变量自回归模型

• 自回归模型的假设是： 只有最近一段时间的数据是有用的，这被称为马尔可夫条件(Markov condition)。因此，我们只需要考虑一个时间跨度 $\tau$ 里面的所有数据: $x_{t-1}, \ldots, x_{t-\tau}$.

  • 因为输入的长度是不变的，所以模型的参数也是不变的.

• 因为模型根据 $x_{t-1}, \ldots, x_{t-\tau}$ 预测 $x_t$, 相当于是在对变量 $x$ 自身进行回归. 故称模型为"自回归模型".

• 如果将模型表示为 $f(x)$, 则自回归模型可以抽象为: $$p\left(x_{t} \mid x_{t-1}, \ldots x_{1}\right)=p\left(x_{t} \mid x_{t-1}, \ldots, x_{t-\tau}\right)=p\left(x_{t} \mid f\left(x_{t-1}, \ldots, x_{t-\tau}\right)\right)$$

• 满足马尔可夫条件的模型称为马尔可夫模型(Markov Model). 根据 $\tau$ 的不同取值, 我们可以得到不同"阶数"的模型:
  • $\tau=1$ : 一阶马尔可夫模型 $$P\left(x_{1}, \ldots, x_{T}\right)=\prod_{t=1}^{T} P\left(x_{t} \mid x_{t-1}\right) \text { 当 } P\left(x_{1} \mid x_{0}\right)=P\left(x_{1}\right)$$
    • 当 $x_i$ 取离散值的时候, 一阶马尔可夫模型可以使用动态规划可以沿着马尔可夫链精确地计算结果. 比如: $$\begin{aligned} P\left(x_{t+1} \mid x_{t-1}\right) &=\frac{\sum_{x_{t}} P\left(x_{t+1}, x_{t}, x_{t-1}\right)}{P\left(x_{t-1}\right)} \\ &=\frac{\sum_{x_{t}} \textcolor{red}{P\left(x_{t+1} \mid x_{t}, x_{t-1}\right)} P\left(x_{t}, x_{t-1}\right)}{P\left(x_{t-1}\right)} \\ &=\sum_{x_{t}} \textcolor{red}{P\left(x_{t+1} \mid x_{t}\right)} P\left(x_{t} \mid x_{t-1}\right) \end{aligned}$$
    • 红色的部分利用了马尔可夫条件, 我们不需要考虑 $x_{t-1}$ 即可求得结果.

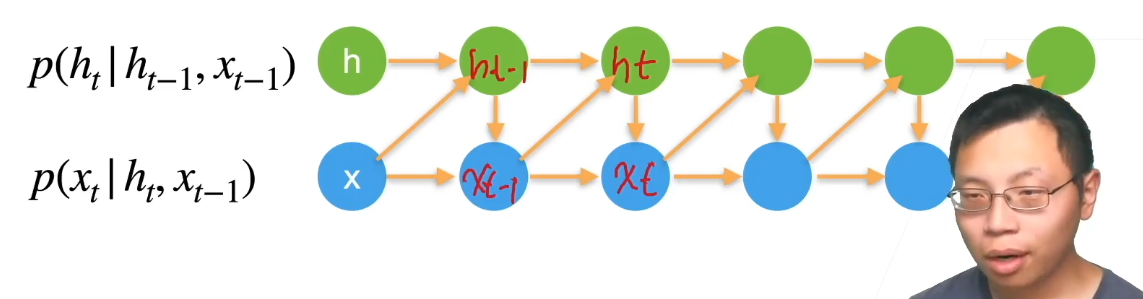
• 这个模型的假设是: “之前所有输入都可以总结为隐变量 $h_{t}$ “, 我们可以根据隐变量来预测 $x_t$

  • 如上图所示, 我们保留一些对过去观测的总结 $h_{t}$ , 同时更新预测 $\hat{x}{t}$ 和总结 $h{t}$ 。也就是基于 $\hat{x}{t}=P\left(x{t} \mid h_{t}\right)$ 来估计 $x_{t}$ .

• 有时也可以写成这样: 根据上一次输出与潜变量一起决定这一次的输出.

• 假设上面的模型能够成功地预测股价, 我们的模型到底学到了什么呢?
  • 模型的输出是在不断地变化的, 而我们的模型学习到的应该是这种变化背后的规律(Dynamics). 如果这个规律不会变化, 我们就称其为"静止的"规律 (Dynamics, 动力学).

• 我们可以这样表示一个序列的总概率: $$P\left(x_{1}, \ldots, x_{T}\right)=\prod_{t=1}^{T} P\left(x_{t} \mid x_{t-1}, \ldots, x_{1}\right)$$ ^973ecf
• 但是, 数学上我们完全也可以反过来写: $$P\left(x_{1}, \ldots, x_{T}\right)=\prod_{t=T}^{1} P\left(x_{t} \mid x_{t+1}, \ldots, x_{T}\right)$$

  • 但是这意味着现在的事件影响了过去的事件! 但是这有意义吗?

  • 在许多情况下，数据存在一个自然的方向，即在时间上是前进的。 很明显，未来的事件不能影响过去。 因此，如果我们改变 $x_t$，可能会影响未来发生的事情 $x_{t+1}$ ，但不能反过来。也就是说，如果我们改变 $x_t$ ，基于过去事件得到的分布不会改变。 因此，解释P $(x_{t+1}∣x_t)$ 应该比解释 $P(x_t∣x_{t+1})$ 更容易。 ^f8bb86

    • 例如，在某些情况下，对于某些可加性噪声 $ϵ$， 显然我们可以找到 $x_{t+1}=f(x_t)+ϵ$， 而反之则不行 Hoyer et al., 2009。 这是个好消息，因为这个前进方向通常也是我们感兴趣的方向。

• 对于直到时间步 $t$ 的观测序列，其在时间步 $t+k$ 的预测输出是“ $k$ 步预测”。
• 例如5步预测可以表示如下: $$\begin{aligned} &\textcolor{blue}{\hat{x}{5}}=f\left(x{1}, x_{2}, x_{3}, x_{4}\right) \\ &\textcolor{blue}{\hat{x}{6}}=f\left(x{2}, x_{3}, x_{4}, \textcolor{blue}{\hat{x}{5}}\right) \\ &\textcolor{blue}{\hat{x}{7}}=f\left(x_{3}, x_{4}, \textcolor{blue}{\hat{x}{5}}, \textcolor{blue}{\hat{x}{6}}\right) \\ &\textcolor{blue}{\hat{x}{8}}=f\left(x{4}, \textcolor{blue}{\hat{x}{5}}, \textcolor{blue}{\hat{x}{6}}, \textcolor{blue}{\hat{x}{7}}\right) \\ &\textcolor{blue}{\hat{x}{9}}=f\left(\textcolor{blue}{\hat{x}{5}}, \textcolor{blue}{\hat{x}{6}}, \textcolor{blue}{\hat{x}{7}}, \textcolor{blue}{\hat{x}{8}}\right) \end{aligned}$$
• 但是随着我们对预测时间 $k$ 值的增加，会造成误差的快速累积和预测质量的急速下降。